Содержание
Введение……………………..…………………………….……………..……3
1.Определение реакций опор твёрдого тела……………………………..….3
2.Смета на строительство дачного дома………………………….……7
3. Численное интегрирование функций методом трапеций ………...…….7
4.Численное интегрирование функций методом Симпсона…………...……….9
5.Определение реакций опор пространственного стержня………..……...10
6.Расчёт плоской фермы……………..…………………………………......13
7.Определение характеристик плоского движения точки.……………....18
8.Определение отклонений струны методом конечных разностей …….22
ВВЕДЕНИЕ
В настоящее время сколь-нибудь значимые строительные проблемы решаются с помощью численных методов и их реализующих вычислительных комплексов. Для решения современных задач отрасли аналитические методы малоэффективны. К примеру, статический и динамический расчеты десятки и сотни тысяч раз статически неопределимых стержневых систем, расчёты таких сложных конструкций, как тонкие пластины и оболочки, крупные массивы гидротехнических сооружений, планирование и организация деятельности больших строительных концернов, управление возведением крупных строительных объектов.
И, вообще, широкое применение численных математических методов и ЭВМ в различных областях творческой деятельности специалистов, стало совершенно необходимым в настоящее время. Следовательно, тематика задач данной курсовой работы является актуальной.
ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КУРСОВОЙ РАБОТЫ
Курсовая работа по дисциплине «Численные методы и вычислительные комплексы»выполняется в 1-м семестре 2 курса бакалавриата направления подготовки 08.03.01 – Строительство и содержит восемь задач, выбираемых из данного пособия.
Определение реакций опор твёрдого тела.
2. Смета на строительство дачного дома.
3. Численное интегрирование функций методом трапеций.
4.Численное интегрирование функций методом Симпсона.
5. Определение реакций опор пространственного стержня.
6. Расчёт плоской фермы.
7. Определение характеристик плоского движения точки.
8. Определение отклонений струны методом конечных разностей.
Листинг решения в табличном процессоре EXCEL
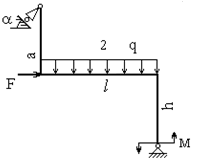
Определение реакций опор твёрдого тела
Задана схема бруса c ломанной осью. Брус нагружен сосредоточенной
силой F, распределённой нагрузкой интенсивностью q
и парой сил с моментом М. Численные значения нагрузок и размеров
берутся из таблицы. Определить реакции опор с помощью табличного EXCEL
Исходные данные
Шифр
F
α
кН
град.
5,0
50
Исходная схема
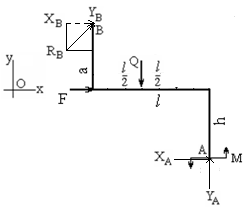
Расчётная схема
Решение
Сосредоточенная сила
Q = 2ql = 12.8 кН
RB разлагается на компоненты XB, YB
ХB= RB cosα, YB = RB sinα.
Уравнения равновесия
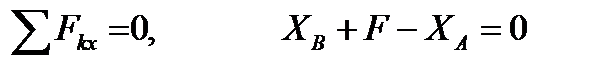 .
.
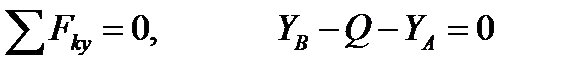 .
.
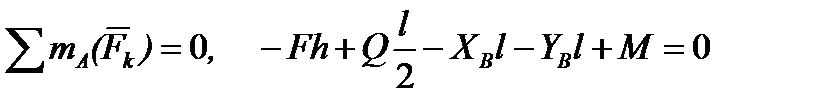 .
.
Опорные реакции. Из уравнения (3) :
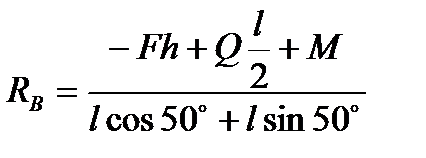 .
.
RB=2,519 кН XB=1,511кН YB=1,763кН
XA=XB=1,511 кН YA= YB - Q = -11,036 кН
Листинг программы
% Решается система алгебраических уравнений АХ=b
Clearall;
tic
disp('начало______________________')
% Исходные данные:
a=1.6; h=2.6; l=3.6; F1=3; F2=6; q=2.8;
n=6; A=zeros(n,n); b=zeros(n,1); X=zeros(n,1);
% Элементыматрицы A
A(1,2)=1; A(1,5)=1; A(2,3)=-1; A(2,6)=1;
A(3,1)=1; A(3,4)=1; A(4,4)=a; A(4,6)=-h;
A(5,5)=h; A(6,5)=-a; A(6,6)=-l;
% Компонентывектораb
b(1)=-F2; b(2)=-q*l; b(3)=F1;
b(4)=F1*a; b(5)=F1*l; b(6)=F1*a;
% Решение системы уравнений: АХ=b
X=A\b
disp('конец_______________________')
toc
>>Zhukov
начало______________________
X =
5.1667
-10.1538
6.9005
-2.1667
4.1538
-3.1795
конец_______________________
Elapsed time is 0.000191 seconds.
Расчёт плоской фермы
Плоская ферма состоит из семи стержней и держится на трёх опорных стержнях (рис. 1). Определить усилия в стержняхс помощью вычислительного комплекса МАТЛАБ.
Исходные данные
| Шифр | а м | h м | F1 кН | F2 кН |
| 19–4 | 2,9 | 3,1 | 7 | 5 |
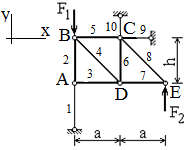
| Исходная схема | Расчётная схема | |
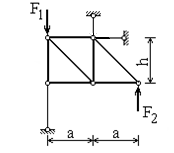
| 
| |
| Рис. 1 | Рис. 2 |
Решение
Ферма и приложенные силы находится в вертикальной плоскости и представляют плоскую систему. Для неё соблюдается условие статической определённости в виде соотношения между количествами стержней, узлов и опорных стержней:
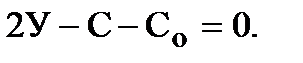
Количество узлов 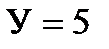 , стержней
, стержней 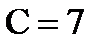 , опорных стержней Co=3. Очевидно, что условие выполняется.
, опорных стержней Co=3. Очевидно, что условие выполняется.
Изобразим расчётную схему (рис. 2). Покажем координатные оси х, у, отметим узлы A, B, C, D, E, B, номера стержней 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
Приступим к определению усилий в стержнях методом вырезания узлов. С этой целью вырежем узлы A, B, C, D, E, B, (рис. 3), обозначим продольные силы в сечениях стержней 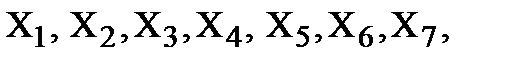
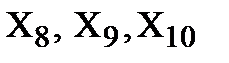 .
.
Необходимые для составления уравнений равновесия углы наклона стержней к к оси x - ов найдём по рис. 2,3:
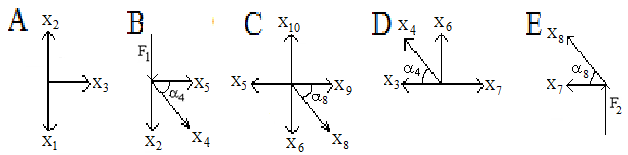
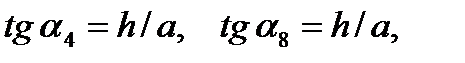
Тригонометрические функции, требующиеся далее при составлении уравнений равновесия, легко определяются по известным формулам их соотношений:

Рассмотрим условия равновесия каждого узла.
Узел A . Предполагая сходящиеся к нему стержни 1 и 2 растянутыми, изобразим узел и силы, приложенные к нему. Составим уравнения равновесия в виде равенства нулю сумм проекций сил на координатные оси x, y:
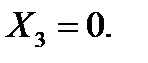 (1)
(1)
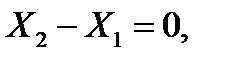 (2)
(2)
Аналогично составляем уравнения равновесия для других узлов:
Узел B .
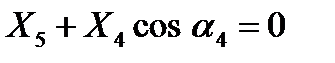 , (3)
, (3)
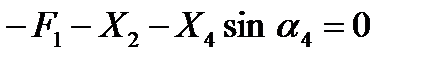 . (4)
. (4)
Узел C .
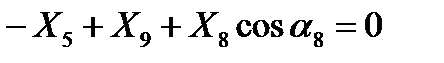 , (5)
, (5)
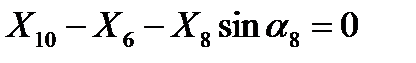 . (6)
. (6)
Узел D .
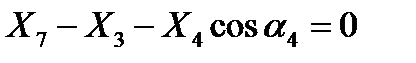 . (7)
. (7)
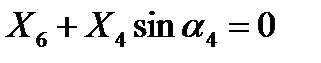 . (8)
. (8)
Узел E .
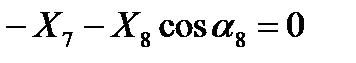 . (9)
. (9)
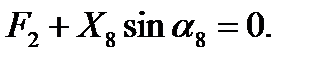 (10)
(10)
Коэффициенты при неизвестных и свободные члены вышеприведённых уравнений (1)- (10) образуют матрицу А и вектор b, cпомощью которых можно найти неизвестные опорные реакции и усилия в стержнях фермы из соответствующей системы алгебраических уравнений
AX = b, (11)
где А – квадратная матрица порядка n=10, b – десятимерный вектор. Выпишем их более наглядно.
A = 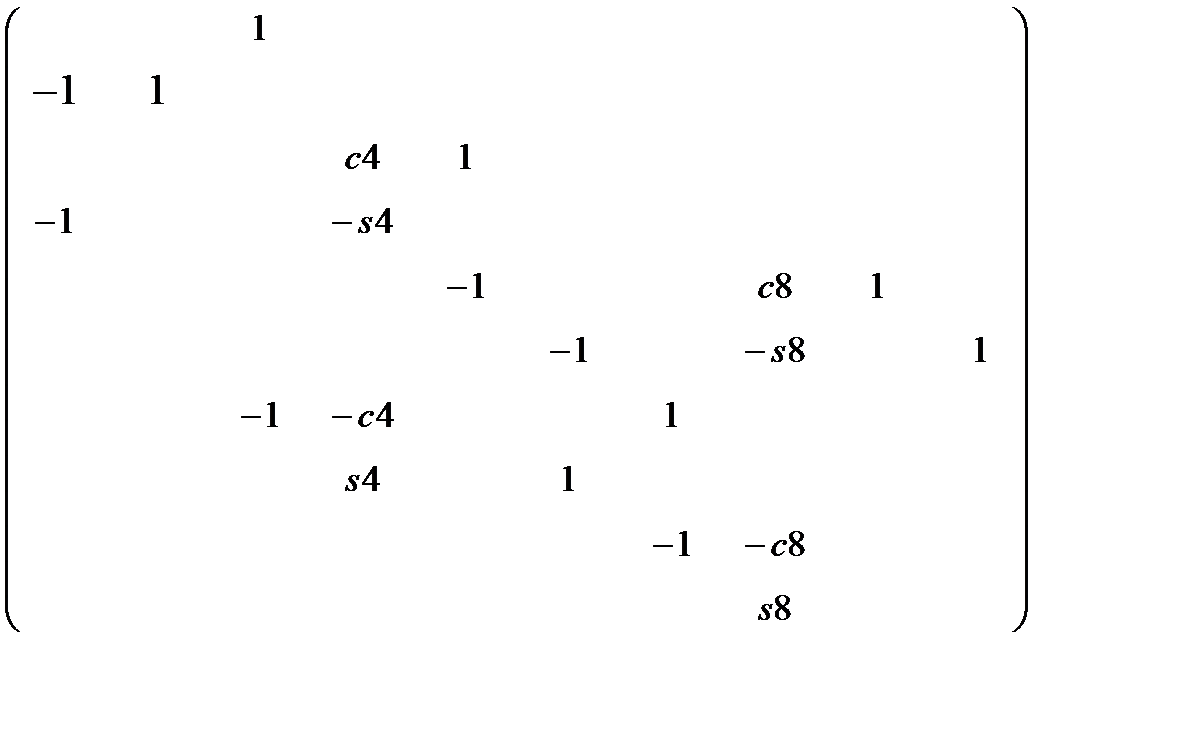 , b=
, b= 
Компьютерная программа на алгоритмическом языке Matlab выдала вектор решения:
X = {-12,0000 -12,0000 0 6,8468
-4,6774 5,0000 4,6774 -6,8468 0 -10,0000} кН.
Отрицательным значениям соответствуют сжатые стержни.
Листинг программы на алгоритмическом языке МАТЛАБ
% Жуков Т.А. Шифр 19-4 30.10.2018
% Расчёт плоской фермы
% Решается система алгебраических уравнений АХ=b
clearall;
tic
disp('начало______________________')
% Исходные данные:
a=2.9; h=3.1; F1=7; F2=5;
n=10; A=zeros(n,n); b=zeros(n,1); X=zeros(n,1);
tg4=h/a;
tg8=h/a;
c4=1/sqrt(1+tg4^2); s4=sqrt(1-c4^2);
c8=1/sqrt(1+tg8^2); s8=sqrt(1-c8^2);
% Элементы матрицы A и вектора b
A(1,3)=1 ; b(4)=F1;
A(2,1)=-1; A(2,2)=1;
A(3,4)=c4; A(3,5)=1;
A(4,2)=-1; A(4,4)=-s4; b(10)=-F2;
A(5,5)=-1; A(5,8)=c8; A(5,9)=1;
A(6,6)=-1; A(6,8)=-s8; A(6,10)=1;
A(7,3)=-1; A(7,4)=-c4; A(7,7)=1;
A(8,4)=s4; A(8,6)=1;
A(9,7)=-1; A(9,8)=-c8;
A(10,8)=s8;
% Решениесистемыуравнений: АХ=b
X=A\b
disp('конец_______________________')
toc
Исходные данные
| Шифр | a м/с | b м | c м/с2 | d м | t1 с |
| 31–6 | 2 | 3 | 4 | 1 | 3/2 |
Решение
После подстановки численных значений уравнения (1) приобретают вид:
x(t) = 2 sin(πt/6) +4, y(t) = 1 cos(πt/6) +3. (2)
Чтобы получить уравнение траектории в координатной форме, части уравнения содержащие sin и cos перенесем в правую части.Возведем обе части уравнений в квадрат и уравнения (2).
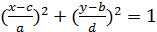 (3)
(3)
Таким образом, получено уравнение эллипсоида.
Положение точки М на траектории в момент времени t1 находим по функциям (2):
x(1,5) = 2·0,8+4 = 5,6 м , y(1,5) = 1  0,5+3 = 3,5 м.
0,5+3 = 3,5 м.
Для построения траектории точки, являющейся кривой линией (часть параболы), необходимо определить положения точки М ещё при нескольких моментах времени вблизи t = t1. Эти вычисления и график выполнены в МАТЛАБ-е. Результаты представлены на рис. 1.
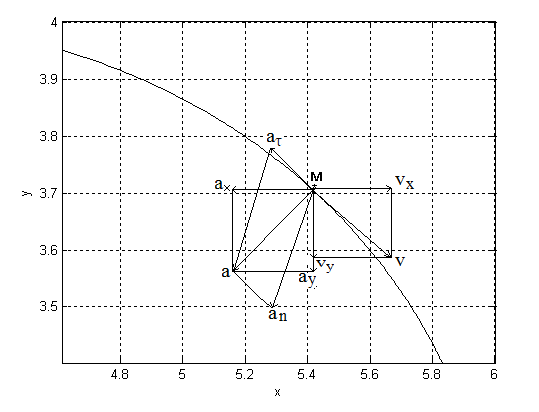
Вычислим проекции скорости и ускорения точки на оси координатvХ, vy, ax, ay, дифференцируя по времени уравнения движения (1):
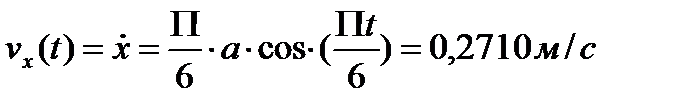 ,
, 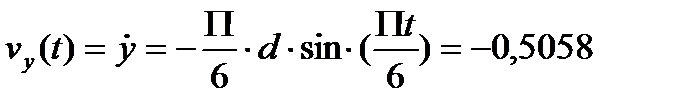 ,
,
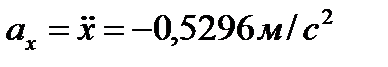 ,
, 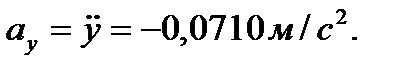
По найденным проекциям определяются модуль скорости:
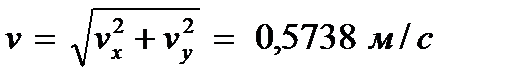
и модуль ускорения точки вычисляется по формуле:
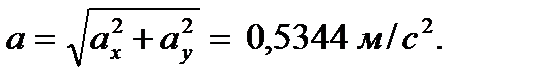
Касательное ускорение точки
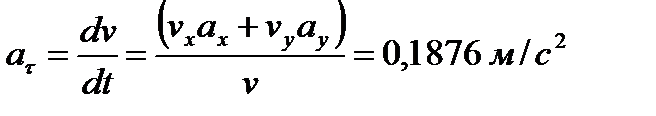 .
.
Полученный знак + означает, что движение точки ускоренное, направления 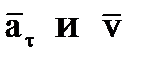 совпадают.
совпадают.
Модуль нормального ускорения точки определяется по формуле:
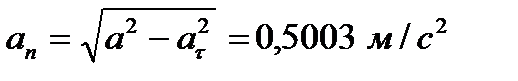 .
.
После того, как найдено нормальное ускорение, радиус кривизны траектории в рассматриваемой точке определяется из выражения:

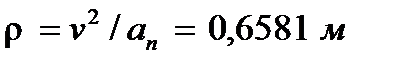 .
.
На рисунке показано положение точки М в заданный момент времени. Векторы скоростей и ускорений наносятся на рис. 1 вручную по их значениям, найденным выше, соблюдая масштабные соотношения между их компонентами.Вектор  строим по составляющим
строим по составляющим 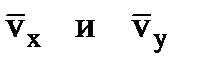 , причём этот вектор должен по направлению совпадать с касательной к траектории. Вектор
, причём этот вектор должен по направлению совпадать с касательной к траектории. Вектор 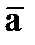 строим по составляющим
строим по составляющим 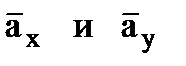 и затем раскладываем на составляющие
и затем раскладываем на составляющие 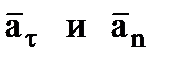 . Совпадение величин
. Совпадение величин 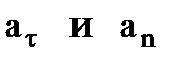 , найденных из чертежа, с их значениями, полученными аналитически, служит контролем правильности решения.
, найденных из чертежа, с их значениями, полученными аналитически, служит контролем правильности решения.
% Жуков Т.А. Шифр 19-4 07.12.18
% Плоское движение точки. Задача 6
% Строит график траектории при x=at+b, y=dt^2+c
% Звёздочкой отмечает на графике положение точки при t=t1
clearall;
tic
disp('начало______________________')
% Исходные данные:
a=2; b=3; c=4; d=1; t1=3/2;
x1=a*sin(pi*t1/6)+c; y1=d*cos(pi*t1/6)+b; % координатыточкиМ
dt=0.01; % шаг построения графика;
D1=t1-1; D2=t1+1;
n=round((D2-D1)/dt);
x=zeros(n+1); y=zeros(n+1); i=1;
for t=D1:dt:D2;
x(i)=a*sin(pi*t/6)+c; y(i)=d*cos(pi*t/6)+b;
i=i+1;
end;
plot(x,y,'k'); grid; % вывод графика на монитор
text(x1,y1,'*') % Точка М на графике
% Скорости и ускорения
xlabel('x'); ylabel('y');
vx=pi/6*a*cos(pi*t/6), vy=-pi/6*d*sin(pi*t/6), v=sqrt(vx^2+vy^2),
ax=-pi^2/36*a*sin(pi*t/6), ay=-pi^2/36*d*cos(pi*t/6), a=sqrt(ax^2+ay^2),
atau=(vx*ax+vy*ay)/v,
an=sqrt(a^2-atau^2),
% Радиускривизны
ro=v^2/an,
disp('конец_______________________')
toc
>> timur1
начало______________________
vx =
0.2710
vy =
-0.5058
v =
0.5738
ax =
-0.5296
ay =
-0.0710
a =
0.5344
atau =
0.1876
an =
0.5003
ro =
0.6581
конец_______________________
Elapsed time is 0.244205 seconds.
>>
Методом конечных разностей
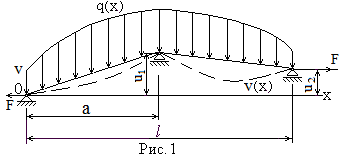 Гибкая струна(рис. 1)лежит на трёх опорах, находящихся на разных уровнях к горизонту, туго натягивается
Гибкая струна(рис. 1)лежит на трёх опорах, находящихся на разных уровнях к горизонту, туго натягивается
продольной силой F, постоянной по всей длине, нагружена неравномерной распределённой нагрузкой
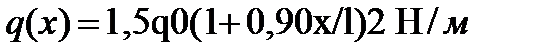
Её изогнутая ось описывается обыкновенным дифференци-альным уравнением второго порядка

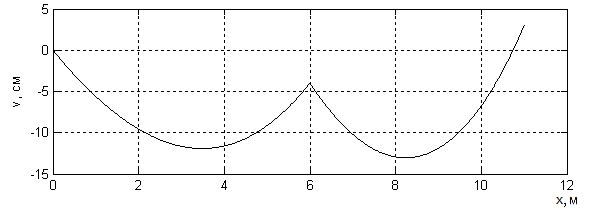
Требуется найти методом конечных разностей сеточную функцию v(xi) и изобразить её график.
Исходные данные
| Второе число шифра | A, см2 | l,м | a, м | σ, МПа | q0, Н/м | u1, см | u2, см |
| 19 - 4 | 0,4 | 11 | 6 | 30 | 11 | -40 | 30 |
Решение
Продольную силу представим в виде
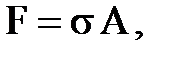
где 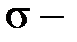 нормальное напряжение в поперечном сечении, А – площадь поперечного сечения. Перепишем (1) в виде
нормальное напряжение в поперечном сечении, А – площадь поперечного сечения. Перепишем (1) в виде
 (1)
(1)
Здесь введено обозначение
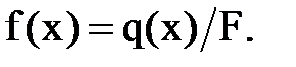
К уравнению (1) присоединяются граничные условия на концах струны
 (2)
(2)
соответствующие факту их неподвижности, и условие на промежуточной опоре
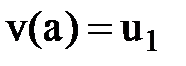 . (3)
. (3)
Задачу (1) - (3) далее будем решать с помощью метода конечных разностей. С этой целью вместо подобласти L + Г введём дискретную область lh в виде узлов равномерной сетки с шагом h
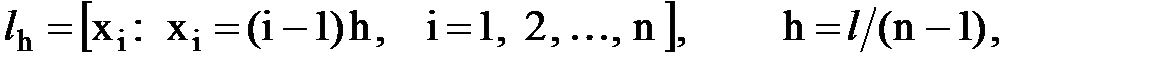
где Г – граница области, n – количество узлов сетки. Значения функций и производной заменим точными и приближёнными значениями в узлах сетки
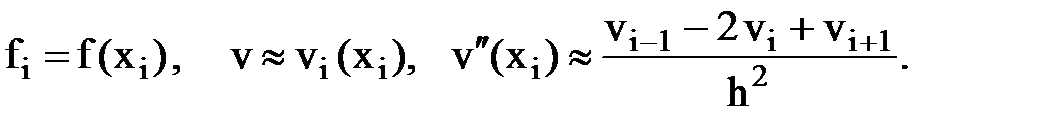
Тогда вместо уравнения (1) и дополнительных условий (2), (3) получим однородную систему линейных алгебраических уравнений
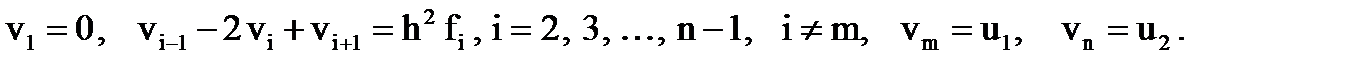
Здесь m – номер точки, совпадающей со средней опорой. Систему уравнений можно переписать в матрично-векторной форме
Bv = с, (6)
где B - квадратная матрица порядка n, vT = {v1, v2,…, vn} – вектор, компонентами которого являются отклонения струны.
Можно легко показать, что матрица коэффициентов является ленточной и трёхдиагональной вида
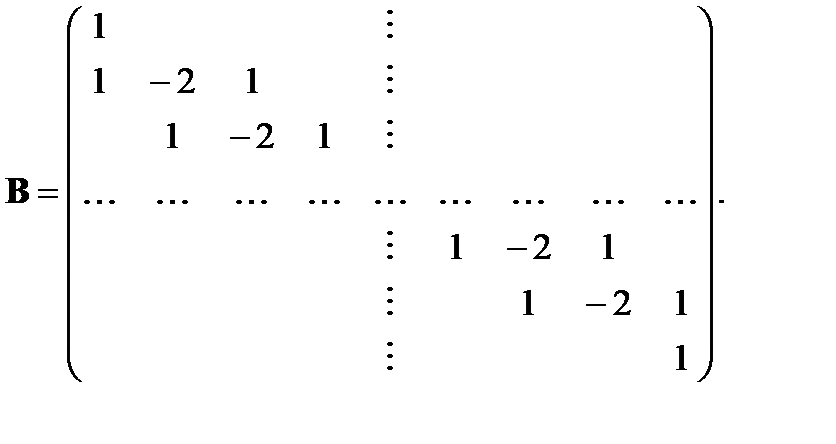
Здесь нулевые элементы не выписаны. Правая часть системы уравнений является вектором
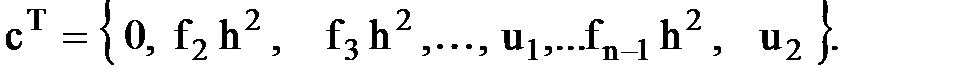
Задача решена с помощью программы на алгоритмическом языке MATLAB. Результаты счёта представлены на рис. 2.
% Струна. Cтатическая задача. 11.12.18
% Отклонения струны. Метод конечных разностей.
% Общая постановка задачи:
% v''=f(x), f(x)=q(x)/sig/A, v(0)=0, v(l)=0.
% Приведение к алгебраической системе общего вида
% B v = c
% и её решение
clearall;
disp ('Начало_____________________')
l=11; a=6; u1=-0.04; u2=0.03; A=0.00004; sig=30e+06;
n=1001; n1=n-1; h=l/n1; m=round(a/h+1);
x=[0 : h : l]; q0=11;
q=1.5*q0*(1+0.90*x/l).^2;
F=sig*A;
f=zeros(1,n); v=zeros(1,n); c=zeros(1,n); B=zeros(n,n);
f=q/F;
% Формирование матрицы В
B(1,1)=1; B(n,n)=1; % Граничные условия
% В регулярных точках сетки
for i=2:m-1;
B(i,i-1)=1; B(i,i)=-2; B(i,i+1)=1; c(i)=f(i)*h^2;
end;
B(m,m)=1; c(m)=u1;
for i=m+1:n-1;
B(i,i-1)=1; B(i,i)=-2; B(i,i+1)=1; c(i)=f(i)*h^2;
end;
c(n)=u2;
% Решение системы уравнений
v=B\c';
plot (x, v*100, 'k','LineWidth',1), grid on;
xlabel('x'); ylabel('v, cм');
disp ('Конец_____________________')
Содержание
Введение……………………..…………………………….……………..……3
1.Определение реакций опор твёрдого тела……………………………..….3
2.Смета на строительство дачного дома………………………….……7
3. Численное интегрирование функций методом трапеций ………...…….7
4.Численное интегрирование функций методом Симпсона…………...……….9
5.Определение реакций опор пространственного стержня………..……...10
6.Расчёт плоской фермы……………..…………………………………......13
7.Определение характеристик плоского движения точки.……………....18
8.Определение отклонений струны методом конечных разностей …….22
ВВЕДЕНИЕ
В настоящее время сколь-нибудь значимые строительные проблемы решаются с помощью численных методов и их реализующих вычислительных комплексов. Для решения современных задач отрасли аналитические методы малоэффективны. К примеру, статический и динамический расчеты десятки и сотни тысяч раз статически неопределимых стержневых систем, расчёты таких сложных конструкций, как тонкие пластины и оболочки, крупные массивы гидротехнических сооружений, планирование и организация деятельности больших строительных концернов, управление возведением крупных строительных объектов.
И, вообще, широкое применение численных математических методов и ЭВМ в различных областях творческой деятельности специалистов, стало совершенно необходимым в настоящее время. Следовательно, тематика задач данной курсовой работы является актуальной.
ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КУРСОВОЙ РАБОТЫ
Курсовая работа по дисциплине «Численные методы и вычислительные комплексы»выполняется в 1-м семестре 2 курса бакалавриата направления подготовки 08.03.01 – Строительство и содержит восемь задач, выбираемых из данного пособия.
Дата: 2018-12-28, просмотров: 482.