Заданы уравнения движения точки М и численные значения параметров к ним. Требуется с помощью вычислительного комплекса МАТЛАБ найти положение точки на траекториидвижения для момента времени t = t1, показать траекторию в окрестности точки. Вычислить скорость, полное, касательное и нормальное ускорения точки М, нанести их на рисунке, определить радиус кривизны траектории.
Заданы уравнения движения точки М:
x(t) = a sin(πt/6) +c; y(t) = d cos(πt/6) +b. (1)
Исходные данные
| Шифр | a м/с | b м | c м/с2 | d м | t1 с |
| 31–6 | 2 | 3 | 4 | 1 | 3/2 |
Решение
После подстановки численных значений уравнения (1) приобретают вид:
x(t) = 2 sin(πt/6) +4, y(t) = 1 cos(πt/6) +3. (2)
Чтобы получить уравнение траектории в координатной форме, части уравнения содержащие sin и cos перенесем в правую части.Возведем обе части уравнений в квадрат и уравнения (2).
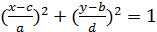(3)
Таким образом, получено уравнение эллипсоида.
Положение точки М на траектории в момент времени t1 находим по функциям (2):
x(1,5) = 2·0,8+4 = 5,6 м , y(1,5) = 1 
0,5+3 = 3,5 м.
Для построения траектории точки, являющейся кривой линией (часть параболы), необходимо определить положения точки М ещё при нескольких моментах времени вблизи t = t1. Эти вычисления и график выполнены в МАТЛАБ-е. Результаты представлены на рис. 1.
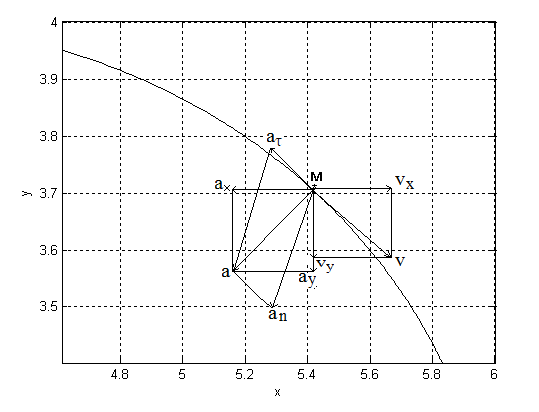
Вычислим проекции скорости и ускорения точки на оси координатvХ, vy, ax, ay, дифференцируя по времени уравнения движения (1):
, 
,
, 
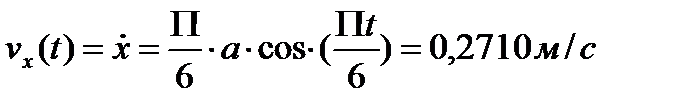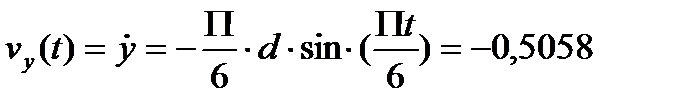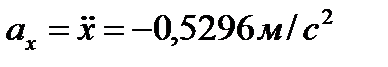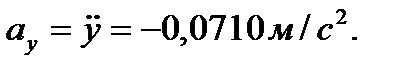
По найденным проекциям определяются модуль скорости:
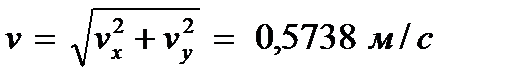
и модуль ускорения точки вычисляется по формуле:
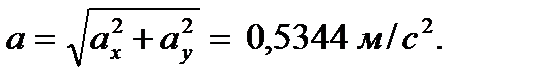
Касательное ускорение точки
.
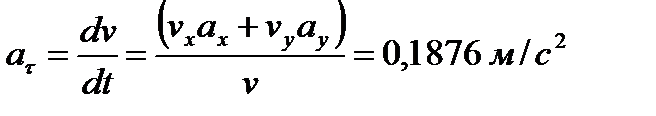Полученный знак + означает, что движение точки ускоренное, направления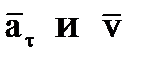 
совпадают.
Модуль нормального ускорения точки определяется по формуле:
.
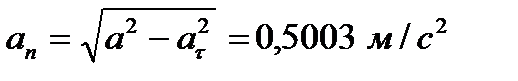После того, как найдено нормальное ускорение, радиус кривизны траектории в рассматриваемой точке определяется из выражения:
.
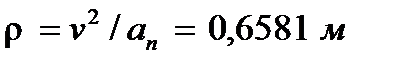На рисунке показано положение точки М в заданный момент времени. Векторы скоростей и ускорений наносятся на рис. 1 вручную по их значениям, найденным выше, соблюдая масштабные соотношения между их компонентами.Вектор 
строим по составляющим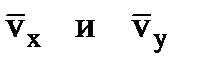 
, причём этот вектор должен по направлению совпадать с касательной к траектории. Вектор 
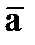строим по составляющим 
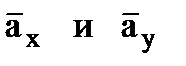и затем раскладываем на составляющие 
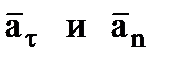. Совпадение величин 
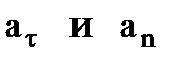, найденных из чертежа, с их значениями, полученными аналитически, служит контролем правильности решения.
% Жуков Т.А. Шифр 19-4 07.12.18
% Плоское движение точки. Задача 6
% Строит график траектории при x=at+b, y=dt^2+c
% Звёздочкой отмечает на графике положение точки при t=t1
clearall;
tic
disp('начало______________________')
% Исходные данные:
a=2; b=3; c=4; d=1; t1=3/2;
x1=a*sin(pi*t1/6)+c; y1=d*cos(pi*t1/6)+b; % координатыточкиМ
dt=0.01; % шаг построения графика;
D1=t1-1; D2=t1+1;
n=round((D2-D1)/dt);
x=zeros(n+1); y=zeros(n+1); i=1;
for t=D1:dt:D2;
x(i)=a*sin(pi*t/6)+c; y(i)=d*cos(pi*t/6)+b;
i=i+1;
end;
plot(x,y,'k'); grid; % вывод графика на монитор
text(x1,y1,'*') % Точка М на графике
% Скорости и ускорения
xlabel('x'); ylabel('y');
vx=pi/6*a*cos(pi*t/6), vy=-pi/6*d*sin(pi*t/6), v=sqrt(vx^2+vy^2),
ax=-pi^2/36*a*sin(pi*t/6), ay=-pi^2/36*d*cos(pi*t/6), a=sqrt(ax^2+ay^2),
atau=(vx*ax+vy*ay)/v,
an=sqrt(a^2-atau^2),
% Радиускривизны
ro=v^2/an,
disp('конец_______________________')
toc
>> timur1
начало______________________
vx =
0.2710
vy =
-0.5058
v =
0.5738
ax =
-0.5296
ay =
-0.0710
a =
0.5344
atau =
0.1876
an =
0.5003
ro =
0.6581
конец_______________________
Elapsed time is 0.244205 seconds.
>>
Дата: 2018-12-28, просмотров: 403.
