Составить уравнения равновесия для пространственной стержневой системы. Определить реакции опор из системы алгебраических уравнений с помощью вычислительного комплекса МАТЛАБ.
Исходные данные:
| Шифр | а м | h м | l м | F1 кН | F2 кН | q кН/м | M |
| 19-4 | 1,6 | 2,6 | 3,6 | 3 | 6 | 2,8 | 11 |
Решение
Исходная схема: Расчетная схема:
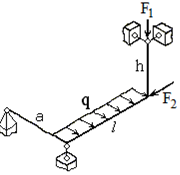
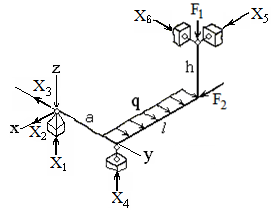
Показываем координатные оси x, y, z, общие для всей расчётной схемы. В шарнирно-неподвижной опоре возникают три опорные реакции X1, X2, X3. Остальные опоры шарнирно-подвижные, поэтому в них возникает по одной опорной реакции: X4, X5, X6. Направления реакций выбираются произвольно. С целью определения реакций опор составим уравнения равновесия всей системы
1) 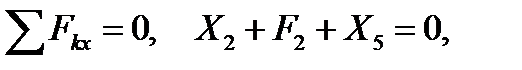
2) 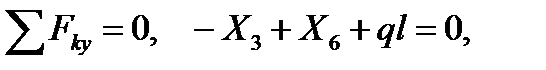
3) 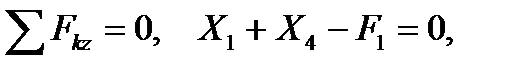
4) 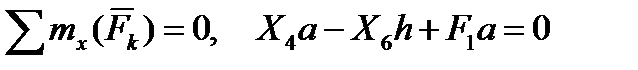 ,
,
5) 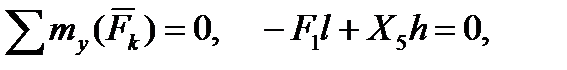
6) 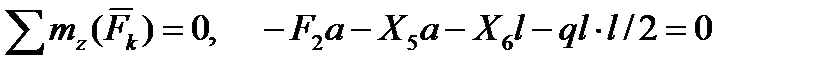 .
.
Уравнения 1)- 6) образуют неоднородную систему линейных алгебраических уравнений, которую представим в матрично-векторной форме
AX = b,
где А – квадратная матрица порядка n=6, X,b – шестимерныйвектор.
A= 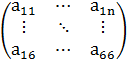 , X =
, X = 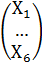 , b =
, b = 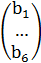 .
.
Ненулевые элементы матрицы А и компоненты вектора bв силу уравнений 1) – 6) имеют вид:
a12=1, a15=1, a23=-1, a26=1, a31=1, a34=1,
a44=a, a46=-h, a55=h, a65=-a, a66=-l;
b1 = -F2, b2=-ql, b3=-F1, b4=F1a b5=-F1l, b6=F2a.
Запишем эти результаты в виде матрицы и вектора более наглядно
A= 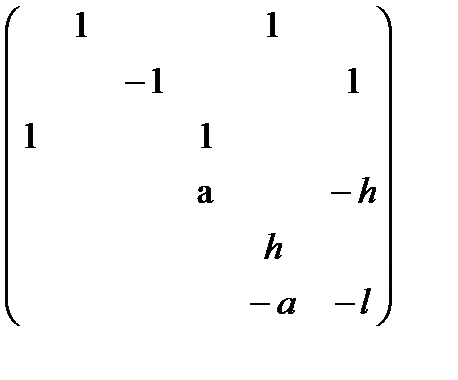 , b=
, b= 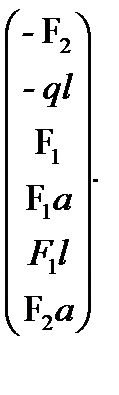
Здесь нулевые элементы не показаны.
Компьютерная программа на алгоритмическом языке Matlab выдала вектор решения:
X ={5,1667, -10,1538,6,9005,-2,1667, 4,1538, -3,1795} кН
Листинг программы
% Решается система алгебраических уравнений АХ=b
Clearall;
tic
disp('начало______________________')
% Исходные данные:
a=1.6; h=2.6; l=3.6; F1=3; F2=6; q=2.8;
n=6; A=zeros(n,n); b=zeros(n,1); X=zeros(n,1);
% Элементыматрицы A
A(1,2)=1; A(1,5)=1; A(2,3)=-1; A(2,6)=1;
A(3,1)=1; A(3,4)=1; A(4,4)=a; A(4,6)=-h;
A(5,5)=h; A(6,5)=-a; A(6,6)=-l;
% Компонентывектораb
b(1)=-F2; b(2)=-q*l; b(3)=F1;
b(4)=F1*a; b(5)=F1*l; b(6)=F1*a;
% Решение системы уравнений: АХ=b
X=A\b
disp('конец_______________________')
toc
>>Zhukov
начало______________________
X =
5.1667
-10.1538
6.9005
-2.1667
4.1538
-3.1795
конец_______________________
Elapsed time is 0.000191 seconds.
Расчёт плоской фермы
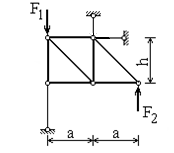
Плоская ферма состоит из семи стержней и держится на трёх опорных стержнях (рис. 1). Определить усилия в стержняхс помощью вычислительного комплекса МАТЛАБ.
Исходные данные
| Шифр | а м | h м | F1 кН | F2 кН |
| 19–4 | 2,9 | 3,1 | 7 | 5 |
| Исходная схема | Расчётная схема | |
| 
| |
| Рис. 1 | Рис. 2 |
Решение
Ферма и приложенные силы находится в вертикальной плоскости и представляют плоскую систему. Для неё соблюдается условие статической определённости в виде соотношения между количествами стержней, узлов и опорных стержней:
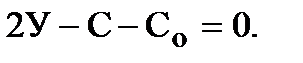
Количество узлов 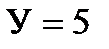 , стержней
, стержней 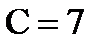 , опорных стержней Co=3. Очевидно, что условие выполняется.
, опорных стержней Co=3. Очевидно, что условие выполняется.
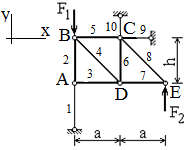
Изобразим расчётную схему (рис. 2). Покажем координатные оси х, у, отметим узлы A, B, C, D, E, B, номера стержней 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.
Приступим к определению усилий в стержнях методом вырезания узлов. С этой целью вырежем узлы A, B, C, D, E, B, (рис. 3), обозначим продольные силы в сечениях стержней 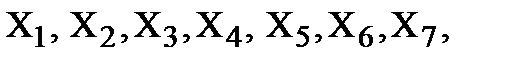
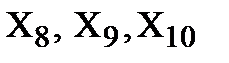 .
.
Необходимые для составления уравнений равновесия углы наклона стержней к к оси x - ов найдём по рис. 2,3:
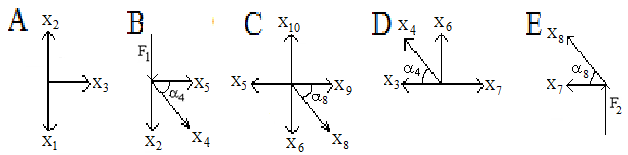
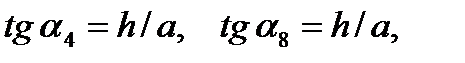
Тригонометрические функции, требующиеся далее при составлении уравнений равновесия, легко определяются по известным формулам их соотношений:

Рассмотрим условия равновесия каждого узла.
Узел A . Предполагая сходящиеся к нему стержни 1 и 2 растянутыми, изобразим узел и силы, приложенные к нему. Составим уравнения равновесия в виде равенства нулю сумм проекций сил на координатные оси x, y:
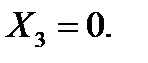 (1)
(1)
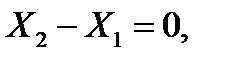 (2)
(2)
Аналогично составляем уравнения равновесия для других узлов:
Узел B .
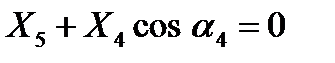 , (3)
, (3)
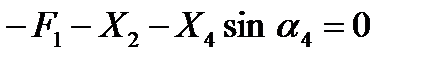 . (4)
. (4)
Узел C .
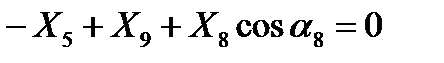 , (5)
, (5)
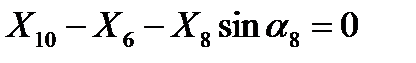 . (6)
. (6)
Узел D .
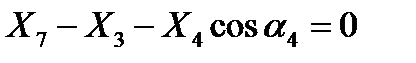 . (7)
. (7)
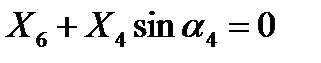 . (8)
. (8)
Узел E .
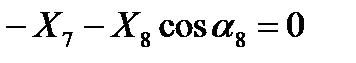 . (9)
. (9)
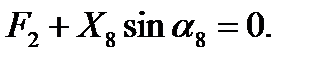 (10)
(10)
Коэффициенты при неизвестных и свободные члены вышеприведённых уравнений (1)- (10) образуют матрицу А и вектор b, cпомощью которых можно найти неизвестные опорные реакции и усилия в стержнях фермы из соответствующей системы алгебраических уравнений
AX = b, (11)
где А – квадратная матрица порядка n=10, b – десятимерный вектор. Выпишем их более наглядно.
A = 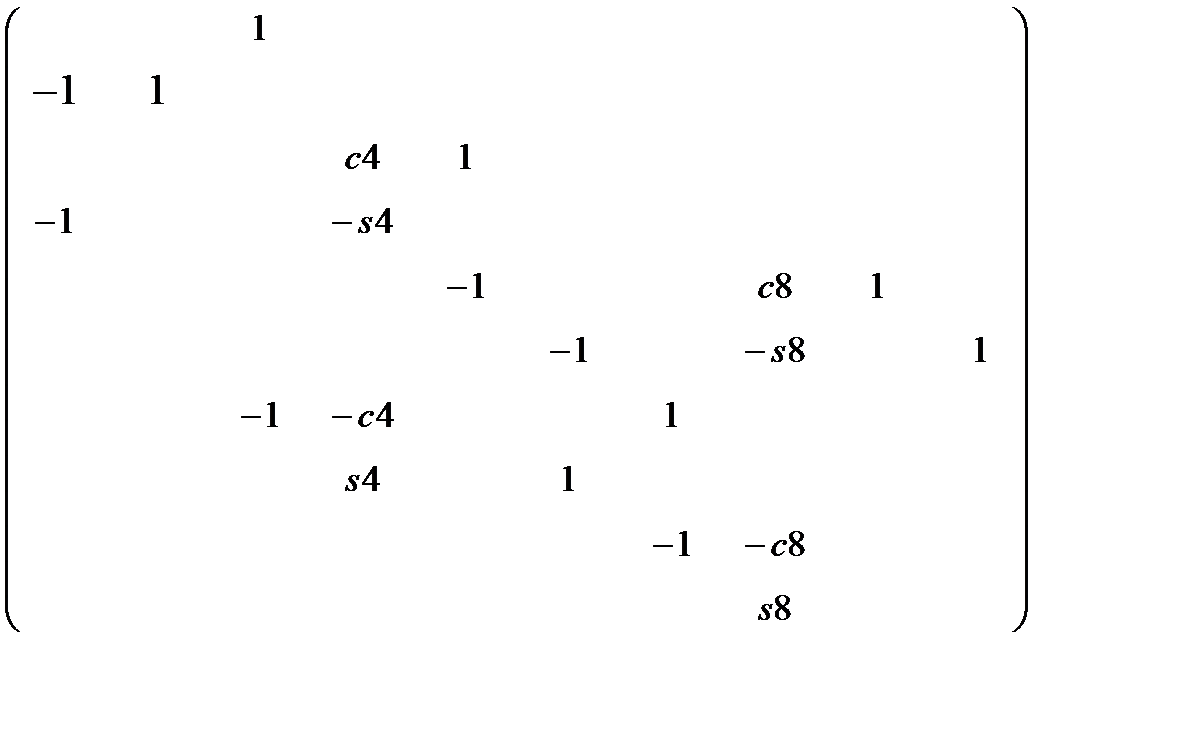 , b=
, b= 
Компьютерная программа на алгоритмическом языке Matlab выдала вектор решения:
X = {-12,0000 -12,0000 0 6,8468
-4,6774 5,0000 4,6774 -6,8468 0 -10,0000} кН.
Отрицательным значениям соответствуют сжатые стержни.
Листинг программы на алгоритмическом языке МАТЛАБ
% Жуков Т.А. Шифр 19-4 30.10.2018
% Расчёт плоской фермы
% Решается система алгебраических уравнений АХ=b
clearall;
tic
disp('начало______________________')
% Исходные данные:
a=2.9; h=3.1; F1=7; F2=5;
n=10; A=zeros(n,n); b=zeros(n,1); X=zeros(n,1);
tg4=h/a;
tg8=h/a;
c4=1/sqrt(1+tg4^2); s4=sqrt(1-c4^2);
c8=1/sqrt(1+tg8^2); s8=sqrt(1-c8^2);
% Элементы матрицы A и вектора b
A(1,3)=1 ; b(4)=F1;
A(2,1)=-1; A(2,2)=1;
A(3,4)=c4; A(3,5)=1;
A(4,2)=-1; A(4,4)=-s4; b(10)=-F2;
A(5,5)=-1; A(5,8)=c8; A(5,9)=1;
A(6,6)=-1; A(6,8)=-s8; A(6,10)=1;
A(7,3)=-1; A(7,4)=-c4; A(7,7)=1;
A(8,4)=s4; A(8,6)=1;
A(9,7)=-1; A(9,8)=-c8;
A(10,8)=s8;
% Решениесистемыуравнений: АХ=b
X=A\b
disp('конец_______________________')
toc
Дата: 2018-12-28, просмотров: 543.