Статическими массивами
Цель работы: закрепить практические навыки работы с системой программирования языка С++ на примере реализации алгоритмов над статическими массивами.
Основные теоретические сведения
Одномерные массивы
Массив представляет собой структуру данных, позволяющую хранить под одним именем совокупность данных любого, но только одного какого-то типа. Массив характеризуется своим именем, типом хранимых элементов и размерностью (количеством хранимых элементов).
Объявление переменной как одномерного массива имеет вид:
тип имя_массива [размерность]
В качестве размерности в объявлении массива разрешено использовать только константные выражения, ввиду чего такой массив будет являться статическим. Тип массива может быть любым.
Например,
int A [10];
объявляет массив с именем А, содержащий 10 целых чисел.
Доступ к элементам массива осуществляется выражением
имя_массива [номер_элемента]
где номер_элемента – индекс, являющийся целочисленным значением в диапазоне от 0 до размерность – 1. То есть номер первого элемента равен 0, а номер последнего элемента на 1 меньше размерности массива. Для предыдущего примера, А[0] - значение первого элемента, А[1] - второго, А[9] - последнего.
Работа с массивами, как правило, непосредственно связана с использованием операторов цикла.
Ниже приведен пример заполнения массива числами Фибоначчи, первые 2 из которых равны 1, а каждое последующее равно сумме двух предыдущих.
#include<iostream.h>
main()
{
int B[20];
B[0]=1;
B[1]=1;
for (int i=2; i<20; i++)
B[i]=B[i-1]+B[i-2];
for (i=0; i<20; i++)
cout <<"B["<<i<<"]="<<B[i]<<endl;
}
При объявлении массива значения элементов носят случайный характер, поэтому иногда желательно совместить объявление массива с заданием элементам начальных значений, т.е. инициализацией. Эти значения перечисляются в списке инициализации после знака равенства, разделяются запятыми и заключаются в фигурные скобки. Например:
int A[10] ={1,2,3,4,5,6,7,8,9,10};
double S[5] ={0.1,2.0,-3.2,0,6.5};
Таким образом, после данных объявлений A[2] будет содержать значение 3, а S[3] значение 0.
Если начальных значений меньше, чем элементов в массиве, оставшиеся элементы автоматически получают нулевые начальные значения. Например, оператор
int A[10] ={1,2,3};
задает значения первым трем элементам, а остальные будут равны 0. Оператор
int A[10] ={0};
присваивает нулевые значения всем элементам массива.
В объявлении массива со списком инициализации размерность массива можно не указывать. Тогда количество элементов массива будет равно количеству элементов в списке начальных значений. Например, объявление
double S[] ={0.1,2.0,-3.2,0,6.5};
создает массив из пяти элементов.
В объявлении массива в качестве размерности лучше всегда использовать именованные константы. Ниже приведен пример объявление массива, заполнение его случайными значениями от -10 до 10 и подсчет суммы его элементов:
#include<iostream.h>
#include<stdlib.h>
main()
{
randomize();
double c[15];
for (int i=0; i<15; i++)
c[i]=10-double(random(201))/10;
for (int i=0; i<15; i++)
cout <<"c["<<i<<"]="<<c[i]<<endl;
double S=0;
for (int i=0; i<15; i++) S+=c[i];
cout<<"S="<<S;
}
Если в дальнейшем потребуется массив не из 15 элементов, а, например, из 100, нужно будет изменить размерность массива и в объявлении, и во всех операторах, работающих с этим массивом (в данном случае в операторах for. Таких операторов в разных программах может быть очень много и поэтому она плохо масштабируется. Грамотнее будет реализовать этот пример следующим образом:
#include<iostream.h>
#include<stdlib.h>
main()
{
const int N=15; // объявление константы
randomize();
double c[N];
for (int i=0; i<N; i++)
c[i]=10-double(random(201))/10;
for (int i=0; i<N; i++)
cout <<"c["<<i<<"]="<<c[i]<<endl;
double S=0;
for (int i=0; i<N; i++) S+=c[i];
cout<<"S="<<S;
}
В этом случае мы вводим именованную константу N и используем ее во всех операторах, в которых требуется указать размерность массива. Тогда при необходимости изменения размерности массива, достаточно будет изменить его только в объявлении константы N.
const int N=100;
Программа сразу становится масштабируемой. А объявление N как константы гарантирует, что объявленное значение не будет случайно изменено где-то в программе.
Аналогичный результат можно получить, если заменить объявление константы директивой компилятора #define
#define N 10
В ряде случаев требуются константные массивы, данные из которых программа может только читать. Такие массивы обязательно должны инициализироваться в момент объявления. Например, требуется неизменяемый массив простых чисел, значения которых не больше 30:
const prime[] = {2,3,5,7,11,13,17,19,23,29};
Двумерные массивы
По аналогии с одномерными массивами, можно объявлять и многомерные статические массивы, т.е. массивы, элементами которых являются массивы. Например, двумерный массив можно объявить следующим образом:
int A2 [10] [3];
Такое объявление описывает двумерный массив, который можно представить себе как матрицу, состоящую из 10 строк и 3 столбцов.
Доступ к значениям элементов многомерного массива обеспечивается через номера элементов, заключенные в квадратные скобки. Например, А2[3][2] – значение элемента, лежащего на пересечении четвертой строки и третьего столбца. Также как и при работе с одномерными массивами номера элементов начинаются с 0.
Если многомерный массив инициализируется при его объявлении, список значений по каждой размерности заключается в фигурные скобки. Приведенный ниже оператор объявляет двумерный массив С размерностью 4 на 3 и инициализируется.
int C[4][3]= {{1,2,3},{4,5,6},{7,8,9},{10,11,12}};
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
| 10 | 11 | 12 |
В этом случае, элемент С[1][2] равен 6, а элемент С[2][1] равен 8 и т.д.
Если в списке инициализации в какой-то из размерностей не хватает данных, то все дальнейшие не перечисленные элементы считаются равными нулям. Например
double D [5] [4] = {{1.0,2.1,3.2,1.8},
{-4.1,5.0,1.1},
{-7.1,2.2}};
создаст матрицу размерностью 5 на 4, состоящую из элементов вещественных чисел и присвоит им следующие начальные значения:
| 1.0 | 2.1 | 3.2 | 1.8 |
| -4.1 | 5.0 | 1.1 | 0 |
| -7.1 | 2.2 | 0 | 0 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 |
Работа с двумерными массивами непосредственно связана с использованием одновременно двух операторов цикла, внешнего и внутреннего. Например, необходимо определить в двумерном случайно заполненном массиве, каких чисел больше положительных или отрицательных. Ноль во внимание не принимается:
#include<iostream.h>
#include<stdlib.h>
main()
{
const int n=5;
const int m=10;
randomize();
int matr[n][m];
int i,j;
for (i=0; i<n; i++)
for (j=0; j<m; i++) matr[i][j]=100-random(201);
for (i=0; i<n; i++) {
for (j=0; j<m; i++) cout <<matr[i][j]<<" ";
cout <<endl;
}
int p=0;
for (i=0; i<n; i++)
for (j=0; j<m; i++)
if (matr[i][j]!=0)
if (matr[i][j]>0) p++;
else p--;
if (p==0) cout <<"равное количество";
else if (p>0) cout <<"положительных больше";
else cout <<"отрицательных больше";
}
Сортировка массивов
Задачей сортировки массивов является преобразование исходной последовательности элементов массива в последовательность, содержащую те же элементы, но в порядке возрастания (или убывания) значений.
Сортировка методом выбора. При сортировке массива a[0], a[1], ..., a[N-1] методом простого выбора среди всех элементов находят элемент с наибольшим значением a[i], и этот элемент ставят в самый конец массива, т.е. поменять местами значения элементов массива a[ i ] и a[ N -1]. Далее, игнорируя последний элемент массива a[ N-1], следует выполнить поиск наибольшего элемента в подмассиве a[0], a[1], ..., a[ N -2] и поменять его местами с последним элементом подмассива a[ N -2]. Этот процесс повторяется до тех пор, пока не будут найдены N -1 наибольших значений и не дойдем до подмассива a[0], содержащего к этому моменту наименьшее значение. Работа алгоритма иллюстрируется следующим примером:
| Исходная последовательность N =7: | ||||||
| 3 | 1 | 7 | 5 | 6 | 4 | 2 |
| max =7 из a[0]…a[N-1] | ||||||
| 3 | 1 | 2 | 5 | 6 | 4 | 7 |
| max =6 из a[0]…a[N-2] | ||||||
| 3 | 1 | 2 | 5 | 4 | 6 | 7 |
| max =5 из a[0]…a[N-3] | ||||||
| 3 | 1 | 2 | 4 | 5 | 6 | 7 |
| max =4 из a[0]…a[N-4] | ||||||
| 3 | 1 | 2 | 4 | 5 | 6 | 7 |
| max =3 из a[0]…a[N-5] | ||||||
| 2 | 1 | 3 | 4 | 5 | 6 | 7 |
| max =2 из a[0]…a[1] | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Программная реализация этого метода на языке Си++, будет выглядеть следующей:
#include<iostream.h>
#include<stdlib.h>
main()
{
const N=7; //размерность массива
int A[N];
randomize();
int i;
for(i=0; i<N; i++) A[i]=random(10);//заполнение массива
int index, max,j;
for (i=N-1; i>0; i--)
{ max=A[0];
index=0;
for(j=1; j<=i; j++)
if (A[j]>max) { index=j;
max=A[j];
}
A[index]=A[i];
A[i]=max;
}
}
Если в условии if(A [ j ]> max), поменять знак операции сравнения на меньше (<), то будут выбираться наименьшие значения и сортировка массива будет осуществляться по убыванию.
Сортировка методом обмена. При сортировке массива a[0], a[1], ..., a[ N -1] методом обмена (“методом пузырька”), начиная с первого элемента сравнивают два соседних элемента (a[ i ] и a[ i +1]) и меняют их местами, если a[ i ]>a[ i +1], т.е. если они нарушают порядок. Такое сравнение и обмен выполняют до тех пор, пока не будет достигнут конец массива и последним элементом a [ N -1] окажется элемент массива с наибольшим значением. Далее, игнорируя последний элемент массива a[ N -1], следует повторить такую же схему сравнения и обмена в подмассиве a[0], a[1], ..., a[ N -2]. И так далее. На последнем шаге будут сравниваться только текущие значения a[0] и a[1]. Работа алгоритма иллюстрируется следующим примером:
| Исходная последовательность N =5: | 6 | 3 | 7 | 1 | 5 |
| Шаг 1: | 6 | 3 | 7 | 1 | 5 |
| 3 | 6 | 7 | 1 | 5 | |
| 3 | 6 | 7 | 1 | 5 | |
| 3 | 6 | 1 | 7 | 5 | |
| 3 | 6 | 1 | 5 | 7 | |
| Шаг 2: | 3 | 6 | 1 | 5 | 7 |
| 3 | 6 | 1 | 5 | 7 | |
| 3 | 1 | 6 | 5 | 7 | |
| 3 | 1 | 5 | 6 | 7 | |
| Шаг 3: | 3 | 1 | 5 | 6 | 7 |
| 1 | 3 | 5 | 6 | 7 | |
| 1 | 3 | 5 | 6 | 7 | |
| Шаг 4: | 1 | 3 | 5 | 6 | 7 |
| 1 | 3 | 5 | 6 | 7 | |
| Итоговая последовательность: | 1 | 3 | 5 | 6 | 7 |
Программная реализация этого метода на языке Си, будет выглядеть следующей:
#include<iostream.h>
#include<stdlib.h>
main()
{
const N=7;
int A[N];
randomize();
int i;
for (i=0; i<N; i++) A[i]=random(100);
int swap, j;
for (i=N-1; i>1; i--)
for(j=0; j<i; j++)
if (A[j]>A[j+1]) {swap=A[j+1];
A[j+1]=A[j];
A[j]=swap;
}
}
Если в условии if (A[j]>A[j+1]), поменять знак операции сравнения на меньше (<), то последними элементами в подмассивах будут оказываться наименьшие значения и сортировка массива будет осуществляться по убыванию.
Сортировка челночным методом. При сортировке массива a[0], a[1], ..., a[ N -1] челночным методом, начиная с первого элемента сравнивают два соседних элемента (a[ i ] и a[ i +1]), если порядок нарушен (a[ i ]<=a[ i +1]), то продвигаются на один элемент вперед (i = i +1), если порядок нарушен (a[ i ]>a[ i +1]), то производится перестановка и сдвигаются на один элемент назад ( i = i -1). Таким образом сравнивая и переставляя элементы доходят до конца массива ( i = N -1), при этом массив становится упорядоченным. Работа алгоритма иллюстрируется следующим примером:
| Исходная последовательность N =5 | 3 | 1 | 7 | 5 | 2 |
| i=0 (порядок нарушен) | 3 | 1 | 7 | 5 | 2 |
| i=0 (порядок не нарушен) | 1 | 3 | 7 | 5 | 2 |
| i=1 (порядок не нарушен) | 1 | 3 | 7 | 5 | 2 |
| i=2 (порядок нарушен) | 1 | 3 | 7 | 5 | 2 |
| i=1 (порядок не нарушен) | 1 | 3 | 5 | 7 | 2 |
| i=2 (порядок не нарушен) | 1 | 3 | 5 | 7 | 2 |
| i=3 (порядок нарушен) | 1 | 3 | 5 | 7 | 2 |
| i=2 (порядок нарушен) | 1 | 3 | 5 | 2 | 7 |
| i=1 (порядок нарушен) | 1 | 3 | 2 | 5 | 7 |
| i=0 (порядок не нарушен) | 1 | 2 | 3 | 5 | 7 |
| i=1 (порядок не нарушен) | 1 | 2 | 3 | 5 | 7 |
| i=2 (порядок не нарушен) | 1 | 2 | 3 | 5 | 7 |
| i=3 (порядок не нарушен) | 1 | 2 | 3 | 5 | 7 |
| i=4: Итоговая последовательность | 1 | 2 | 3 | 5 | 7 |
Программная реализация этого метода на языке Си++, будет выглядеть следующей:
#include<iostream.h>
#include<stdlib.h>
main()
{
const N=7;
int A[N];
randomize();
int i;
for (i=0; i<N; i++) A[i]=random(100);
int swap;
i=0;
while (i<N-1)
if (A[i]>A[i+1]) {swap=A[i+1];
A[i+1]=A[i];
A[i]=swap;
i--;
if (i<0) i=0;
}
else i++;
}
Если в условии if (A[ i ]>A[ i +1]), поменять знак операции сравнения на меньше (<), то сортировка массива будет осуществляться по убыванию.
Сортировка методом вставок. Данный метод сортировки массива основан на вставке элементов из неупорядоченной части массива в упорядоченную. Считается, что первоначально массив a[0], a[1], ..., a[ N -1] является не отсортированным, поэтому упорядоченная часть будет состоять из одного первого элемента a[0], а неупорядоченная из всех элементов массива a[1], ..., a[ N -1]. На каждом шаге метода из неупорядоченной части извлекается первый элемент и помещается в упорядоченную, так чтобы не нарушался порядок. При этом количество элементов в упорядоченной части увеличивается на 1, а в неупорядоченной уменьшается на 1. Процесс вставки элементов происходит до тех пор, пока весь массив не окажется отсортированным.
| Исходная последовательность N =7: | 3 | 1 | 7 | 5 | 6 | 4 | 2 | |
| 3 | 1 | 7 | 5 | 6 | 4 | 2 | ||
| 1 | 3 | 7 | 5 | 6 | 4 | 2 | ||
| 1 | 3 | 7 | 5 | 6 | 4 | 2 | ||
| 1 | 3 | 5 | 7 | 6 | 4 | 2 | ||
| 1 | 3 | 5 | 6 | 7 | 4 | 2 | ||
| 1 | 3 | 4 | 5 | 6 | 7 | 2 | ||
| Итоговая последовательность: | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
Программная реализация этого метода на языке Си, будет выглядеть следующей:
#include<iostream.h>
#include<stdlib.h>
main()
{
const N=7;
int A[N];
randomize();
int i,j,element;
for (i=0; i<N; i++) A[i]=random(100);
for (i=1; i<N; i++)
{ element=A[i];
j=i;
while (A[j-1]>element)
{A[j]=A[j-1];
j--;
if (j<1) break;
}
A[j]=element;
}
for (i=0; i<N; i++) cout << A[i]<< " ";
}
Если в условии while (A [ j -1]> element), поменять знак операции сравнения на меньше (<), то сортировка массива будет осуществляться по убыванию.
Примеры программ, реализующие алгоритмы работы со статическими массивами
Пример 1. Среди заданных N точек на плоскости найти две, что прямые, проходящие через них перпендикулярно соединяющему эти точки отрезку, образуют полосу, в которой содержится максимальное количество точек из множества N.
Рассмотрим для решения этой задачи необходимые сведения и формулы.
Уравнение прямой, проходящей через точки P, Q, имеет вид:
,
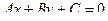где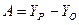 
, 
,
;
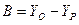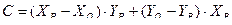Уравнение прямой, проходящей через точку P перпендикулярно отрезку PQ, имеет вид:
,
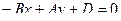где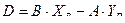 
.
Если в уравнении прямой подставить координаты точек, лежащих по одну сторону от этой прямой, получим значения одного знака, иначе – разных знаков.
#include<iostream.h>
#include<stdlib.h>
#include<conio.h>
main()
{
clrscr();
const int N=20;
randomize();
double x[N];
double y[N];
int i;
for (i=0; i<N; i++)
{
x[i]=double(random(401)-200)/10;
y[i]=double(random(401)-200)/10;
}
for (i=0; i<N; i++)
cout <<i+1<<"-точка ("<<x[i]
<<";"<<y[i]<<");"<<endl;
double A,B,C;
double AP,BP,CP;
double AQ,BQ,CQ;
double Z1,Z2,Z3;
int max=0,tek,P,Q,N1,N2;
//выбираем очередную пару точек
for(P=0; P<N-1; P++)
for(Q=P+1; Q<N; Q++)
{
//находим коэффициенты уравнения прямой PQ
A=y[P]-y[Q];
B=x[Q]-x[P];
C=(x[P]-x[Q])*y[P]+(y[Q]-y[P])*x[P];
//прямые, проходящие через P, Q перпендикулярно PQ
AP=-B;
BP=A;
CP=B*x[P]-A*y[P];
AQ=-B;
BQ=A;
CQ=B*x[Q]-A*y[Q];
//определим, сколько точек попадает в полосу
tek=0;
Z1=AP*x[Q]+BP*y[Q]+CP;
Z3=AQ*x[P]+BQ*y[P]+CQ;
//просматриваем все точки, кроме P и Q
for(i=0; i<N; i++)
if (i!=Q && i!=P)
{
//точки i и Q должны быть по одну сторону от
//прямой, проходящей через P
Z2=AP*x[i]+BP*y[i]+CP;
if (Z1*Z2>0)
{
//точки i и P должны быть по одну сторону от
//прямой, проходящей через Q
Z2=AQ*x[i]+BQ*y[i]+CQ;
if (Z3*Z2>0) tek++;
}
}
if (tek>max)
{
max=tek;
N1=P;
N2=Q;
}
}
cout<<"Исходные точки:"<<endl
<<"("<<x[N1]<<";"<<y[N1]<<")"<<endl
<<"("<<x[N2]<<";"<<y[N2]<<")"<<endl;
getch();
}
Пример 2. Дано множество A из N пар точек с целочисленными координатами. Расположить точки данного множества по возрастанию значений пересечения прямой, проходящей через эту точку, с осью абсцисс. Пары точек, через которые проходит прямые параллельные прямые исключить из сортировки. Сортировку произвести методом обмена.
#include<iostream.h>
#include<conio.h>
#include<stdlib.h>
main()
{
const N=10;
int X1[N],Y1[N];
int X2[N],Y2[N];
int i;
randomize();
//заполнение массивов случайным образом
for (i=0;i<N;i++)
{
X1[i]=random(41)-20;
Y1[i]=random(41)-20;
X2[i]=random(41)-20;
Y2[i]=random(41)-20;
}
//вывод первоначальных данных
for (i=0;i<N;i++)
cout<<i+1<<" пара точек:"<<endl
<<"("<<X1[i]<<";"<<Y1[i]<<") "
<<"("<<X2[i]<<";"<<Y2[i]<<") "<<endl;
int R=N;
i=0;
int swapX1,swapX2,swapY1,swapY2;
//исключение пар точек, прямые через которые
//параллельны оси абсцисс, поместив их в конец
//массива
while (i<R && R>1)
if (Y1[i]==Y2[i]) {
swapX1=X1[R-1];
swapY1=Y1[R-1];
swapX2=X2[R-1];
swapY2=Y2[R-1];
X1[R-1]=X1[i];
Y1[R-1]=Y1[i];
X2[R-1]=X2[i];
Y2[R-1]=Y2[i];
X1[i]=swapX1;
Y1[i]=swapY1;
X2[i]=swapX2;
Y2[i]=swapY2;
R--;
}
else i++;
//сортировка R пар точек, прямые через которые
//пересекаю ось абсцисс
int j;
double A1,A2;
for (i=R-1; i>1; i--)
for(j=0; j<i; j++)
{
A1=(X1[j]-X2[j])*Y1[j]-(Y1[j]-Y2[j])*X1[j];
A1=A1/(Y1[j]-Y2[j]);
A2=(X1[j+1]-X2[j+1])*Y1[j+1]-(Y1[j+1]-
Y2[j+1])*X1[j+1];
A2=A2/(Y1[j+1]-Y2[j+1]);
if (A1>A2) { swapX1=X1[j+1];
swapY1=Y1[j+1];
swapX2=X2[j+1];
swapY2=Y2[j+1];
X1[j+1]=X1[j];
Y1[j+1]=Y1[j];
X2[j+1]=X2[j];
Y2[j+1]=Y2[j];
X1[j]=swapX1;
Y1[j]=swapY1;
X2[j]=swapX2;
Y2[j]=swapY2;
}
}
//Вывод исключенных пар точек
if (R!=N)
{
cout<<"Исключенные точки:"<<endl;
for (i=R;i<N;i++)
cout <<"("<<X1[i]<<";"<<Y1[i]<<") "
<<"("<<X2[i]<<";"<<Y2[i]<<") "<<endl;
}
//Вывод отсортированных пар точек
cout<<"Отсортированные пары точек:"<<endl;
for (i=0;i<R;i++)
cout <<"("<<X1[i]<<";"<<Y1[i]<<") "
<<"("<<X2[i]<<";"<<Y2[i]<<") "<<endl;
getch();
}
Варианты заданий
ЗАДАНИЕ I:
Для всех вариантов заполнение массива организовать в ходе выполнения программы вводом значений с клавиатуры. Также в вариантах, где задан упорядоченный по возрастанию массив, осуществить проверку правильности ввода значений.
1. Дан массив, заполненный целочисленными значениями. Найти количество его локальных минимумов и максимумов, а также определить из них максимальный и минимальный.
2. Дан массив, заполненный целочисленными значениями. Определить количество его промежутков монотонности (то есть участков, на которых его элементы возрастают или убывают).
3. Дан целочисленный массив размера N. Если он является перестановкой, то есть содержит все числа от 1 до N, то вывести 0, в противном случае вывести номер первого недопустимого элемента.
4. Дан целочисленный массив. Назовем серией группу подряд идущих одинаковых элементов, а длиной серии — количество этих элементов (длина серии может быть равна 1). Вывести массив, содержащий длины всех серий исходного массива.
5. Дано множество A из N точек с координатами ( x , y ). Среди всех точек этого множества найти точки наиболее близкие и наиболее удаленные от начала координат, лежащие в первой, второй, третьей и четвертой четверти.
6. Дано множество A из N точек с координатами ( x , y ). Найти пары различных точек этого множества с минимальным и максимальным расстоянием между ними и сами эти расстояния.
7. Дано множество A из N точек с координатами ( x , y ). Найти две точки из данного множества. Для одной точки сумма расстояний до остальных точек должна быть минимальна, а для другой максимальна.
8. Даны множества A и B, состоящие соответственно из N1 и N2 точек с координатами ( x , y ). Найти минимальное и максимальное расстояние между точками этих множеств и сами точки, расположенные на этом расстоянии.
9. Дано множество A из N точек с координатами ( x , y ). Найти наименьший периметр треугольника, вершины которого принадлежат различным точкам множества A, и сами эти точки (точки выводятся в том же порядке, в котором они перечислены при задании множества A).
10. Дано множество A из N точек с координатами ( x , y ). Найти три точки из этого множества, которые составляли бы вершины треугольника, и сумма расстояний от сторон до других точек была бы минимальна.
11. Дано множество A из N точек с координатами ( x , y ). Определить количество прямоугольных треугольников, которые создаются этими точками.
12. Дано множество A из N точек с координатами ( x , y ). Найти точку из этого множества, которая являлась бы центром окружности с минимальным радиусом. Все точки множества должны находится внутри этой окружности.
13. Дано множество A из N точек с координатами ( x , y ). Найти наибольшую длину ломанной линии, которую можно составить из точек этого множества.
14. Секретный замок для сейфа состоит из 10 расположенных в ряд ячеек, в которые надо вставить игральные кубики. Но дверь открывается только в том случае, когда в любых трех соседних ячейках сумма точек на передних гранях кубиков равна 10. (Игральный кубик имеет на каждой грани от 1 до 6 точек.) Напишите программу, которая разгадывает код замка при условии, что два кубика уже вставлены в ячейки.
15. В целочисленном массиве найти повторяющиеся числа. Вывести эти числа, а также количество их повторений.
16. Дано вещественное число x и целочисленный массив. В массиве найти два члена, расположенных в диапазоне между максимальным и минимальным значениями, среднее арифметическое которых ближе всего к x.
17. Даны две последовательности: a 1 , a 2 , ..., an и b 1 , b 2 , ..., bm (m < n). В каждой из них члены различны. Определить входят ли все члены второй последовательности в первую последовательность, а также вывести те значения первой последовательности, которые не представлены во второй.
18. Задан массив A размером N. Определить значения k (k ≠0 и k ≠ N -1), при котором выполняется соотношение:
|max(A[0]...A[k])-max(A[k+1]...A[N-1])|< |min(A[0]...A[k])-min(A[k+1]...A[N-1])|.
19. Дан массив целых чисел М1. Вводим массив М2, размер которого значительно меньше, чем у М2. Определить, сколько раз массив М2 встречается в М1.
20. Проверить, существует ли в заданном целочисленном массиве такой диапазон чисел, которые являются элементами арифметической или геометрической прогрессии. При существовании вывести первые и последние элементы этого диапазона.
21. Написать программу определения в одномерном массиве целых чисел наибольшего количества последовательно расположенных чисел, образующих «пилу». Например, пилу
образуют числа 3, 7, 5, 9, 2, 4, 1, 6.
22. Задан упорядоченный по возрастанию массив целых чисел. Написать программу, позволяющую вставить в этот массив вводимое с клавиатуры число без нарушения упорядоченности. Предполагается, что размер заданного массива не увеличивается. Поэтому требуется определить, вставлять ли в массив элемент, по величине больший (меньший) всех элементов массива. Это можно сделать, удалив наименьший (наибольший) по величине элемент. Затем нужно определиться с направлением сдвига элементов при освобождении места. Если исключить вариант вставки таких элементов и сдвигать в сторону большие по величине элементы, то останется только определить место вставки, сдвинуть элементы, освобождая место для вставки, и вставить вводимое число.
23. Образуем числовую последовательность. Начальный элемент — произвольное натуральное число, кратное трем; за любым элементом последовательности следует число, равное сумме кубов всех цифр данного элемента. Доказать, что такая последовательность, начиная с некоторого места, становится постоянной и равной некоторому числу. Чему равно это число? Примечание: Числовую последовательность реализовать в виде массива.
24. Первый член последовательности — четырехзначное целое число, цифры которого не все одинаковые. Каждый последующий элемент образуется следующим образом. Цифры предыдущего элемента располагаем в убывающем порядке (первое число) и в возрастающем порядке (второе число). Из первого числа вычитаем второе и получаем следующий элемент последовательности. Показать, что такая последовательность, начиная с некоторого элемента, становится постоянной и равной некоторому числу. Чему равно это число? Примечание: Числовую последовательность реализовать в виде массива.
25. В одномерном массиве с четным количеством элементов (2N) находятся координаты N точек плоскости. Они располагаются в следующем порядке: х1, у1, х2, у2, х3, у3 и т. д.
Определить номера точек, которые могут являться вершинами равнобедренного треугольника.
26. Задан целочисленный массив размерности N. Определить, есть ли среди элементов массива простые числа. Если да, то вывести номера этих элементов.
27. На плоскости n точек заданы своими координатами, а также дана окружность радиуса R с центром в начале координат. Указать множество всех треугольников с вершинами в заданных точках, пересекающихся с окружностью.
28. В одномерном массиве все отрицательные элементы переместить в начало массива, а остальные – в конец с сохранением порядка следования. Дополнительный массив заводить не разрешается.
29. В одномерном массиве с четным количеством элементов (2 N) находятся координаты N точек плоскости. Они располагаются в следующем порядке: х1, у1, х2, у2, х3, у3 и т. д. Определить номера точек, которые могут являться вершинами квадрата.
30. В одномерном массиве с четным количеством элементов (2 N) находятся координаты N точек плоскости. Они располагаются в следующем порядке: х1, у1, х2, у2, х3, у3 и т. д. Определить три точки, являющиеся вершинами треугольника, для которого разность точек вне его и внутри является минимальной.
31. Дано множество A из N точек с координатами ( x , y ). Найти такие пары точек этого множества, что проведенные через них линии параллельны осям координат.
32. Задан массив A размером N. Определить значения k (k ≠0 и k ≠ N -1), при котором соотношение |max ( A [0]... A [ k ])- max ( A [ k +1]... A [ N -1])| является минимальным.
33. Разделить массив на две части, поместив в первую элементы, большие среднего арифметического их суммы, а во вторую меньшие (сортировку не использовать)
34. Дан массив из N четырехзначных натуральных чисел. Определить и вывести на экран все группы чисел, у которых суммы первых двух цифр и суммы двух последних цифр равны.
35. Дано множество C комплексных чисел, состоящее из двух массивов вещественных чисел A и B размерностью N (c=a+jb). Найти минимальное и максимальное значения аргумента комплексного числа в диапазоне между максимальным и минимальным значениями модуля комплексного числа. Примечание: модуль комплексного числа определяется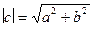 
, а аргумент 
.
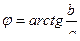36. Дан массив неповторяющихся целых чисел. Найти наименьшее число элементов, которые нужно выкинуть из данной последовательности, чтобы осталась возрастающая последовательность.
37. На координатной плоскости дано множество парабол, которые описываются уравнениями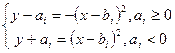 
. Параметры парабол ai и bi заключены в вещественных массивах A и B размерностью N. Определить пары парабол, которые не пересекаются.
38. На координатной плоскости дано N точек с координатами ( x , y ). Найти такие пары точек этого множества, что проведенные через них прямые линии пересекают одновременно и окружность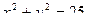 
и квадратичную параболу 
.
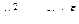39. На координатной плоскости дано N точек с координатами ( x , y ), которые являются вершинами N – угольника. Найти площадь и периметр заданного N – угольника, а также определить является ли он правильным.
40. Дан массив из N натуральных целых чисел. Найти наименьшее общее кратное этих чисел.
41. Дан массив из N натуральных целых чисел. Определить последовательность простых чисел, которые встречаются среди множителей значений заданного массива хотя бы один раз. Примечание: Использовать дополнительный массив для хранения последовательности простых чисел не разрешается. (Пример: { 2, 6, 14, 37, 22}-> 2, 3, 7, 11, 37).
42. Дан массив из N натуральных целых чисел. Определить пару чисел, которые имеют наибольшее количество одинаковых делителей.
43. Дано множество A из N точек с координатами ( x , y ). Найти точку с минимальным суммарным отклонением от других точек заданного множества.
44. Дан массив из N натуральных целых чисел. Определить пары троек чисел с равными суммами. Примечание: Одно и тоже число не может входить одновременно в обе тройки.
45. Задан целочисленный массив A размером N. Определить при каком значении индекса k (k ≠0 и k ≠ N -1), заданный массив разбивается на две числовые последовательности с наиболее близкими средними арифметическими значениями.
46. Даны две последовательности вещественных чисел X и Y размерностью N 1 и N 2. Определить при каких значениях 
и 
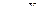функция 
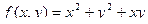примет минимальное и максимальное значения.
47. Даны две последовательности целых чисел X и Y размерностью N 1 и N 2. Определить такие значения i и j, при которых выражение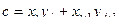 
является наибольшей.
48. Даны два целочисленных массива разной размерностью. Считать, что среднее арифметическое значение первого массива больше, чем среднее арифметическое второго. За минимальное количество обменов элементами между массивами, преобразовать их так, чтобы среднее арифметическое первого массива стало меньше второго.
49. Дана целочисленная последовательность A размерностью N. Найти наименьшее число K элементов, которые можно выкинуть из данной последовательности, так чтобы осталась возрастающая последовательность.
50. Даны две последовательности целых чисел X и Y размерностью N. Определить такие значения i и j, при которых выражение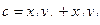 
является наименьшей.
ЗАДАНИЕ II:
Для всех вариантов заполнение массива организовать с помощью датчика случайных чисел.
1 – 4. Дано множество С, состоящее из массивов вещественных чисел A и B размерностью N. Причем значения элементов массива B определяются следующим образом: B [0]=0, B [ i ]= A [ i ]- A [ i -1] i =1.. N -1. Считать, что значение множества С[ k ]≥ C [ m ], если либо A [ k ]≥ A [ m ] или A [ k ]< A [ m ] и A [ k ]+ B [ k ]≥ A [ m ]+B [ m ]. Отсортировать множество С по возрастанию в соответствии с указанным условием. Сортировку произвести:
1. методом обмена;
2. методом вставкой;
3. методом выбора;
4. методом Шелла.
5 – 8. Дано множество C комплексных чисел, состоящее из двух массивов вещественных чисел A и B размерностью N (c=a+jb). Отсортировать данное множество комплексных чисел по убыванию значений их модулей. Примечание: модуль комплексного числа равен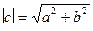 
. Сортировку произвести:
5. методом обмена;
6. методом вставкой;
7. методом выбора;
8. методом Шелла.
9 – 12. Целочисленный массив X из n элементов разбит на m фрагментов. В целочисленном массиве K из m элементов хранятся длины соответствующих фрагментов (все K [ i ] различны, их сумма равна n). Упорядочить массив K по возрастанию, переставив соотвествующие фрагменты в массиве X.
Сортировку произвести:
9. методом обмена;
10. методом вставкой;
11. методом выбора;
12. методом Шелла.
13 – 16. Дана некоторая функция f ( x , y ) и множество A из N точек с целочисленными координатами ( x , y ), состоящее из двух массивов. Известно, что значение функции f ( x , y ) в точке ( x 0 , y 0 ) равно площади фигуры, образованной прямыми y = x 0 и x = y 0 c осями координат. Расположить точки данного множества в соответствии с убыванием значений заданной функции.
Сортировку произвести:
13. методом обмена;
14. методом вставкой;
15. методом выбора;
16. методом Шелла.
17 – 20. Дано множество A из N точек с координатами ( x , y , z ). Расположить точки данного множества по увеличению расстояния от начала координат до соответствующей точки.
Сортировку произвести:
17. методом обмена;
18. методом вставкой;
19. методом выбора;
20. методом Шелла.
21 – 24. Дан целочисленный массив A из N точек. Расположить значения данного массива по убыванию в диапазоне между максимальным и минимальным значениями. Максимальное и минимальное значение не входят в диапазон сортировки.
Сортировку произвести:
21. методом обмена;
22. методом вставкой;
23. методом выбора;
24. челночным методом.
25 – 28. Дана некоторая функция f ( x , y ) и множество A из N точек с целочисленными координатами ( x , y ), состоящее из двух массивов. Известно, что значение функции f ( x , y ) в точке ( x 0 , y 0 ) равно площади фигуры, образованной осями координат и прямой, проходящей через точку ( x 0 , y 0 ) под углом 45 ° к осям в той четверти координат, где находится эта точка. Расположить точки данного множества в соответствии с увеличением значений заданной функции.
Сортировку произвести:
25. методом обмена;
26. методом вставкой;
27. методом выбора;
28. челночным методом.
29 – 32. Даны два целочисленных массива A и B из N точек. Отсортировать массив A по возрастанию, а массив B по убыванию и после этого поменять местами четные элементы массивов. Затем отсортировать массив A по убыванию, а массив B по возрастанию.
Сортировку массивов произвести:
29. методом обмена;
30. методом вставкой;
31. методом выбора;
32. челночным методом.
33 – 36. Дана некоторая функция f ( x , y ) и множество A из N точек с целочисленными координатами ( x , y ), состоящее из двух массивов. Известно, что значение функции f ( x , y ) в точке ( x 0 , y 0 ) равно площади фигуры, образованной осью абсцисс и прямой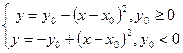 
. Расположить точки данного множества в соответствии с убыванием значений заданной функции.
Сортировку произвести:
33. методом обмена;
34. методом вставкой;
35. методом выбора;
36. челночным методом.
37 – 40. Даны два массива A и B вещественных чисел по N элементов. Считая, что массивы представляют единую последовательность из (2N) чисел, отсортировать массивы по возрастанию. Примечание: использовать дополнительный массив для слияния заданных массивов нельзя.
Сортировку массивов произвести:
37. методом обмена;
38. методом вставкой;
39. методом выбора;
40. челночным методом.
41 – 44. В результате эксперимента получено n пар значений величин x и y в массивах X ( n ) и Y ( n ). Массив X не упорядочен, но не содержит одинаковых элементов. Получить значения функции y ( x ) с постоянным шагом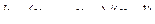 
, где 
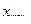и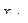 
- соотвественно наибольшее и наименьшее значения в массиве X . Значения y с постоянным шагом вычислить по формуле линейной интерполяции соседних наблюдений (после упорядочения по x):
.
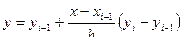Сортировку массива X произвести:
41. методом обмена;
42. методом вставкой;
43. методом выбора;
44. челночным методом.
45 – 48. В результате эксперимента получены наборы значений аргумента x и соответствующих значений функции y. Сформировать третий массив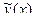 
по возрастанию значений аргумента из значений функции 
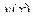. Если одному значению x соответствует несколько значений y, взять их среднее значение.
Сортировку массива аргумента осуществить:
45. методом обмена;
46. методом вставкой;
47. методом выбора;
48. челночным методом.
49 – 50. В неупорядоченном массиве из N элементов есть совпадающие значения. Вначале упорядочить массив по убыванию, а затем из каждой группы одинаковых элементов оставить только один, удалив остальные и поджав массив к его началу.
Сортировку массива осуществить:
49. методом вставкой;
50. челночным методом.
Лабораторная работа №5
Дата: 2019-02-02, просмотров: 381.
