Если функция 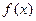 непрерывна на отрезке
непрерывна на отрезке 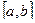 и известна ее первообразная функция
и известна ее первообразная функция 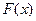 , то определенный интеграл этой функции в пределах от a до b может быть вычислен по формуле Ньютона – Лейбница
, то определенный интеграл этой функции в пределах от a до b может быть вычислен по формуле Ньютона – Лейбница
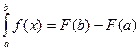 .
.
Однако во многих случаях первообразная функция 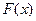 не может быть найдена или является слишком сложной. Вследствие этого вычисления определенного интеграла по формуле Ньютона – Лейбница может быть затруднительным или практически невозможным. Кроме того, на практике подынтегральная функция
не может быть найдена или является слишком сложной. Вследствие этого вычисления определенного интеграла по формуле Ньютона – Лейбница может быть затруднительным или практически невозможным. Кроме того, на практике подынтегральная функция 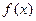 часто задается таблично и тогда само понятие первообразной теряет смысл. Поэтому, важное значение имеют приближенные и, в первую очередь, численные методы вычисления определенных интегралов.
часто задается таблично и тогда само понятие первообразной теряет смысл. Поэтому, важное значение имеют приближенные и, в первую очередь, численные методы вычисления определенных интегралов.
Численные методы позволяют избежать громоздких расчетов в тех случаях, когда результат приемлем с определенной степенью точности. Точность вычислений 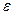 (максимально допустимая ошибка в результате всех вычислений, из которых складывается погрешность), как правило, оговаривается заранее при постановке задачи. Точность вычислений будет достигнута, если абсолютная погрешность (абсолютное значение разности между точным и приближенным значениями) не превосходит
(максимально допустимая ошибка в результате всех вычислений, из которых складывается погрешность), как правило, оговаривается заранее при постановке задачи. Точность вычислений будет достигнута, если абсолютная погрешность (абсолютное значение разности между точным и приближенным значениями) не превосходит 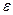 (очень маленькое положительное число).
(очень маленькое положительное число).
Сущность большинства численных методов вычисления определенных интегралов состоит в замене подынтегральной функции 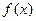 аппроксимирующей функцией
аппроксимирующей функцией 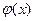 , для которой легко можно отыскать первообразную среди элементарных функций:
, для которой легко можно отыскать первообразную среди элементарных функций:
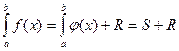 ,
,
где S - приближенное значение интеграла,
R - погрешность вычисления интеграла.
Следует отметить тот факт, что погрешность уменьшается при увеличении числа n точек разбиения отрезка 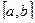 за счет более точной аппроксимации подынтегральной функции, однако при этом будет возрастать погрешность суммирования частичных интегралов, и, начиная с некоторого значения n 0 она станет достаточно большой. Поэтому возникает необходимость разработки оценки погрешности каждого из методов интегрирования.
за счет более точной аппроксимации подынтегральной функции, однако при этом будет возрастать погрешность суммирования частичных интегралов, и, начиная с некоторого значения n 0 она станет достаточно большой. Поэтому возникает необходимость разработки оценки погрешности каждого из методов интегрирования.
Формулы приближенного интегрирования (квадратурные формулы) можно найти в справочниках по высшей математике. Приведем основные формулы численного интегрирования для методов левых прямоугольников, трапеций и Симпсона.
Метод левых прямоугольников. Пусть I - точное значение интеграла 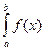 ,
, 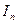 - приближенное значение интеграла, полученное при разбиении отрезка интегрирования на n равных частей,
- приближенное значение интеграла, полученное при разбиении отрезка интегрирования на n равных частей, 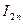 - приближенное значение интеграла при удвоенном числе точек разбиения,
- приближенное значение интеграла при удвоенном числе точек разбиения, 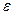 - заданная точность вычислений. Тогда для метода левых прямоугольников квадратурная формула будет иметь вид
- заданная точность вычислений. Тогда для метода левых прямоугольников квадратурная формула будет иметь вид
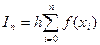 ,
,
где 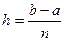 ,
, 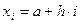 .
.
Оценка точности вычислений:
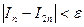 .
.
Следовательно, как только выполнится условие 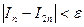 , это будет означать, что
, это будет означать, что 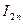 является приближенным значением для I с точностью
является приближенным значением для I с точностью 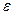 .
.
Метод трапеций. Для метода трапеций квадратурная формула будет иметь вид
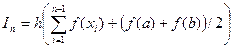 ,
,
где 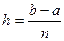 ,
, 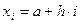 .
.
Оценка точности вычислений:
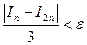 .
.
Следовательно, как только выполнится условие 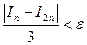 , это будет означать, что
, это будет означать, что 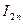 является приближенным значением для I с точностью
является приближенным значением для I с точностью 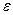 .
.
Метод Симпсона. Для метода Симпсона квадратурная формула будет иметь вид
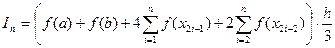 ,
,
где 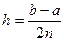 ,
, 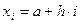 .
.
Оценка точности вычислений:
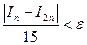 .
.
Следовательно, как только выполнится условие 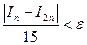 , это будет означать, что
, это будет означать, что 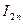 является приближенным значением для I с точностью
является приближенным значением для I с точностью 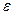 .
.
При программной реализации методов численного интегрирования, как правило, задаются оценкой точности вычислений 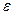 и первоначальным количеством отрезков интегрирования n. Определяют приближенные значения интегралов по квадратурным формулам для n и 2 n отрезков и вычисляют оценку точности по формулам, исходя из конкретного метода интегрирования. Если вычисленная точность меньше заданной, то считается, что значение интеграла, полученное для 2 n отрезков, является приближенным значением с точностью
и первоначальным количеством отрезков интегрирования n. Определяют приближенные значения интегралов по квадратурным формулам для n и 2 n отрезков и вычисляют оценку точности по формулам, исходя из конкретного метода интегрирования. Если вычисленная точность меньше заданной, то считается, что значение интеграла, полученное для 2 n отрезков, является приближенным значением с точностью 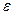 . Если вычисленная точность больше заданной, то увеличивают количество отрезков интегрирования n в два раза и повторяют процедуру вычислений до тех пор, пока вычисленная точность будет меньше заданной.
. Если вычисленная точность больше заданной, то увеличивают количество отрезков интегрирования n в два раза и повторяют процедуру вычислений до тех пор, пока вычисленная точность будет меньше заданной.
Примеры, реализующие алгоритмы разветвляющейся структуры
Пример 1. Дана числовая последовательность и некоторое число e. Найти наименьший номер члена последовательности, для которого выполняется условие 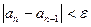 . Вывести на экран этот номер и все элементы
. Вывести на экран этот номер и все элементы 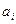 , где i =1,2,…, n.
, где i =1,2,…, n. 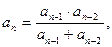
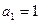 ,
, 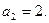 (при организации циклического повторения, следует использовать оператор цикла с постусловием do … while).
(при организации циклического повторения, следует использовать оператор цикла с постусловием do … while).
#include<iostream.h>
#include<math.h>
main()
{
double e;
cout <<"Введите e=";
cin >>e;
double a_n;
double a_n_1=2;
double a_n_2=1;
cout <<"a1="<<a_n_2<<endl;
cout <<"a2="<<a_n_1<<endl;
int i=2;
do { a_n=(a_n_1-a_n_2)/(a_n_1*a_n_2);
if(fabs(a_n-a_n_1)<e) { cout <<"a"<<i++<<"="<<a_n<<endl;
a_n_2=a_n_1;
a_n_1=a_n;
}
else break;l
} while (1);
cout<<"Последний номер последовательности"<<i;
}
Пример 2. Вычислить значения определенного интеграла 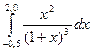 методом Симпсона с заданной точностью
методом Симпсона с заданной точностью 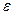 . (при организации циклического повторения, следует использовать оператор цикла с предусловием while).
. (при организации циклического повторения, следует использовать оператор цикла с предусловием while).
#include<iostream.h>
#include<math.h>
main()
{
const double a=-0.5;
const double b=2;
double e;
cout <<"Введите заданную точность=";
cin >>e;
int n;
cout <<"Введите начальное количество отрезков интегрирования=";
cin >>n;
double In=0,I2n=0;
double h,x;
int i;
while (!In||!I2n||fabs(I2n-In)/15>e)
{In=I2n;
h=(b-a)/(2*n);
I2n=a*a/((1+a)*(1+a)*(1+a));
I2n+=b*b/((1+b)*(1+b)*(1+b));
i=1;
while(i<=n) { x=a+h*(2*i-1);
I2n+=4*x*x/((1+x)*(1+x)*(1+x));
i++;
}
i=2;
while(i<=n) { x=a+h*(2*i-2);
I2n+=2*x*x/((1+x)*(1+x)*(1+x));
i++;
}
I2n=I2n*h/3;
n=n*2;
}
cout <<"Значение интеграла="<<I2n;
}
Пример 3. Дано натуральное число N. Выдать все пары “близнецов”, меньших N. “Близнецами” называют простые числа, разность между которыми равна 2. (при организации циклического повторения, следует использовать оператор цикла for):
#include<iostream.h>
main()
{
int N;
cout <<"Введите N=";
cin >>N;
int j,k;
for (int i=2; i<N-2; i++)
{for (j=2;i%j;j++);
for (k=2;(i+2)%k;k++);
if((j==i)&&(k==i+2))cout<<"("<<i<<";"<<i+2<<")-близнецы"
<< endl;
}
}
Варианты заданий
ЗАДАНИЕ I (для всех вариантов задания, при организации циклического повторения, следует использовать оператор цикла с постусловием do … while):
1 – 14. Дан числовой ряд и некоторое число e. Найти сумму тех членов ряда (n =1,2,3…), модуль которых больше или равен заданному числу e и вывести на экран все элементы числового ряда, которые входят в сумму. Общий член ряда имеет вид:
1. 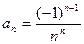 ;
2. ;
2. 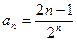 ;
3. ;
3. 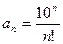 ;
4. ;
4. 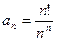 ;
5. ;
5. 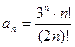 ;
6. ;
6. 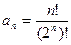 ;
7. ;
7. 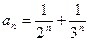 ; ;
| 8. 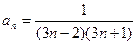 ;
9. ;
9. 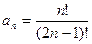 ;
10. ;
10. 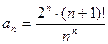 ;
11. ;
11. 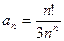 ;
12. ;
12. 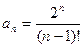 ;
13. ;
13. 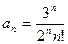 ;
14. ;
14. 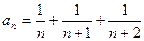 ; ;
|
15 – 28. Дана числовая последовательность и некоторое число e. Найти наименьший номер члена последовательности, для которого выполняется условие 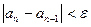 . Вывести на экран этот номер и все элементы
. Вывести на экран этот номер и все элементы 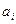 , где i =1,2,…, n.
, где i =1,2,…, n.
15. 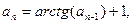 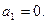 16.
16. 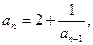 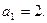 17.
17.  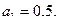 18.
18. 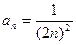 .
19. .
19. 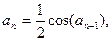 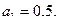 20.
20. 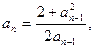 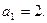 21.
21. 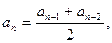
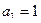 , , 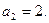
| 22. 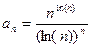 .
23. .
23. 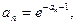 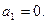 24.
24. 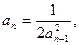 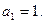 25.
25. 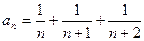 .
26. .
26. 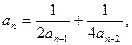
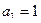 , , 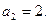 27.
27. 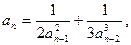
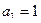 , , 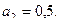 28.
28. 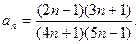
|
29 – 32. Дана числовая последовательность и некоторое число e. Найти наименьший номер элемента последовательности, для которого выполняется условие M. Вывести на экран номер и все элементы 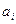 , где i =1,2,…, n.
, где i =1,2,…, n.
29. 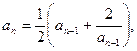 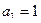 , ,
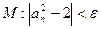 .
30. .
30. 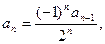 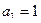 , ,
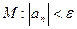 . .
| 31. 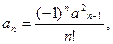 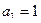 , ,
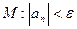 .
32. .
32. 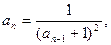 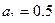 , ,
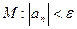 .
33. .
33. 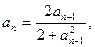 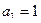 , ,
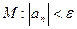
|
34 – 41. Составить программу для вычисления значений функции F ( x ) на отрезке [a , b] с шагом h. Результат представить в виде таблицы, первый столбец которой – значения аргумента, второй – соответствующие значения функции.
34. 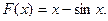 35.
35. 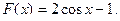 36.
36. 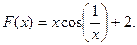 37.
37. 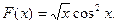
| 38. 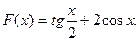 39.
39. 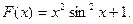 40.
40. 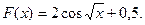 41.
41. 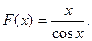
|
42 – 46. Дано натуральное число N . Вычислить
42. 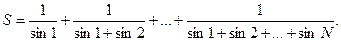
43. 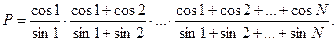
44. 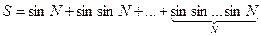 .
.
45. 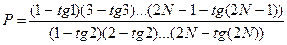 .
.
46 – 50. Даны натуральные числа n и k. Вычислить
46. 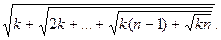
47. 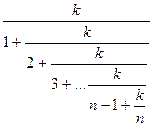 .
.
48. 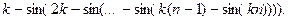
49. 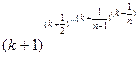 .
.
50. 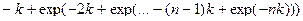 .
.
ЗАДАНИЕ II :
Вычислить значения определенных интегралов 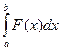 методом прямоугольников, методом трапеций и методом Симпсона с заданной точностью
методом прямоугольников, методом трапеций и методом Симпсона с заданной точностью 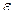 . Вычисления организовать в одном цикле таким образом, что при достижении требуемой точности вычисления интеграла одним методом, продолжать вычисления интеграла другими методами. (Для всех вариантов задания, при организации циклического повторения, следует использовать оператор цикла с предусловием while):
. Вычисления организовать в одном цикле таким образом, что при достижении требуемой точности вычисления интеграла одним методом, продолжать вычисления интеграла другими методами. (Для всех вариантов задания, при организации циклического повторения, следует использовать оператор цикла с предусловием while):
1. 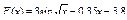 .
2. .
2. 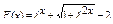 .
3. .
3. 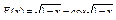 .
4. .
4. 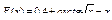 .
5. .
5. 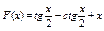 .
6. .
6. 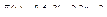 .
7. .
7. 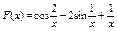 .
8. .
8. 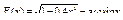 .
9. .
9. 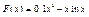 .
10. .
10. 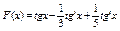 .
11. .
11. 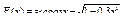 .
12. .
12. 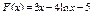 .
13. .
13. 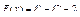 .
14. .
14. 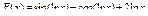 .
15. .
15.  .
16. .
16. 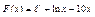 .
17. .
17. 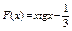 .
18. .
18. 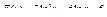 .
19. .
19. 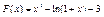 .
20. .
20. 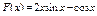 .
21. .
21. 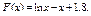 22.
22. 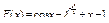 .
23. .
23. 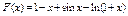 .
24. .
24. 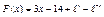 .
25. .
25.  . .
| 26. 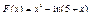 .
27. .
27. 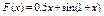 .
28. .
28. 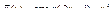 .
29. .
29. 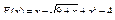 .
30. .
30. 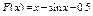 .
31. .
31. 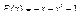 .
32. .
32. 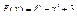 .
33. .
33. 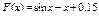 .
34. .
34. 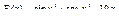 .
35. .
35. 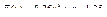 .
36. .
36. 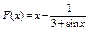 37.
37. 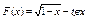 .
38. .
38. 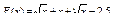 .
39. .
39. 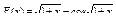 .
40. .
40. 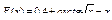 .
41. .
41. 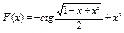 .
42. .
42. 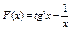 .
43. .
43. 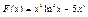 .
44. .
44. 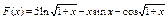 .
45. .
45. 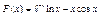 .
46. .
46. 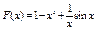 .
47. .
47. 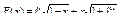 .
48. .
48. 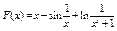 .
49. .
49. 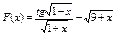 .
50. .
50. 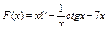 . .
|
ЗАДАНИЕ III (для всех вариантов задания, при организации циклического повторения, следует использовать оператор цикла for):
1. Определить существует ли двузначное число, которое равно квадрату числа его единиц, сложенному с кубом числа его десятков.
2. Определить, существует ли такая четверка последовательных натуральных чисел, сумма квадратов которых равна сумме квадратов трех следующих натуральных чисел.
3. Определить, является ли заданное число совершенным, т.е. равным сумме всех своих (положительных) делителей, кроме самого этого числа (например, число 6 совершенно: 6=1+2+3).
4. Найти все двузначные числа, удвоенная сумма цифр которых равна их произведению? (Пример: 36, 44, 63).
5. Найти все двузначные числа, равные утроенному произведению своих цифр. (Пример: 15, 24).
6. Найти все двузначные числа, которые обладают следующим свойством: куб суммы цифр числа равен квадрату самого числа. (Пример: 27).
7. Найти все трехзначные числа, представимые в виде сумм факториалов своих цифр. (Пример: 145).
8. Найти все трехзначные числа, которые можно представить разностью между квадратом числа, образованного первыми двумя цифрами и квадратом третьей цифры. (Пример: 100).
9. Найти все двузначные числа, сумма цифр которых не меняется при умножении числа на 2,3,4,5,6,7,8,9.
10. Можно ли заданное натуральное число М представить в виде суммы квадратов двух натуральных чисел? Написать программу решения этой задачи.
11. Привести дробь вида 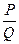 к несократимому виду.
к несократимому виду.
12. Дано натуральное число N. Найти и вывести все числа в интервале от 1 до N -1, у которых сумма всех цифр совпадает с суммой цифр данного числа. (Пример: N=44 – 17, 26, 35).
13. Дано натуральное число N. Найти наибольшее число M (M>1), на которое сумма цифр в цифровой записи числа N делится без остатка. (Пример: N=12345, сумма=15, M=5).
14. Найти все целые корни уравнения 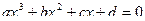 , где a , b , c и d – заданные целые числа, причем
, где a , b , c и d – заданные целые числа, причем 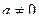 и
и 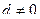 . Примечание: целыми корнями могут быть только положительные и отрицательные делители коэффициента d.
. Примечание: целыми корнями могут быть только положительные и отрицательные делители коэффициента d.
15. Натуральные числа a , b , c называются числами Пифагора, если выполняется условие 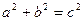 . Напечатать все числа Пифагора меньше заданного.
. Напечатать все числа Пифагора меньше заданного.
16. Долгожитель (возраст менее 100 лет) обнаружил однажды, что если к сумме квадратов цифр его возраста прибавить число дня его рождения, то как раз получится его возраст. Сколько лет долгожителю.
17. Найти наименьшее натуральное число n, представимое двумя различными способами в виде суммы кубов двух натуральных чисел.
18. Найти все натуральные числа, не превосходящие n, квадрат суммы цифр которых равен самому числу.
19. Найти все n – значные числа, сумма квадратов цифр которых кратна M.
20. Найти все натуральные числа, не превосходящие n, которые делятся на каждую из своих цифр без остатка.
21. Проверить, существует ли четырехзначное натуральное число, сумма пятых степеней цифр которого равна самому числу.
22. Проверить, существует ли четырёхзначное целое число, равное четвертой степени суммы своих цифр.
23. Определить пары натуральных чисел а < 100 и b < 100, произведение которых в 10 раз больше их суммы. Сколько таких пар?
24. Найдите все двузначные натуральные числа, которые равны утроенной сумме своих цифр.
25. Найдите все трехзначные натуральные числа, равные сумме кубов своих цифр.
26. Христиан Гольдбах, выдвинул так называемую проблему Гольдбаха, которая предполагает, что всякое целое число, большее или равное 6, может быть представлено в виде суммы трех простых чисел. Проверьте утверждение Гольдбаха для чисел, не превышающих число 100.
27. Христиан Гольдбах выдвинул гипотезу о том, что любое четное число, большее 2, представимо в виде суммы двух простых чисел. Проверьте эту гипотезу Гольдбаха для вcex четных чисел, не превышающих число 100.
28. Определить количество делителей у каждого из натуральных чисел от 1 до n.
29. Найти натуральное трехзначное число, у которого количество делителей максимально. Если таких чисел несколько, то должно быть выбрано максимальное из них. Вывести это число, а также все делители этого числа.
30. Найти все трехзначные простые числа (простым называется натуральное число, большее 1 и не имеющее других делителей, кроме единицы и самого себя).
31. Найти все целые числа из промежутка от 300 до 600, у которых сумма делителей кратна 10.
32. Три натуральных числа образуют дружественную тройку, если сумма собственных делителей каждого числа равна сумме двух других чисел. Отыскать дружественные тройки натуральных чисел.
33. Два натуральных числа называются "дружественными", если каждое из них равно сумме всех делителей другого, за исключением его самого (таковы, например, числа 220 и 284). Напечатать все пары "дружественных" чисел, не превосходящих заданного натурального числа.
34. Решить задачу Ферма. Найти куб, который в сумме со всеми его собственными делителями дает квадрат.
35. Составить программу нахождения цифрового корня натурального числа. Цифровой корень числа получается следующим образом. Складываем все цифры этого числа, затем все цифры найденной суммы и т. д., пока в результате не будет получено однозначное число (цифра), которое и называется цифровым корнем данного числа.
36. Найти все простые несократимые дроби, заключенные между 0 и 1, знаменатели которых не превышают 7 (дробь задается двумя натуральными числами — числителем и знаменателем).
37. Проверить, действительно ли при четном n число 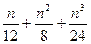 - целое.
- целое.
38. Составить программу, которая находит наибольшее значение отношения трехзначного числа к сумме его цифр.
39. Найти натуральное двухзначное число, у которого количество простых делителей максимально. Если таких чисел несколько, то должно быть выбрано минимальное из них. Вывести это число, а также все простые делители этого числа.
40. Найти натуральные числа, не превосходящие заданного, у которых делители являются только простыми числами. Вывести эти числа, а также их делители.
41. Дано натуральное число n. Получить все натуральные числа, меньшие n и взаимно простые с ним (два натуральных числа называются взаимно простыми, если их наибольший общий делитель равен 1).
42. Натуральное число из n цифр называется числом Армстронга, если сумма его цифр, возведенная в степень n, равна самому числу. Подсчитать все числа Армстронга из двух и трех цифр.
43. Найти двухзначное число а b, чтобы выполнялось уравнение 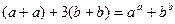 .
.
44. Определите количество наборов четырех различных нечетных натуральных чисел, сумма которых равна числу 50. Вывести наборы этих чисел.
45. Найти все трехзначные числа abc, у которых делителем является наименьшее общее кратное чисел a, b, c.
46. Найти все четырехзначные числа abc d, у которых делителем является наибольший общий делитель двухзначных чисел ab и c d .
47. Найти двухзначные числа, которые раскладываются на неповторяющиеся простые множители.
48. Дано натуральное число N. Найти и вывести все числа в интервале от 1 до N -1, у которых произведение всех цифр совпадает с суммой цифр данного числа. (Пример: N=44 – 18, 24).
49. Дано натуральное число N. Среди чисел 1... N такие, запись которых совпадает с последними цифрами записи их квадратов. (Пример: 62=36, 252=25).
50. Найти двухзначные числа, которые при возведении в квадрат дают палиндромы. Палиндром – это сочетание символов, которые читаются одинаково в прямом и обратном направлениях. (Пример: 262=676).
Лабораторная работа №4
Дата: 2019-02-02, просмотров: 537.