Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Функция	Прототип и краткое описание действий
abs	int abs(int i); Возвращает абсолютное значение целого аргумента i.
acos	double acos(double x); Функция арккосинуса. Значение аргумента должно находится в диапазоне от -1 до +1.
asin	double asin(double x); Функция арксинуса. Значение аргумента должно находится в диапазоне от -1 до +1.
atan	double atan(double x); Функция арктангенса.
atan2	double atan2(double y, double x); Функция арктангенса от значения y/x.
cosh	double cosh(double x); Возвращает значение гиперболического косинуса x
exp	double exp(double x); Вычисляет значение ех (экспоненциальная функция).
fabs	double fabs(double x); Возвращает абсолютное значение вещественного аргумента x двойной точности.

Продолжение табл.7

Функция	Прототип и краткое описание действий
floor	double floor(double x); Находит наибольшее целое, не превышающее значения х. Возвращает его в форме double.
fmod	double fmod(double x, double y); Возвращает остаток от деления нацело x на y.
log	double log(double x); Вычисляет значение натурального логарифма ln x.
log10	double log10(double x); Вычисляет значение десятичного логарифма lg x.
labs	long labs(long x); Возвращает абсолютное значение целого аргумента long x.
ldexp	double ldexp(double v, int e); Возвращает значение выражения v*2e.
poly	double poly(double x, int n, double c[ ]); Вычисляет значение полинома: c[n]xn + c[n-1]xn-1 + . . . +c[1]x + c[0].
pow	double pow(double x, double y); Возвращает значение x в степени y (xy).
pow10	double pow10(int p); Возвращает значение 10p.
sin	double sin(double x); Функция синуса. Угол (аргумент) задается в радианах.
sinh	double sinh(double x); Возвращает значение гиперболического синуса для x.
sqrt	double sqrt(double x); Возвращает положительное значение квадратного корня Öx
tan	double tan(double x); Функция тангенса. Угол (аргумент) задается в радианах.
tanh	double tanh(double x); Возвращает значение гиперболического тангенса x.

 

Пример программы, реализующей алгоритм линейной структуры

Заданы вершины треугольника А(x1,y1), B(x2,y2), C(x3,y3). Вычислить длину медианы, проведенной из А.

 

//Подключение средств консольного потокового

// ввода / вывода

#include<iostream.h>

//Подключение математических функций

#include<math.h>

//Подключение библиотеки для использования функции

//getch()

#include<conio.h>

//главная функция

main()

{

//Объявление переменных для задания координат

// точек треугольника

double Ax,Ay,Bx,By,Cx,Cy;

//Ввод координат точки А

cout<<"Введите координаты точки А:"<<endl;

cout<<"x=";

cin>>Ax;

cout<<"y=";

cin>>Ay;

//Ввод координат точки B

cout<<"Введите координаты точки B:"<<endl;

cout<<"x=";

cin>>Bx;

cout<<"y=";

cin>>By;

//Ввод координат точки C

cout<<"Введите координаты точки C:"<<endl;

cout<<"x=";

cin>>Cx;

cout<<"y=";

cin>>Cy;

//Объявление переменных, в которых будут

//находится длины сторон

double ab,bc,ca;

//Вычисление стороны AB

ab=sqrt((Ax-Bx)*(Ax-Bx)+(Ay-By)*(Ay-By));

//Вычисление стороны BC

bc=sqrt((Bx-Cx)*(Bx-Cx)+(By-Cy)*(By-Cy));

//Вычисление стороны CA

ca=sqrt((Cx-Ax)*(Cx-Ax)+(Cy-Ay)*(Cy-Ay));

//Объявление переменной для медианы

// и вычисление ее через длины

//сторон треугольника

double M=sqrt(2*ab*ab+2*ca*ca-bc*bc)/2;

//Вывод значения длины медианы

cout<<"Длина медианы, из точки А равна:”

<<M<<endl;

cout<<"Для завершения нажмите любую клавишу";

getch();

}

Примечание: Чтобы сразу после окончания работы программы окно, в ко­тором программа работала, не было автоматически перекрыто другим окном, например окном редактора текста среды раз­работки, в конце програм­мы желательно использовать функцию getch(), которая приостанавливает выполнение программы до тех пор, пока не будет нажата любая клавиша.

Варианты заданий

1. Заданы координаты трех вершин треугольника (х₁, у₁), (х₂, у₂),(x₃, y₃). Найти его периметр и площадь.

2. Длина отрезка задана в дюймах (1 дюйм = 2,54 см). Перевести значение длины в метрическую систему, то есть выразить ее в метрах, сантиметрах и миллиметрах. Например: 21 дюйм = 0 м 53 см 3.4 мм.

3. В такси одновременно сели три пассажи­ра. Когда вышел первый пассажир, на счетчике было p ₁ рублей; когда вышел второй p ₂ рублей. Сколько дол­жен был заплатить каждый пассажир, если по оконча­нии поездки счетчик показал p ₃ рублей? Плата за посад­ку составляет p ₀ рублей.

4. Дана сторона равностороннего треугольника. Найти радиусы и площади вписанной и описанной окружностей.

5. Коммерсант, имея стартовый капитал k рублей, занялся торговлей, которая ежемесячно увеличивает капитал на р%. Через сколько лет, он накопит сумму s, достаточную для покупки собственного магазина?

6. Треугольник задан величинами своих углов и радиусом опи­санной окружности. Найти стороны треугольника.

7. Селекционер вывел новый сорт зерновой культуры и снял с опытной делянки k кг семян. Посеяв 1 кг семян, можно за сезон собрать р кг семян. Через сколько лет селекционер сможет засеять новой культурой поле площадью s га, если норма высева n кг/га?

8. Найти площадь равнобедренной трапеции с основаниями а и b и углом a при большем основании а.

9. Треугольник задается координатами своих вершин на плоскости: A (x₁, y₁), B(x₂, у₂), С(х₃, у₃). Найти длину и основание высоты, опущенной из вершины А на сторону ВС.

10. За первый год производительность труда на предприятии возросла на p₁ %, за второй и третий — соответственно на р2 и р3 %. Найти среднегодовой прирост производительности (в процентах).

11. Найти сумму членов арифметической прогрессии, если известны ее первый член, знаменатель и число членов прогрессии.

12. Заданы координаты точки подвески математического маятника А( x , y , z ) и координаты одной из точек его наивысшего подъема B(x₁, y₁, z₁). Найти координаты самой низкой точки траектории и другой наивысшей точки подъема.

13. Найти (в радианах и в градусах) все углы треугольника со сторонами а, b, с.

14. Русские неметрические единицы длины: 1 верста = 500 саженей; 1 сажень = 3 аршина; 1 аршин = 16 вершков; 1 вершок = 44,45 мм. Длина некоторого отрезка составляет р метров. Перевести ее в русскую неметрическую систему.

15. Составить программу перевода радианной меры угла в гра­дусы, минуты и секунды.

16. Вычислить высоты треугольника со сторонами а, b, с.

17. У квадрата ABCD на плоскости известны координаты двух противоположных вершин — точек А и С. Найти координаты точек В и D. Примечание: расположение квадрата произвольно, его стороны не обязательно параллельны координатным осям.

18. Вычислить медианы треугольника со сторонами а, b, с.

19. Автомобиль потребляет l литров топлива. Владелец автомобиля приобрел новый карбюратор, который экономит n % топлива, новую систему зажигания, которая экономит m % топлива, и поршневые кольца, экономящие k % топлива. Найти фактическую экономию топлива в процентах и количество потребляемого топлива.

20. Вычислить биссектрисы треугольника со сторонами а, b, с.

21. Треугольник задается координатами своих вершин на плоскости: A(x₁, y₁), B(x₂, у₂), С(х₃, у₃). Найти точку пересечения биссектрис треугольника ABC (центр вписанной в него окружности).

22. Дано натуральное число Т, которое представляет длитель­ность прошедшего времени в секундах. Вывести данное значение длительности в часах, минутах и секундах в следующей форме: НН ч ММ мин SS с.

23. Заданы два вектора с координатами (x ₁, y ₁, z ₁) и (x ₂, y ₂, z ₂). Определить угол между векторами.

24. Вычислить площадь и периметр правильного N-угольника, описанного около окружности радиуса R (рассмотреть N — цело­го типа, R — вещественного типа).

25. Задан вектор с координатами (х, у, z). Найти углы наклона этого вектора к координатным осям.

26. Найти площадь круга, вписанного в треугольник с задан­ными сторонами.

27. Треугольник задается координатами своих вершин на плоскости: A (x₁, y₁), B(x₂, у₂), С(х₃, у₃). Найти внутренние углы треугольника ABC (в градусах).

28. Найти площадь круга, описанного около треугольника с задан­ными сторонами.

29. Треугольник задан величинами своих углов и радиусом впи­санной окружности. Найти стороны треугольника.

30. Вычислить площадь и периметр правильного N-угольника, вписанного в окружность радиуса R (рассмотреть N — цело­го типа, R — вещественного типа).

31. Найти объем пирамиды, построенной на векторах А, В, С, как на сторонах. Вектора заданы координатами (х, у, z).

 

32.  Определить токи на резисторах R1..R7 электрической схемы.

 

 

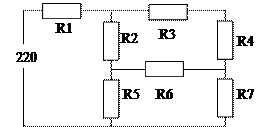32. Определить напряжение на резисторах R1..R7 электрической схемы.

 

 

34.  Определить число месяцев, через которое начальная сумма вклада в банке увеличится в три раза. Программа запрашивает ввод начальной суммы и ежемесячную процентную ставку.

35.  Треугольник задается координатами своих вершин на плоскости: A (x₁, y₁), B(x₂, у₂), С(х₃, у₃). Найти точку D, симметричную точке А относительно стороны ВС.

36.  Определить сумму денежного вклада через несколько месяцев при ежемесячной процентной ставке. Программа запрашивает ввод начальной суммы, ежемесячной процентной ставки и срока вклада.

37.  Заданы координаты трех вершин треугольника (х₁, у₁, z ₁), (х₂, у₂, z ₂),(x₃, y₃, z ₃). Найти его периметр и площадь.

 

38.  Определить координаты трех точек A, B, C пересечения фигур – двух окружностей с центрами (2,1) и (-5,0) и радиусами, равными 5, и прямой (с углом наклона a.).

 

 

39.  Определить координаты четырех точек пересечения A, B, C , D прямой y = kx +1 с окружностью (радиус равен 5) и квадратичной параболы y ² =- x +5.

 

 

 

40 - 45. Дан прямоугольный треугольник ABC (g = 90°), для которо­го определен следующий набор характерных параметров (рис.3 ): а, b , с — стороны треугольника; a , b — острые углы (в градусах); h — высота, опущенная на гипотенузу с; S — площадь; Р — пери­метр треугольника. По двум заданным параметрам вычислить все остальные. Сочетания данных параметров: 40. a, b; 41. a, c; 42. a, h; 43. b, a; 44. h, b; 45. c, b.		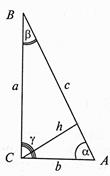Рис. 3
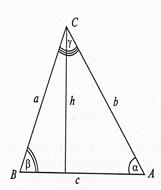
46.– 50. Дан произвольный треугольник ABC (рис. 4), для которого определен следующий набор характерных параметров: а, b, с - стороны треугольника; a , b , g — углы (в градусах); h — высота, опущенная на сторону с; S — площадь; Р — периметр треуголь­ника. По трем заданным параметрам вычислить все остальные. Сочетания данных параметров: 46. a , b , g ; 47. c , a , b ; 48. h , c , a ; 49. S , h , b ; 50. S , c , a ;

Рис. 4

     

Лабораторная работа №2