Аналогично одномерным массивам, можно с помощью указателя и операции new выделить место под двумерный динамический массив. Для этого используются массивы указателей, объявление которых имеет следующий вид:
тип_массива ** имя_указателя;
Данная запись может быть интерпретирована как объявление указателя на объект типа тип_массива *.
Выделение участка памяти указателю на объект типа тип_массива * с помощью операции new позволяет получить массив нужного размера, элементами которого являются также указатели, только на объекты типа тип_массива.
Например
double **B;
B=new double* [20];
выделяет место под массив указателей из 20 элементов.
Так как, каждый элемент массива указателей тоже является указателем, то ему соответственно также можно выделить некоторый участок памяти в виде массива, только уже вещественного типа
B[3]=new double [10];
Доступ к элементам созданного массива осуществляется через индекс элемента массива указателей и индекс массива, на который указывает элемент – указатель, а именно
B[3][5]=10;
Данная запись обращения к элементам аналогична доступу к элементам в двумерном статическом массиве.
Приведенный ниже пример создает двумерный динамический массив из n – строк и m – столбцов, введенных пользователем
int n,m;
double **matr;
cout << “n=”;
cin>>n;
cout << “m=”;
cin>>m;
//выделение места под массив указателей из
//n элементов, т.е. выделение места под n строк
matr=new double*[n];
//выделение места каждому указателю из массива //указателей по m вещественных элементов,
//т.е. выделение места под m столбцов
for (int i=0; i<n; i++)
matr[i]=new double[m];
Количество элементов, выделяемых всем указателям из массива указателей, не обязательно должно быть одинаковым. Пример
int n;
double **matr;
cout << “n=”;
cin>>n;
matr=new double*[n];
for (int i=0; i<n; i++)
matr[i]=new double[i+1];
реализует двумерный динамический массив в виде “лесенки со ступеньками”, т.е. первый указатель matr[0] будет содержать массив только из одного элемента, указатель matr[1] будет содержать массив из двух элементов, а последний указатель matr[n-1] будет содержать n элементов.
Освобождение памяти, выделенное под двумерный динамический массив, осуществляется в обратном порядке по отношению к выделению памяти, т.е. вначале освобождается память, выделенная под каждый элемент – указатель, а затем освобождается память, выделенная под массив указателей. Следующая запись демонстрирует освобождение памяти, выделенное в предыдущем примере
for (int i=0; i<n; i++)
delete [] matr[i];
delete []matr;
Примеры программ, реализующие алгоритмы работы с динамическими массивами
Пример 1. Даны три одномерных массива А, B , C, состоящие из N вещественных значений. Сформировать массив K такой же длины, элементы которого вычисляются по формуле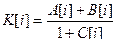 
. Если 
, то 
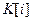принять равным нулю. Заполнение массивов A, B , C осуществить с помощью датчика случайных чисел.
#include<iostream.h>
#include<stdlib.h>
#include<conio.h>
main()
{
int i,N;
double *A,*B,*C;
cout<<"Введите N=";
cin>>N;
A=new double [N];
B=new double [N];
C=new double [N];
for(i=0; i<N; i++)
A[i]=double(random(101)-50)/10;
for(i=0; i<N; i++)
B[i]=double(random(101)-50)/10;
for(i=0; i<N; i++)
C[i]=double(random(101)-50)/10;
cout<<"Массив А:"<<endl;
for(i=0; i<N; i++)
cout<<"A["<<i<<"]="
<<A[i]<<endl;
cout<<"Массив B:"<<endl;
for(i=0; i<N; i++)
cout<<"B["<<i<<"]="
<<B[i]<<endl;
cout<<"Массив C:"<<endl;
for(i=0; i<N; i++)
cout<<"C["<<i<<"]="
<<C[i]<<endl;
double *K=new double[N];
for(i=0; i<N; i++)
if (1+C[i]) K[i]=(A[i]+B[i])/(1+C[i]);
else K[i]=0;
cout<<"Массив K:"<<endl;
for(i=0; i<N; i++)
cout<<"K["<<i<<"]="
<<K[i]<<endl;
delete []A;
delete []B;
delete []C;
delete []K;
getch();
}
Пример 2. Сформировать квадратную матрицу порядка N по правилу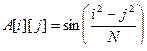 
и подсчитать количество положительных элементов в ней.
#include<iostream.h>
#include<stdlib.h>
#include<conio.h>
#include<math.h>
main()
{
int N;
cout<<"Введите размерность матрицы"<<endl;
cout<<"N=";
cin>>N;
double** A=new double* [N];
int i,j;
for (i=0; i<N; i++)
A[i]=new double [N];
for (i=0;i<N; i++)
for (j=0; j<N; j++)
A[i][j]=sin(double(i*i-j*j)/N);
for (i=0;i<N; i++){
for (j=0; j<N; j++)
cout <<A[i][j]<<" ";
cout<<endl;
}
int kol=0;
for (i=0;i<N; i++)
for (j=0; j<N; j++)
if(A[i][j]>0) kol++;
cout<<"Положительных значений = "<<kol;
getch();
}
Пример 3. Дан двумерный массив натуральных чисел размером ( 
). Не создавая дополнительных массивов, определить в каждой строке двумерного массива, какой из элементов повторяется наибольшее число раз, и найти его порядковый номер первого появления в строке. Заполнение двумерного массива осуществить с помощью ввода с клавиатуры.
#include<iostream.h>
#include<stdlib.h>
#include<conio.h>
main()
{
int N,M;
cout<<"N=";
cin>>N;
cout<<"M=";
cin>>M;
int **A=new int* [N];
int i,j;
for(int i=0; i<N; i++)
A[i]=new int [M];
for(i=0;i<N;i++)
{cout<<"Введите "<<i+1<<" строку:"<<endl;
for(j=0;j<M;j++)
{cout<<"A["<<i<<"]["<<j<<"]=";
cin>>A[i][j];
}
}
clrscr();
for(i=0;i<N;i++)
{cout<<endl;
for(j=0;j<M;j++)
cout<<A[i][j]<<" ";
}
cout<<endl;
int index, count,count_max,m;
for(i=0;i<N;i++)
{count_max=0;
index=0;
for (j=0; j<M; j++)
{count=0;
for (m=j+1; m<M; m++)
if (A[i][j]==A[i][m]) count++;
if(count>count_max) {count_max=count;
index=j;
}
}
cout<<"В "<<i+1<<"строке "
<<index<<" элемент повторяется "
<<count_max+1<<" раз"<<endl;
}
getch();
}
Варианты заданий
ЗАДАНИЕ I:
1. Заполнить массив следующим образом:
,
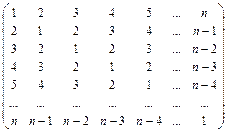n – нечетное.
2. Заполнить массив следующим образом:
,
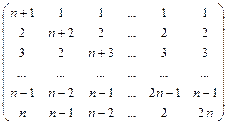n – четное.
3. Строки матрицы А(m, n) заполнить не полностью: в массиве L( m ) указать количество элементов в каждой строке. Переслать элементы матрицы построчно в начало одномерного массива Т( m ∙ n), подсчитать их количество.
4. Сформировать квадратную матрицу порядка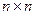 
следующим образом (n – четное):
5. Сформировать квадратную матрицу порядка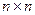 
следующим образом:
6. Матрицу М(m, n) заполнить натуральными числами от 1 до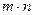 
по спирали, начинающейся в левом верхнем углу и закрученной почасовой стрелке.
7. Сформировать квадратную матрицу порядка 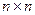следующим образом (n – четное):
8. Построить квадратную матрицу следующим образом:
9. Ввод элементов матрицы А(m, n) осуществляется в произвольном порядке тройками чисел < i, j, A ij>. Признаком конца ввода служат три нуля: <0, 0, 0>. Проверить корректность такого ввода: все ли элементы введены, нет ли попытки повторного ввода или указания несуществующих координат i и j. Указание. Разрешается выделение дополнительного (рабочего) массива такой же размерности, что и исходный массив, для хранения признаков «заполненности» элементов матрицы
10. Заполнить массив следующим образом:
,
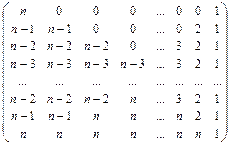n – четное.
11. Заполнить массив следующим образом:
,
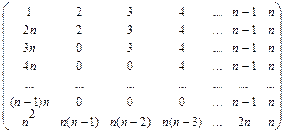n – нечетное.
12. Матрица А вводится с клавиатуры, построчно. Число строк заранее неизвестно, но различных строк не более m. Расположить строки в выделенном массиве, при этом повторяющиеся строки включать единожды.
13. Сформировать квадратную матрицу порядка 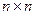следующим образом (n – четное):
14. Дано вещественное число x. Получить квадратную матрицу порядка n +1:
15. Заполнить массив следующим образом:
,
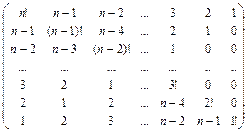n – нечетное.
16. Матрицу К(m, n) заполнить следующим образом. Элементам, находящимся на периферии (по периметру матрицы), присвоить значение 1; периметру оставшейся подматрицы — значение 2 и так далее до заполнения всей матрицы.
17. Заполнить массив следующим образом:
,
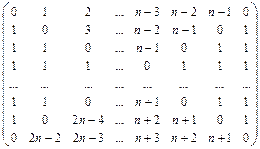n – четное.
18. Получить матрицу
19. Получить квадратную матрицу порядка n:
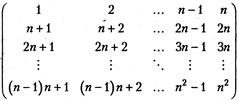
20. Матрицу А(m, n) заполнить следующим образом. Для заданных k и l элементу akl присвоить значение 1; элементам, окаймляющим его (соседним с ним по вертикали, горизонтали и диагоналям) — значение 2; элементам следующего окаймления — значение 3 и так далее до заполнения всей матрицы. Примечание. Алгоритм не изменится, если координаты элемента (несуществующего) k и l находятся за пределами матрицы.
21. Заполнить массив следующим образом:
,
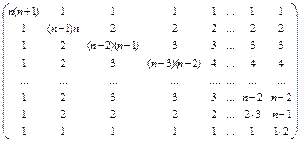n – четное.
22. Сформировать квадратную матрицу порядка 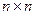следующим образом (n – четное):
23. Сформировать квадратную матрицу порядка 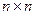следующим образом:
24. Выполнить операцию транспонирования прямоугольной матрицы А( m , n ),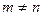 
и, не выделяя дополнительного массива для хранения результата. Матрицу А( m , n ) заполнить целочисленными случайными значениями от -100 до 100.
25. Даны вещественные числа 
. Получить квадратную матрицу порядка n:
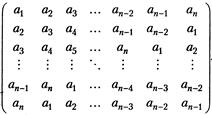
26. Сформировать квадратную матрицу порядка 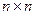следующим образом:
27. Найти произведение матриц А(m, n) и В( n , k): С( m ,k) = AxB. Матрицы А и B заполнить целочисленными случайными значениями от -10 до 10.
28. Задан одномерный массив 
. Получить вещественную квадратную матрицу порядка n:
29. Заполнить массив следующим образом:
,
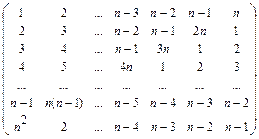n – нечетное.
30. Матрицу А(n, п) разложить на слагаемые: A = B+C+D, где В — строго нижнетреугольная, С — диагональная, D — строго верхнетреугольная матрицы того же размера. Матрицу A заполнить целочисленными случайными значениями от -20 до 20.
31. Заполнить массив следующим образом:
,
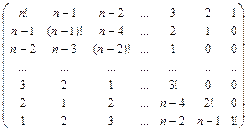n – нечетное
32. Заполнить массив следующим образом:
,
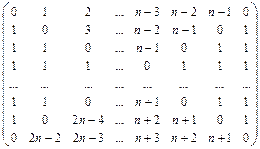n – четное.
33. Найти определитель заданной матрицы n-го порядка методом Гаусса (в любой модификации). Матрицу A заполнить вещественными случайными значениями от -20 до 20.
34. Задан одномерный массив . Получить вещественную квадратную матрицу порядка n:
35. Сформировать квадратную матрицу порядка 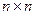следующим образом:
36. Найти матрицу, обратную заданной А(п, п), методом Гаусса (в любой модификации). Матрицу A заполнить вещественными случайными значениями от 0 до 100.
37. Сформировать квадратную матрицу порядка 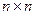следующим образом (n – четное):
38. Сформировать квадратную матрицу порядка 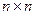следующим образом (n – четное):
39. Привести матрицу А(m, n) к трапециевидной, используя метод Гаусса, при этом не обязательно т<п. Матрицу A заполнить вещественными случайными значениями от 0 до 100.
40. Сформировать квадратную матрицу порядка 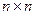следующим образом (n – четное):
41. Матрица А(п, п+1), системы линейных уравнений АХ=В приведена к верхнетреугольному виду. Найти вектор решения X последовательной подстановкой. Матрицу A заполнить вещественными значениями вводом с клавиатуры.
42. Найти ранг прямоугольной матрицы А(т, n) методом Гаусса. Матрицу A заполнить вещественными случайными значениями от 0 до 100.
43. Для заданной матрицы А(m, n) найти ее произведение на транспонированную к ней AA-1. Матрицу A заполнить целочисленными случайными значениями от -50 до 50.
44. Заполнить матрицу А(m, n) простыми числами.
ЗАДАНИЕ II:
1. Дана целочисленная матрица размера M x N. Строки матрицы назовем похожими, если совпадают множества чисел, встречающихся в этих строках. Найти количество похожих строк в матрице.
2. Дана целочисленная матрица размера M x N. Найти количество ее столбцов, все элементы которых различны.
3. Дана целочисленная матрица размера M x N. Вывести номер ее первой строки, содержащей максимальное количество одинаковых элементов.
4. Дана квадратная матрица порядка M. Найти набольшее и наименьшее значение сумм элементов матрицы, параллельных главной и побочной диагоналей.
5. Дана квадратная матрица порядка M. Найти наибольшее значение из минимальных элементов каждой диагонали, параллельной главной.
6. Дана квадратная матрица порядка M. Повернуть ее на 90, 180 и 270 градусов в положительном направлении.
7. Дана матрица размера M x N. Вывести количество столбцов, элементы которых монотонно возрастают.
8. Дана матрица размера M x N. Найти минимальный среди элементов тех строк, которые упорядочены либо по возрастанию, либо по убыванию.
9. Дана целочисленная матрица размера M x N. Найти элемент, являющийся максимальным в своей строке и минимальным в своем столбце.
10. Дана матрица размера M x N. Элемент называется локальным минимумом, если он меньше всех окружающих его элементов. Заменить все локальные минимумы данной матрицы на 0.
11. Дана матрица размера M x N. Поменять местами ее столбцы так, чтобы их минимальные элементы образовывали возрастающую последовательность.
12. Дана матрица А размером M x N.. Определить k — количество особых элементов массива А, считая его элемент особым, если он больше суммы остальных элементов его столбца.
13. Элемент матрицы назовем седловой точкой, если он является наименьшим в своей строке и одновременно наибольшим в своем столбце или, наоборот, является наибольшим в своей строке и наименьшим в своем столбце. Для заданной целой матрицы размером M x N напечатать индексы всех ее седловых точек.
14. Задана матрица размером M x N. Найти максимальный по модулю элемент матрицы. Переставить строки и столбцы матрицы таким образом, чтобы максимальный по модулю элемент был расположен на пересечении i – й строки и k – то столбца.
15. Дана целая квадратная матрица n - го порядка. Определить, является ли она магическим квадратом, т.е. такой, в которой суммы элементов во всех строках и столбцах одинаковы. Получить транспонированную матрицу. Сформировать одномерный массив из ее диагональных элементов. Найти след матрицы, суммируя элементы одномерного массива.
16. Квадратная матрица, симметричная относительно главной диагонали, задана верхним треугольником в виде одномерного массива. Восстановить исходную матрицу и напечатать по строкам.
17. Дана квадратная целочисленная матрица порядка п. Сформировать результирующий одномерный массив, элементами которого являются строчные суммы тех строк, которые начинаются с k идущих подряд положительных чисел.
18. Дана целочисленная матрица размером M x N. Элемент матрицы называется среднестатистическим по k – му параметру, если на нем достигается минимум модуля разности среднего арифметического чисел из k -го столбца и k – ой строки. Элемент называется самым средним, если он является среднестатистическим по самому большому количеству параметров. В данной матрице определить пять самых средних элементов.
19. Прямоугольное поле разбито на M x N квадратных клеток. Некоторые клетки покрашены в черный цвет. Известно, что все черные клетки могут быть разбиты на несколько непересекающихся и не имеющих общих вершин черных прямоугольников. Считая, что цвета клеток даны в виде массива M x N, значения элементов которого равны либо 0, либо 1. Подсчитать число черных прямоугольников, о которых шла речь. Число действий должно быть порядка M x N.
Указание. Число прямоугольников равно числу их левых верхних углов. Является ли клетка верхним углом, можно узнать, посмотрев на ее цвет, а также цвет верхнего и левого соседей. (Не забудьте, что их может не быть, если клетка с краю.)
20. Даны квадратная таблица A [ N , N ] и число М< N. Для каждого квадрата размером M x M этой таблице вычислить сумму стоящих в нем чисел.
Указание. Сначала для каждого горизонтального прямоугольника размером Мх 1 вычислить сумму стоящих в нем чисел. (При сдвиге такого прямоугольника по горизонтали на 1 нужно добавить одно число и одно вычесть.) Затем, используя эти суммы, вычислить суммы в квадратах. (При сдвиге квадрата по вертикали добавляется полоска, а другая полоска убавляется.)
21. Среди тех строк и столбцов целочисленной матрицы, которые содержат только нечетные элементы, найти строку или столбец с максимальной и минимальной суммой модулей элементов.
22. Подсчитать количество строк заданной целочисленной матрицы NxN , являющихся перестановкой чисел 1, 2, ..., N (т.е.содержащих каждое из чисел 1, 2, ..., N ровно один раз).
23. Среди строк и столбцов заданной целочисленной матрицы, содержащих только такие элементы, которые по модулю не больше 10, найти столбец или строку с минимальным и максимальным произведением элементов.
24. Целочисленным массивом кодируется поле, на котором расположены несколько прямоугольников. Прямоугольники не накладываются друг на друга и не соприкасаются. Разные прямоугольники состоят из разных значений. Один и тот же прямоугольник не может состоять из различных значений. Пустые квадраты поля кодируются значением 0. Подсчитать число прямоугольников разных значений.
Пример :
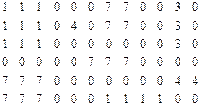
Для этого поля программа должна выдать ответ:
1-прямоугольников: 2
7-прямоугольников: 3
3-прямоугольников: 1
4-прямоугольников: 2
25. Характеристикой столбца целочисленной матрицы назовем сумму модулей его отрицательных нечетных элементов. Переставляя столбцы заданной матрицы, расположить их в соответствии с ростом характеристик.
26. Для заданной квадратной матрицы найти такие k , что k -я строка матрицы совпадает с k -м столбцом.
27. Найти максимальный элемент среди всех элементов тех строк заданной матрицы, которые упорядочены (либо по возрастанию, либо по убыванию).
28. Расстояние между k – й и l – й строками квадратной матрицы А ( NxN ) определяется как
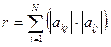
Найти строки заданной матрицы, максимально удаленные друг от друга.
29. Определить, является ли заданная матрица ортонормированной, т. е. равно ли скалярное произведение каждой пары различных строк (столбцов) нулю.
30. Определить номера строк матрицы, в которых знаки элементов чередуются.
31. В целочисленной матрице M x N требуется каждый элемент заданной матрицы заменить минимальным элементом, выбираемым среди элементов, стоящих не ниже и не правее этого элемента, включая его значение.
32. Даны мозаичные изображения замочной скважины и ключа. Пройдет ли ключ в скважину? То есть даны матрицы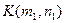 
и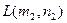 
, 
, 
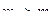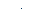, состоящие из нулей и единиц. Проверить можно ли наложить матрицу L на матрицу K (без поворота, разрешается только сдвиг) так, чтобы каждой единице матрицы L соответствовал нуль матрицы K, и если можно, то как (на сколько и в каком направлении следует подвинуть матрицу L по матрице K до выполнения условия)?
33. В целочисленной матрице M x N каждый элемент (кроме граничных) заменить суммой непосредственно примыкающих к нему элементов по вертикали, горизонтали и диагонали.
34. Матрица M x N состоит из нулей и единиц. Найти в ней самую длинную цепочку подряд стоящих нулей по горизонтали, вертикали или диагонали.
35. Дана целочисленная матрица размером M x N. Найти все числа, каждое из которых встречается в каждой строке матрицы, и все числа, повторяющиеся более чем в одном столбце матрицы.
36. Клеточное поле размером M x N есть результат игры в крестики и нолики на “бесконечном поле”. Проверить, не закончена ли игра выигрышем. Считается, игра закончена, если на поле найдется по горизонтали, вертикали или диагонали цепочка, состоящая подряд из 5 крестиков или ноликов. (Значение 0 соответствует нолику, 1 соответствует крестику, 2 – пустой клетки.)
37. Дана целочисленная матрица размером M x N, состоящая из нулей и единиц. Найти квадрат наибольшего значения (квадратную подматрицу), состоящий из нулей или единиц.
38. Дана целочисленная матрица размера M x N. Различные столбцы матрицы назовем похожими, если совпадают множества чисел, встречающихся в этих столбцах. Найти количество столбцов, похожих на последний столбец.
39. Дана целочисленная матрица размера M x N. Найти количество ее строк, все элементы которых различны.
40. Дана целочисленная матрица размера M x N. Вывести номер его последнего столбца, содержащего максимальное количество одинаковых элементов.
41. Дана квадратная матрица порядка M. Вывести максимальные из элементов каждой ее диагонали, параллельной побочной.
42. Дана матрица размера M x N. Вывести количество строк, элементы которых монотонно убывают.
43. Дана матрица размера M x N. Найти максимальный среди элементов тех столбцов, которые упорядочены либо по возрастанию, либо по убыванию. Если такие столбцы отсутствуют, то вывести 0.
44. Дана матрица размера M x N. Элемент называется локальным максимумом, если он больше всех окружающих его элементов. Заменить все локальные максимумы данной матрицы на 0.
45. Дана матрица размера M x N. Поменять местами ее строки так, чтобы их максимальные элементы образовывали убывающую последовательность.
46. Дана целочисленная матрица размером M x N. Элемент матрицы называется уникальным по k – му параметру, если на нем достигается максимум модуля разности среднего арифметического чисел из k -го столбца и k – ой строки. Элемент называется самым уникальным, если он является среднестатистическим по самому большому количеству параметров. В данной матрице определить пять самых средних элементов.
47. Каждый элемент а( i , j ) матрицы A ( m , n ) заменить суммой элементов подматрицы A ’( i , j ), расположенной в правом нижнем углу матрицы. Заполнение начать с конца матрицы.
Лабораторная работа №6
Дата: 2019-02-02, просмотров: 845.
