С.А. Дьяконица
Д.С. Семенов
ОСНОВЫ ПРОГРАММИРОВАНИЯ НА ЯЗЫКЕ C ++
Методические указания к лабораторным работам по дисциплине
Лабораторный практикум
Братск
УДК 681.3.06
Основы программирования на языке С++: Методические указания к лабораторным работам / С.А. Дьяконица, Д.С. Семенов. – Братск: БрГУ, 2007. – с.
Содержат указания к выполнению цикла лабораторных работ, а также основным понятиям, принципам и приемам разработки программ на языке С++.
Предназначены для студентов дневной, заочной форм обучения и обучающихся по сокращенным образовательным программам специальности.
Рецензент:
к.т.н. Крумин О.К.А.Н. Емцев, канд. техн. наук,
профессор кафедры систем электроснабжения
Печатается по решению издательско-библиотечного совета
| 665709, Братск, ул. Макаренко, 40, Братский государственный ун-т Тираж 100 экз. Заказ |
| |
СОДЕРЖАНИЕ
| Введение…………………………………………..……............ | 4 |
| Лабораторная работа №1 Программирование алгоритмов линейной структуры………………………….. | 5 |
| Лабораторная работа №2 Программирование алгоритмов разветвляющейся структуры……………… | 36 |
| Лабораторная работа №3 Программирование алгоритмов циклической структуры……………………… | 58 |
| Лабораторная работа №4 Программирование алгоритмов над статическими массивами……………… | 79 |
| Лабораторная работа №5 Программирование алгоритмов над многомерными динамическими массивами…………….... | 106 |
| Лабораторная работа №6 Программирование алгоритмов над массивами символов……………………... | 135 |
| Список используемых источников………………………… | 151 |
| Приложение 1. Стандартные библиотеки функций языка Си……………………………………………………… | 152 |
| Приложение 2. Таблица ASCII – кодов символов……… | 172 |
ВВЕДЕНИЕ
Практическому программированию нельзя научиться теоретически, без решения задач на ЭВМ. Целью практикума является закрепление теоретического материала, изучение технических приемов составления и отладки программ, привитие навыков практического программирования на языке Си++, изучение и использование наиболее важных численных методов.
Практикум предусматривает прохождение всех ступеней начального программирования: понимание задачи, разработку алгоритма, составление и подготовку программы к работе на ЭВМ, отладку программы, счет и анализ результатов. Он может быть использован, как студентами, самостоятельно изучающими программирование, так и преподавателями для организации лабораторных работ.
Практикум включает 6 лабораторных работ, каждая из которых посвящена конкретной теме.
В начале каждой лабораторной работы приведены теоретические сведения с примерами типовых задач. Все примеры написаны в стиле ANSI и протестированы с использованием компилятора Borland C++. Разбор этих решений поможет в написании собственных программ, в освоении некоторых полезных технических приемов, приобретении определенного стиля программирования.
Лабораторная работа №1
Программирование алгоритмов линейной структуры
Цель работы: выработать практические навыки работы с системой программирования языка Си/Си++, научиться создавать, вводить в компьютер, выполнять и исправлять простейшие программы на языке Си/Си++ в режиме диалога, познакомиться с диагностическими сообщениями компилятора об ошибках при выполнении линейных программ.
Рис.1 Структура процесса компиляции
Особенности выполнения перечисленных действий зависят от конкретного компилятора языка Си/Си++ и той операционной системы, в которой он работает. Технические подробности можно изучить по документации для конкретного программного продукта. Например, при работе с интегрированными средами фирмы Borland необходимая информация может быть получена из руководств пользователя.
В простейшем случае программа на языке Си и Си++ представляет собой набор описаний и определений, и состоит из набора функций. Среди этих функций всегда должна быть функция с именем main (для консольных программ) или WinMain (для программ в 32 – разрядных операционных систем). Данные функции являются точками входа и выхода, и без них программа не может быть выполнена. Если функция не возвращает никакого значения в результате своего выполнения, то перед именем функции помещается служебное слово void, обозначающее тип отсутствия значения. Также каждая функция должна иметь набор параметров, если параметры отсутствуют, то скобки оставляют пустыми или в них указывается void.
За заголовком размещается тело функции. Тело функции - это последовательность определений, описаний и исполняемых операторов, заключенных в фигурные скобки. Ниже приведен листинг простейшей программы на языке Си/Си++, вычисляющая объем цилиндра по радиусу и высоте, значения которых вводятся с клавиатуры.
// подключение средств консольного потокового ввода/вывода
#include <iostream.h>
//подключение математических функций
#include <math.h>
/* главная функция программы */
void main ()
{
// объявление переменных
int r,v,h;
//вывод на экран
cout <<”\nВведите радиус и высоту цилиндра:";
//вывод на экран
cin >> r >> h;
//ввод значений с клавиатуры
v=M_PI*r*r*h;
cout <<"\nобъем цилиндра = " << v;
}
Основные элементы синтаксиса языка Си/Си++
Основные синтаксические правила и записи программ на языке Си/Си++ сводятся к следующему:
§ Прописные и строчные буквы считаются разными символами. При записи идентификатора могут использоваться латинские буквы, цифры и символ подчеркивания (_). Идентификатор не может начинаться с цифры и содержать в себе пробельный символ. Длина идентификатора не ограничена.
§ Пробельные символы могут размещаться в любом месте текста программы, но не внутри идентификатора.
§ Комментарии заключаются в скобки вида: /* текст комментария */ и могут вводиться в любом месте программы и занимать любое количество строк. Еще один способ введения комментария – размещение его после символов двойного слэша (//). Такой комментарий должен занимать конец строки и не должен переходить на следующую строку.
§Каждое (почти каждое) предложение языка кончается символом точка с запятой (;).
§ В строке могут размещаться несколько операторов.
§ Фигурные скобки выделяют составной оператор ({}). Все операторы, заключенные между такими скобками воспринимаются как один оператор.
§ Все используемые типы, переменные, константы, функции должны быть описаны или объявлены до их первого использования. Объявления могут встречаться в любом месте программы.
Также ряд слов в языке Си/Си++ имеет особое значение и не может использоваться в качестве идентификаторов. Такие зарезервированные слова называются служебными. Полный список служебных слов зависит от реализации языка, однако существует список основных служебных слов, определенный стандартом языка Си/Си++:
asm auto bad_cast
bad_typeid bool break
Case catch char
class const const_cast
Else enum extern
Float for friend
Goto if inline
Xalloc
Типы данных
Концепция типов данных является важнейшей стороной любого языка программирования. С типом величины связаны три ее свойства: форма внутреннего представления, множество принимаемых значений и множество допустимых операций. Особенность языка Си состоит в большом разнообразии типов, схематически представленном на рис. 2.

Рис. 2 Структура типа данных языка Си++
В таблице 1 приведены служебные слова основных арифметических типов данных, их размеры в памяти и диапазоны допустимых значений.
Пользователь также может вводить в программу свои собственные типы. Объявления пользовательских типов могут делаться в различных местах кода программы. Их место объявления влияет на область видимости вводимого типа. Синтаксис объявления пользовательского типа является следующий:
typedef определение_типа идентификатор;
Где идентификатор – это вводимое пользователем имя нового типа, а определение_типа – описание этого типа. Например, запись
typedef double Ar 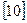 ;
;
объявляет тип пользователя с именем Ar как массив из 10 действительных чисел. В дальнейшем на этот тип можно ссылаться при объявлении переменных. Например:
Ar A = 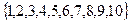 .
.
Таблица 1
Арифметические типы данных
| тип данных | название | размер, бит | диапазон значений |
| unsigned char | беззнаковый малый целый или коды символа | 8 | 0 . . 255 |
| char | малый целый или код символа | 8 | -128 . . 127 |
| unsigned int | беззнаковый целый | 16 | 0 . . 65535 |
| short int (short) | короткий целый | 16 | -32768 . . 32767 |
| unsigned short | беззнаковый короткий целый | 16 | 0 . . 65535 |
| int | целый | 16 | -32768 . . 32767 |
| unsigned long | беззнаковый длинный целый | 32 | 0 . . 4294967295 |
Продолжение табл.1
| тип данных | название | размер, бит | диапазон значений |
| long | длинный целый | 32 | -214748348 . . 2147483647 |
| float | вещественный одинарной точности | 32 | 3.4Е-38 . . 3.4Е+38 |
| double | вещественный двойной точности | 64 | 1.7Е-308 . . 1.7Е+308 |
| long double | вещественный максимальной точности | 80 | 3.4Е-4932 . . 1.1Е+4932 |
Операции присваивания
| Обозначение | Операция | Пример |
| = | Присваивание | X=Y |
| += | Присваивание со сложением | Х+=Y |
| -= | Присваивание с вычитанием | Х-=Y |
| *= | Присваивание с умножением | Х*=Y |
| /= | Присваивание с делением | Х/=Y |
| %= | Присваивание остатка целочисленного деления | Х%=Y |
| <= | Присваивание со сдвигом влево | Х<=Y |
| >= | Присваивание со сдвигом вправо | Х>=Y |
| &= | Присваивание с поразрядной операцией И | Х&=Y |
| ^= | Присваивание с поразрядной операцией исключающее ИЛИ | Х^=Y |
| |= | Присваивание с поразрядной операцией ИЛИ | Х|=Y |
Помимо простой операции присваивания (=) все прочие являются составными операциями. Они присваивают первому операнду результат применения соответствующей простой операции, указанной перед символом (=), к первому и второму операндам. Например, выражение X+=Y эквивалентно выражению X=X+Y, но записывается компактнее и может выполнятся быстрее. Аналогично определяются и другие операции присваивания: X%=Y эквивалентно X=X%Y и т.д.
При записи составных операций присваивания между символом операции и знаком равенства пробел не допускается.
В операциях присваивания первый операнд не может быть нулевым указателям.
Пример программы, реализующей алгоритм линейной структуры
Заданы вершины треугольника А(x1,y1), B(x2,y2), C(x3,y3). Вычислить длину медианы, проведенной из А.
//Подключение средств консольного потокового
// ввода / вывода
#include<iostream.h>
//Подключение математических функций
#include<math.h>
//Подключение библиотеки для использования функции
//getch()
#include<conio.h>
//главная функция
main()
{
//Объявление переменных для задания координат
// точек треугольника
double Ax,Ay,Bx,By,Cx,Cy;
//Ввод координат точки А
cout<<"Введите координаты точки А:"<<endl;
cout<<"x=";
cin>>Ax;
cout<<"y=";
cin>>Ay;
//Ввод координат точки B
cout<<"Введите координаты точки B:"<<endl;
cout<<"x=";
cin>>Bx;
cout<<"y=";
cin>>By;
//Ввод координат точки C
cout<<"Введите координаты точки C:"<<endl;
cout<<"x=";
cin>>Cx;
cout<<"y=";
cin>>Cy;
//Объявление переменных, в которых будут
//находится длины сторон
double ab,bc,ca;
//Вычисление стороны AB
ab=sqrt((Ax-Bx)*(Ax-Bx)+(Ay-By)*(Ay-By));
//Вычисление стороны BC
bc=sqrt((Bx-Cx)*(Bx-Cx)+(By-Cy)*(By-Cy));
//Вычисление стороны CA
ca=sqrt((Cx-Ax)*(Cx-Ax)+(Cy-Ay)*(Cy-Ay));
//Объявление переменной для медианы
// и вычисление ее через длины
//сторон треугольника
double M=sqrt(2*ab*ab+2*ca*ca-bc*bc)/2;
//Вывод значения длины медианы
cout<<"Длина медианы, из точки А равна:”
<<M<<endl;
cout<<"Для завершения нажмите любую клавишу";
getch();
}
Примечание: Чтобы сразу после окончания работы программы окно, в котором программа работала, не было автоматически перекрыто другим окном, например окном редактора текста среды разработки, в конце программы желательно использовать функцию getch(), которая приостанавливает выполнение программы до тех пор, пока не будет нажата любая клавиша.
Варианты заданий
1. Заданы координаты трех вершин треугольника (х1, у1), (х2, у2),(x3, y3). Найти его периметр и площадь.
2. Длина отрезка задана в дюймах (1 дюйм = 2,54 см). Перевести значение длины в метрическую систему, то есть выразить ее в метрах, сантиметрах и миллиметрах. Например: 21 дюйм = 0 м 53 см 3.4 мм.
3. В такси одновременно сели три пассажира. Когда вышел первый пассажир, на счетчике было p 1 рублей; когда вышел второй p 2 рублей. Сколько должен был заплатить каждый пассажир, если по окончании поездки счетчик показал p 3 рублей? Плата за посадку составляет p 0 рублей.
4. Дана сторона равностороннего треугольника. Найти радиусы и площади вписанной и описанной окружностей.
5. Коммерсант, имея стартовый капитал k рублей, занялся торговлей, которая ежемесячно увеличивает капитал на р%. Через сколько лет, он накопит сумму s, достаточную для покупки собственного магазина?
6. Треугольник задан величинами своих углов и радиусом описанной окружности. Найти стороны треугольника.
7. Селекционер вывел новый сорт зерновой культуры и снял с опытной делянки k кг семян. Посеяв 1 кг семян, можно за сезон собрать р кг семян. Через сколько лет селекционер сможет засеять новой культурой поле площадью s га, если норма высева n кг/га?
8. Найти площадь равнобедренной трапеции с основаниями а и b и углом a при большем основании а.
9. Треугольник задается координатами своих вершин на плоскости: A (x1, y1), B(x2, у2), С(х3, у3). Найти длину и основание высоты, опущенной из вершины А на сторону ВС.
10. За первый год производительность труда на предприятии возросла на p1 %, за второй и третий — соответственно на р2 и р3 %. Найти среднегодовой прирост производительности (в процентах).
11. Найти сумму членов арифметической прогрессии, если известны ее первый член, знаменатель и число членов прогрессии.
12. Заданы координаты точки подвески математического маятника А( x , y , z ) и координаты одной из точек его наивысшего подъема B(x1, y1, z1). Найти координаты самой низкой точки траектории и другой наивысшей точки подъема.
13. Найти (в радианах и в градусах) все углы треугольника со сторонами а, b, с.
14. Русские неметрические единицы длины: 1 верста = 500 саженей; 1 сажень = 3 аршина; 1 аршин = 16 вершков; 1 вершок = 44,45 мм. Длина некоторого отрезка составляет р метров. Перевести ее в русскую неметрическую систему.
15. Составить программу перевода радианной меры угла в градусы, минуты и секунды.
16. Вычислить высоты треугольника со сторонами а, b, с.
17. У квадрата ABCD на плоскости известны координаты двух противоположных вершин — точек А и С. Найти координаты точек В и D. Примечание: расположение квадрата произвольно, его стороны не обязательно параллельны координатным осям.
18. Вычислить медианы треугольника со сторонами а, b, с.
19. Автомобиль потребляет l литров топлива. Владелец автомобиля приобрел новый карбюратор, который экономит n % топлива, новую систему зажигания, которая экономит m % топлива, и поршневые кольца, экономящие k % топлива. Найти фактическую экономию топлива в процентах и количество потребляемого топлива.
20. Вычислить биссектрисы треугольника со сторонами а, b, с.
21. Треугольник задается координатами своих вершин на плоскости: A(x1, y1), B(x2, у2), С(х3, у3). Найти точку пересечения биссектрис треугольника ABC (центр вписанной в него окружности).
22. Дано натуральное число Т, которое представляет длительность прошедшего времени в секундах. Вывести данное значение длительности в часах, минутах и секундах в следующей форме: НН ч ММ мин SS с.
23. Заданы два вектора с координатами (x 1, y 1, z 1) и (x 2, y 2, z 2). Определить угол между векторами.
24. Вычислить площадь и периметр правильного N-угольника, описанного около окружности радиуса R (рассмотреть N — целого типа, R — вещественного типа).
25. Задан вектор с координатами (х, у, z). Найти углы наклона этого вектора к координатным осям.
26. Найти площадь круга, вписанного в треугольник с заданными сторонами.
27. Треугольник задается координатами своих вершин на плоскости: A (x1, y1), B(x2, у2), С(х3, у3). Найти внутренние углы треугольника ABC (в градусах).
28. Найти площадь круга, описанного около треугольника с заданными сторонами.
29. Треугольник задан величинами своих углов и радиусом вписанной окружности. Найти стороны треугольника.
30. Вычислить площадь и периметр правильного N-угольника, вписанного в окружность радиуса R (рассмотреть N — целого типа, R — вещественного типа).
31. Найти объем пирамиды, построенной на векторах А, В, С, как на сторонах. Вектора заданы координатами (х, у, z).
32. Определить токи на резисторах R1..R7 электрической схемы.
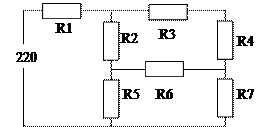 |
32. Определить напряжение на резисторах R1..R7 электрической схемы.
 |
34. Определить число месяцев, через которое начальная сумма вклада в банке увеличится в три раза. Программа запрашивает ввод начальной суммы и ежемесячную процентную ставку.
35. Треугольник задается координатами своих вершин на плоскости: A (x1, y1), B(x2, у2), С(х3, у3). Найти точку D, симметричную точке А относительно стороны ВС.
36. Определить сумму денежного вклада через несколько месяцев при ежемесячной процентной ставке. Программа запрашивает ввод начальной суммы, ежемесячной процентной ставки и срока вклада.
37. Заданы координаты трех вершин треугольника (х1, у1, z 1), (х2, у2, z 2),(x3, y3, z 3). Найти его периметр и площадь.
38. Определить координаты трех точек A, B, C пересечения фигур – двух окружностей с центрами (2,1) и (-5,0) и радиусами, равными 5, и прямой (с углом наклона a.).
 |
39. Определить координаты четырех точек пересечения A, B, C , D прямой y = kx +1 с окружностью (радиус равен 5) и квадратичной параболы y 2 =- x +5.

| 40 - 45. Дан прямоугольный треугольник ABC (g = 90°), для которого определен следующий набор характерных параметров (рис.3 ): а, b , с — стороны треугольника; a , b — острые углы (в градусах); h — высота, опущенная на гипотенузу с; S — площадь; Р — периметр треугольника. По двум заданным параметрам вычислить все остальные. Сочетания данных параметров: 40. a, b; 41. a, c; 42. a, h; 43. b, a; 44. h, b; 45. c, b. | 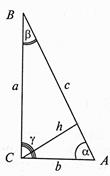 Рис. 3
Рис. 3
| |
| 46.– 50. Дан произвольный треугольник ABC (рис. 4), для которого определен следующий набор характерных параметров: а, b, с - стороны треугольника; a , b , g — углы (в градусах); h — высота, опущенная на сторону с; S — площадь; Р — периметр треугольника. По трем заданным параметрам вычислить все остальные. Сочетания данных параметров: 46. a , b , g ; 47. c , a , b ; 48. h , c , a ; 49. S , h , b ; 50. S , c , a ; |
| |
Рис. 4
Лабораторная работа №2
Структуры
Цель работы: выработать практические навыки работы с системой программирования языка Си++, познакомиться с диагностическими сообщениями компилятора об ошибках при выполнении программ, реализующих алгоритмическую структуру “ветвление” (операторы if , switch).
Основные теоретические сведения
Основные операции отношения
| Обозначение | Операция | Пример |
| == | Равно | A==B |
| != | Не равно | Х!=Y |
| < | Меньше чем | Х<Y |
| > | Больше чем | C>0 |
| <= | Меньше или равно | A<=I |
| >= | Больше или равно | Х>=Y |
Операнды должны иметь совместимые типы, за исключением целых и действительных типов, которые могут сравниваться друг с другом.
Логические операции
Логические операции принимают в качестве операндов выражения скалярных типов и возвращают результат булева типа: true или false. В С++ любое выражение, имеющее некоторое значение, может использоваться в логических операциях. Так если значение выражения 0, то оно трактуется как false, любое другое значение трактуется как true.
Таблица 9
Условный оператор выбора
Оператор if предназначен для выполнения тех или иных действий в зависимости от истинности или ложности некоторого условия. Условие задается выражением, имеющим результат булева типа.
Оператор имеет две формы:
1) i f(условие)оператор;
Скобки, обрамляющие условие, обязательны.
Условием может быть выражение, преобразуемое в булев тип. Если условие истинно, то указанный в конструкции оператор выполняется. В противном случае управление сразу передается следующему за конструкцией if оператору.
2) if (условие) оператор1;
else оператор2;
Если условие возвращает true, то выполняется первый из указанных операторов, в противном случае выполняется второй оператор. Обратите внимание, что в конце первого оператора перед ключевым словом else ставится точка с запятой.
При вложенных конструкциях if могут возникнуть неоднозначности в понимании того, к какой из вложенных конструкций if относится элемент else. Компилятор всегда считает, что else относится к последней из конструкций if, в которой не было раздела else. Например,
if(условие1)
if(условие2)
оператор1;
else оператор2;
else будет отнесено компилятором ко второй конструкции if, т.е. оператор2 будет выполняться в случае, если первое условие истинно, а второе ложно.
Если же вы хотите отнести else к первому if, это надо записать в явном виде с помощью фигурных скобок:
if(условие1)
{
if(условие2) оператор1;
}
else оператор2;
В конструкциях в качестве оператор, оператор1 и оператор2 понимается использование одного оператора или выражения. Если необходимо выполнение нескольких операторов, то следует использовать составной оператор.
Поскольку в Си++ любое арифметическое значение может преобразовываться к булеву типу, т.е. если значение выражения 0, то оно трактуется как false, а любое другое значение трактуется как true. То в условии можно использовать практически любые арифметические выражения. Например:
int a,b,c;
…
if(a–b/c) …;
В данном случае условие if(a–b/c) будет false, если результат выражения a-b/c буде нуль, и условие будет true при всех остальных результатах выражения.
Так же, следует предостеречь от довольно распространенной ошибки: случайного применения вместо операции эквивалентности (==) операции присваивания (=). Например, если по ошибке вместо оператора
if (A==2) …;
используется оператор
if (A=2) …;
то это не будет расценено как синтаксическая ошибка. Результат операции А=2 будет трактоваться как true независимо от того, чему было равно значение переменной А до выполнения этого ошибочного оператора. К тому же выполнение этого оператора приведет к изменению переменной.
Примеры, реализующие алгоритмы разветвляющейся структуры
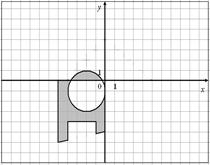
Пример 1. Для данной области (рис. 5.а) составить программу, которая определяет принадлежность точки с координатами (x,y) закрашенной области:
а) b)
Рис. 5
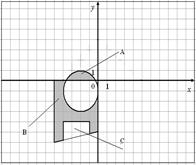
Разобьем закрашенную область на три фигуры (рис. 5.б) и для каждой фигуры приведем ограничения в виде неравенств.
Фигура A ограничена осью абсцисс (y =0) и окружностью с центром в точке (-2;-1) и радиусом R =2. Чтобы точка принадлежала фигуре A нужно выполнение следующих условий: 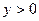 И
И 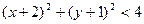 .
.
Фигура B ограничена осью абсцисс (y =0), осью ординат (x =0), прямой, проходящей через точки (-5;-6) и (0;-5), а также окружностью с центром в точке (-2;-1) и радиусом R =2. Чтобы точка принадлежала фигуре B нужно выполнение следующих условий: 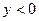 И
И 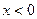 И
И 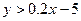 И
И 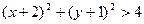 .
.
Фигура C ограничена прямыми, параллельными осям координат (y =-4), (x =-5), (x =-1), а также прямой, проходящей через точки (-5;-6) и (0;-5). Чтобы точка принадлежала фигуре C нужно выполнение следующих условий: 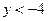 И
И  И
И 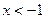 И
И 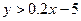 .
.
Для того, чтобы точка принадлежала закрашенной области, необходимо выполнение одного из двух условий:
1) чтобы точка попала в область фигуры A;
2) чтобы точка попала в область фигуры В и одновременно не попала в область фигуры C.
В общем случае условие принадлежности закрашенной области выглядит следующим:
A ИЛИ ( B И (НЕ С))
Листинг программы, выполняющий данное задание:
#include<iostream.h>
#include<conio.h>
main()
{
double x,y;
cout <<"Введите координаты точки:"<<endl;
cout <<"x=";
cin >> x;
cout <<"y=";
cin >> y;
int A,B,C;
//проверка условий попадания в область фигуры A
A=(y>0)&&((x+2)*(x+2)+(y+1)*(y+1)<4);
//проверка условий попадания в область фигуры B
B=(y<0)&&(x<0)&&(y>0.2*x-5)
&&((x+2)*(x+2)+(y+1)*(y+1)>4);
//проверка условий попадания в область фигуры C
C=(y<-4)&&(x>-4)&&(x<-1);
//проверка условия попадания в закрашенную область
//если A ИЛИ ( B И (НЕ С))
if (A||(B&&(!C)))
cout << "Точка принадлежит заданной области";
else
cout << "Точка не принадлежит заданной области";
getch();
}
Пример 1. Составить программу, которая по введенным двум числам и одному из знаков (+, -, *, /), осуществит результат соответствующего арифметического действия.
#include<iostream.h>
#include<conio.h>
main()
{
double x,y;
cout <<"Введите число X=";
cin >>x;
cout <<"Введите число Y=";
cin >>y;
char op;
cout <<"Введите арифметическую операцию:";
cin >>op;
switch (op){
case '+': cout <<"X+Y="<<x+y;
break;
case '-': cout <<"X-Y="<<x-y;
break;
case '*': cout <<"X*Y="<<x*y;
break;
case '/': cout <<"X/Y="<<x/y;
break;
default: cout <<"Неизвестная операция!";
}
getch();
}
Варианты заданий
ЗАДАНИЕ I :
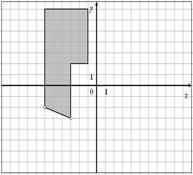
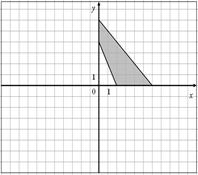
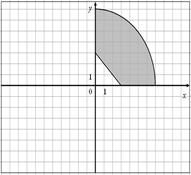
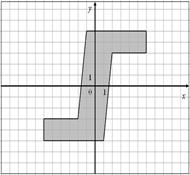
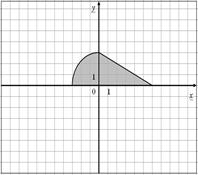
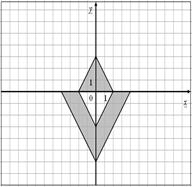
Для данных областей составить программу, которая определяет принадлежность точки с координатами (x,y) закрашенной области:
1.
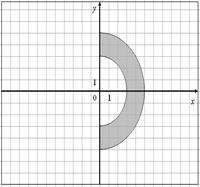
| 2.
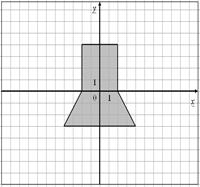
|
3.
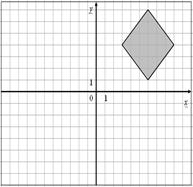
| 4.
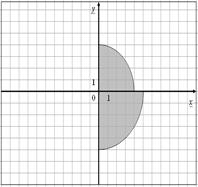
|
5.
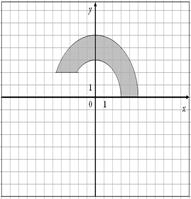
| 6.
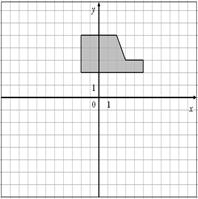
|
7.
| 8.
|
9.
| 10.
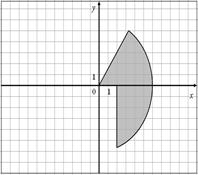
|
11.
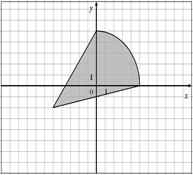
| 12.
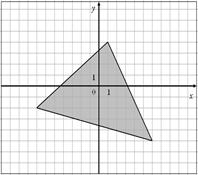
|
13.
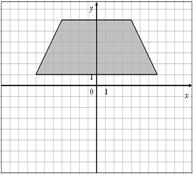
| 14.
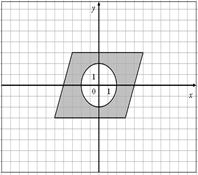
|
15.
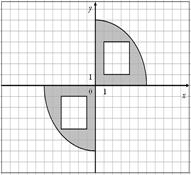
| 16.
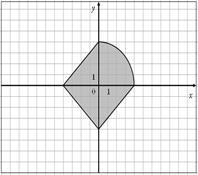
|
17.
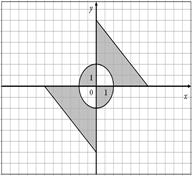
| 18.
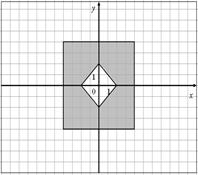
|
19.
| 20.
|
21.
| 22.
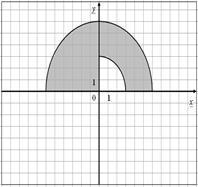
|
23.
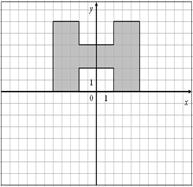
| 24.
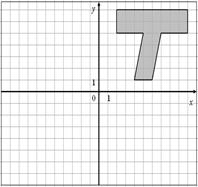
|
25.
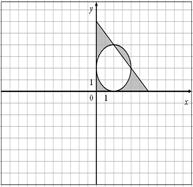
|
26.
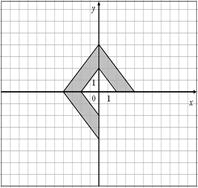
|
27.
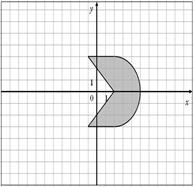
| 28.
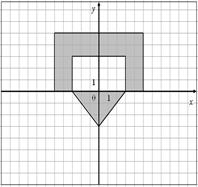
|
29.
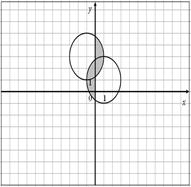
| 30.
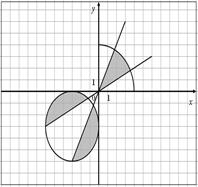
|
31.
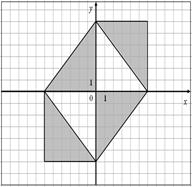
|
32.
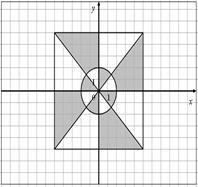
|
33.
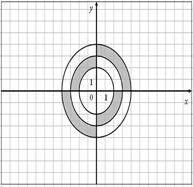
| 34.
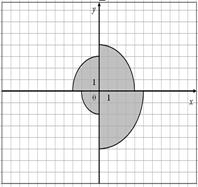
|
35.
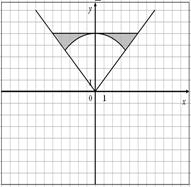
| 36.
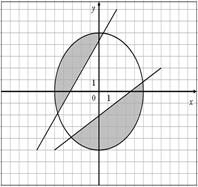
|
37.
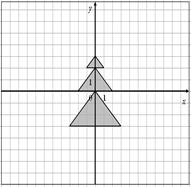
|
38.
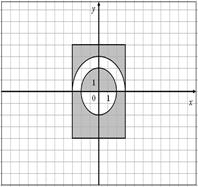
|
39.
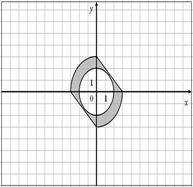
| 40.
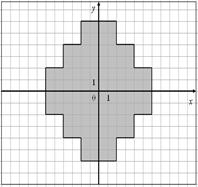
|
41.
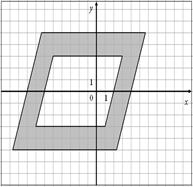
| 42.
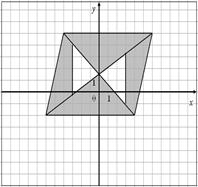
|
43.
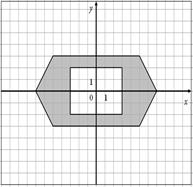
|
44.
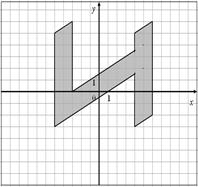
|
45.
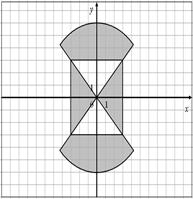
| 46.
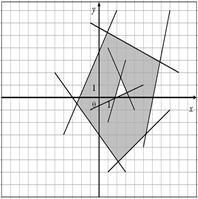
|
47.
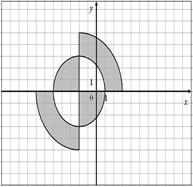
| 48.
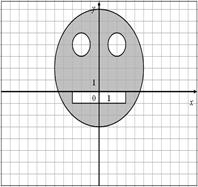
|
49.
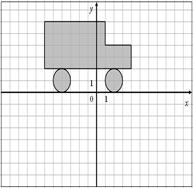
| 50.
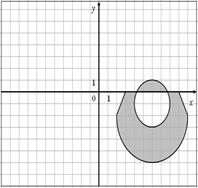
|
ЗАДАНИЕ 2:
Для всех вариантов заданий, при организации ветвления в программе, следует использовать конструкцию множественного выбора switch … case .
1. Написать программу расчета площади фигуры по названию (треугольник, квадрат, прямоугольник, ромб, трапеция и окружность). Для вычисления площади, программа должна производить запрос необходимых параметров исходя из выбранной фигуры.
2. Написать программу расчета периметра фигуры по названию (треугольник, квадрат, прямоугольник, ромб, трапеция и окружность). Для вычисления периметра, программа должна производить запрос необходимых параметров исходя из выбранной фигуры.
3. Написать программу расчета объема фигуры по названию (шар, конус, усеченный конус, куб, параллелепипед и цилиндр). Для вычисления объема, программа должна производить запрос необходимых параметров исходя из выбранной фигуры.
4. Написать программу, которая по введенной длине отрезка и номеру единицы измерения (1 — дециметр, 2 — километр, 3 —метр, 4 — миллиметр, 5 — сантиметр) выводит соответствующее значение длины отрезка в метрах.
5. Написать программу, которая по введенному числу и номеру месяца выводит информацию, является ли этот день праздничным и название праздника.
6. Составить программу случайного выбора места летнего отдыха из семи предлагаемых туристическим агентством курортов, причем с вероятностью 3/10 придется отдыхать на даче.
7. Даны два вещественных положительных числа х и у. Арифметические действия над числами пронумерованы (сложение — 1, вычитание — 2, умножение — 3, деление — 4). Составить программу, которая по введенному номеру выполняет то или иное действие над числами.
8. Написать программу, которая по введенной массе и номеру единицы измерения (миллиграмм — 1, грамм — 2, килаграмм — 3, центнер — 4, тонна —5) выводит соответствующее значение массы в килограммах.
9. Пусть элементами треугольника являются: сторона а (первый элемент), площадь S (второй элемент), высота h (третий элемент), радиус вписанной окружности r (четвертый элемент), радиус описанной окружности R (пятый элемент). Составить программу, которая по введенному номеру и значению соответствующего элемента вычисляет значения всех остальных элементов треугольника. (Углы треугольника считаются известными).
10. Составить программу случайного выбора дежурного из списка, в котором 4 девушки и 4 молодых человека, причем для девушек вероятность выбора в два раза ниже.
11. Пусть элементами параллелограмма являются: сторона а (первый элемент), площадь S (второй элемент), высота h (третий элемент), диагональ d (четвертый элемент). Составить программу, которая по введенному номеру и значению соответствующего элемента вычисляет значения всех остальных элементов треугольника. (Углы параллелограмма считаются известными).
12. Написать программу, которая запрашивает натуральной число (от 0 до 99) в десятичном представлении и выводит его название на естественном языке. Например: 7 семь, 52 пятьдесят два
13. Вычислить порядковый номер дня по заданному числу, месяцу и году.
14. Написать программу, которая по введенному числу и месяцу выдает в качестве результата расписание занятий в этот день (год считать текущим).
15. Пусть элементами круга являются радиус (первый элемент), диаметр (второй элемент) и длина окружности (третий элемент). Составить программу, которая по номеру элемента запрашивала бы его соответствующее значение и вычисляла бы площадь круга.
16. Составить программу случайного выбора трех дисциплин, по которым придется сдавать экзамены, из предлагаемых на выбор четырех (всего возможно 4 варианта выбора).
17. В старояпонском календаре был принят 12-летний цикл. Годы внутри цикла носили названия животных: крысы, коровы, тигра, зайца, дракона, змеи, лошади, овцы, обезьяны, курицы, собаки и свиньи. Написать программу, которая вводит номер некоторого года и печатает его название по старояпонскому календарю. (Справка: 1996 г. — год Крысы — начало очередного цикла).
18. Даны два числа в виде дробей A/B и C/D. Арифметические действия над числами пронумерованы (сложение — 1, вычитание — 2, умножение — 3, деление — 4). Составить программу, которая по введенному номеру выполняет то или иное действие над этими числами, результат выводится в виде дроби.
19. Даны два комплексных числа A+jB и C+jD. Арифметические действия над числами пронумерованы (сложение — 1, вычитание — 2, умножение — 3, деление — 4). Составить программу, которая по введенному номеру выполняет то или иное действие над этими числами.
20. Написать программу расчета площади фигуры по названию (шар, конус, усеченный конус, куб, параллелепипед и цилиндр). Для вычисления площади, программа должна производить запрос необходимых параметров исходя из выбранной фигуры.
21. Написать программу, которая определяет принадлежит ли точка c координатами (x,y) фигуре, выбранной по соответствующему номеру (прямая — 1, парабола — 2, гипербола — 3, окружность — 4). Для вычисления принадлежности программа должна производить запрос необходимых параметров исходя из выбранной фигуры.
22. Составить программу, которая бы реализовала следующий алгоритм: по введенным названиям двух нот (до, ре, ми, фа, соль, ля, си) определить интервал, образованный нотами. Секунда - это интервал из двух соседних нот (по кругу), терция - интервал через ноту и т.д. (кварта, квинта, секста, септима).
23. Написать программу, которая по числу и номеру месяца рождения выдавала знак зодиака.
24. Написать программу, которая по введенным коэффициентам передаточной функции 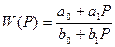 , определяла название простого звена.
, определяла название простого звена.
25. По введенному четырехзначному номеру аудитории вывести словами номер и адрес корпуса, где находится аудитория и на каком этаже. Пример: 3203 находится в третьем корпусе, распложенным по адресу Макаренко, 40 на втором этаже.
26. Составить программу перевода числа из одной системы счисления в другую. Для этого вначале должен быть предусмотрен выбор системы счисления вводимого числа, а затем выбор системы счисления, в которую осуществляется перевод. Примечание: для ввода и перевода чисел в различные системы счисления использовать манипуляторы потокового ввода и вывода.
27. По введенному четырехзначному номеру телефона вывести примерное расположение адреса абонента. Пример: 330245 – Падунский район, п.Энергетик, 5 микрарайон.
Лабораторная работа №3
Операторы прерывания цикла
В некоторых случаях желательно прервать повторение цикла, проанализировав какие-то условия внутри него. Это может потребоваться в тех случаях, когда проверки условия окончания цикла громоздкие, требуют многоэтапного сравнения и сопоставления каких-то данных и все эти проверки просто невозможно разместить в выражении условия операторов for, do…while или while.
Один из возможных вариантов решения этой задачи – использование оператора break. Оператор break прерывает выполнение тела любого цикла for, do или while и передает управление следующему за циклом выполняемому оператору.
Например, пусть в цикле осуществляется ввод с клавиатуры, который будет продолжаться до тех пор, пока пользователь не введет нужные значения:
#include<iostream.h>
main()
{
double A,B;
while(1){
cout <<"Введите значения больше нуля:"<<endl;
cout <<"A=";
cin >>A;
cout <<"B=";
cin >>B;
if ((A<=0)||(B<=0)) cout <<"Неправильные значения"<<endl;
else break; // Прерывание цикла
}
}
Еще один способ прерывания цикла – использование оператора goto, передающего управление какому-то оператору, расположенному вне тела цикла.
Описанные способы прерывали выполнение цикла. Имеется еще процедура continue, которая прерывает только выполнение текущей итерации, текущего выполнения тела цикла и передает управление на следующую итерацию.
Чтобы продемонстрировать применение continue, рассмотрим пример нахождения произведения 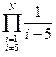 , которое можно организовать следующим образом:
, которое можно организовать следующим образом:
#include<iostream.h>
main()
{
int N;
cout <<"N=";
cin >> N;
double P=1;
for (int i=1; i<N; i++)
if (i==5) continue; // Прерывание текущей итерации цикла
else P*=1/double(i-5);
cout <<"P="<<P;
}
В этом варианте при i равном 5 текущая итерация прерывается и произведение не вычисляется, но цикл не прекращается.
Примеры, реализующие алгоритмы разветвляющейся структуры
Пример 1. Дана числовая последовательность и некоторое число e. Найти наименьший номер члена последовательности, для которого выполняется условие 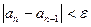 . Вывести на экран этот номер и все элементы
. Вывести на экран этот номер и все элементы 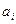 , где i =1,2,…, n.
, где i =1,2,…, n. 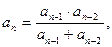
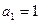 ,
, 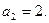 (при организации циклического повторения, следует использовать оператор цикла с постусловием do … while).
(при организации циклического повторения, следует использовать оператор цикла с постусловием do … while).
#include<iostream.h>
#include<math.h>
main()
{
double e;
cout <<"Введите e=";
cin >>e;
double a_n;
double a_n_1=2;
double a_n_2=1;
cout <<"a1="<<a_n_2<<endl;
cout <<"a2="<<a_n_1<<endl;
int i=2;
do { a_n=(a_n_1-a_n_2)/(a_n_1*a_n_2);
if(fabs(a_n-a_n_1)<e) { cout <<"a"<<i++<<"="<<a_n<<endl;
a_n_2=a_n_1;
a_n_1=a_n;
}
else break;l
} while (1);
cout<<"Последний номер последовательности"<<i;
}
Пример 2. Вычислить значения определенного интеграла 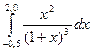 методом Симпсона с заданной точностью
методом Симпсона с заданной точностью 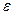 . (при организации циклического повторения, следует использовать оператор цикла с предусловием while).
. (при организации циклического повторения, следует использовать оператор цикла с предусловием while).
#include<iostream.h>
#include<math.h>
main()
{
const double a=-0.5;
const double b=2;
double e;
cout <<"Введите заданную точность=";
cin >>e;
int n;
cout <<"Введите начальное количество отрезков интегрирования=";
cin >>n;
double In=0,I2n=0;
double h,x;
int i;
while (!In||!I2n||fabs(I2n-In)/15>e)
{In=I2n;
h=(b-a)/(2*n);
I2n=a*a/((1+a)*(1+a)*(1+a));
I2n+=b*b/((1+b)*(1+b)*(1+b));
i=1;
while(i<=n) { x=a+h*(2*i-1);
I2n+=4*x*x/((1+x)*(1+x)*(1+x));
i++;
}
i=2;
while(i<=n) { x=a+h*(2*i-2);
I2n+=2*x*x/((1+x)*(1+x)*(1+x));
i++;
}
I2n=I2n*h/3;
n=n*2;
}
cout <<"Значение интеграла="<<I2n;
}
Пример 3. Дано натуральное число N. Выдать все пары “близнецов”, меньших N. “Близнецами” называют простые числа, разность между которыми равна 2. (при организации циклического повторения, следует использовать оператор цикла for):
#include<iostream.h>
main()
{
int N;
cout <<"Введите N=";
cin >>N;
int j,k;
for (int i=2; i<N-2; i++)
{for (j=2;i%j;j++);
for (k=2;(i+2)%k;k++);
if((j==i)&&(k==i+2))cout<<"("<<i<<";"<<i+2<<")-близнецы"
<< endl;
}
}
Варианты заданий
ЗАДАНИЕ I (для всех вариантов задания, при организации циклического повторения, следует использовать оператор цикла с постусловием do … while):
1 – 14. Дан числовой ряд и некоторое число e. Найти сумму тех членов ряда (n =1,2,3…), модуль которых больше или равен заданному числу e и вывести на экран все элементы числового ряда, которые входят в сумму. Общий член ряда имеет вид:
1. 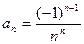 ;
2. ;
2. 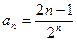 ;
3. ;
3. 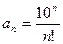 ;
4. ;
4. 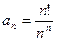 ;
5. ;
5. 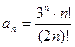 ;
6. ;
6. 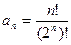 ;
7. ;
7. 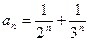 ; ;
| 8. 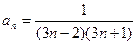 ;
9. ;
9. 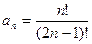 ;
10. ;
10. 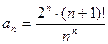 ;
11. ;
11. 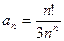 ;
12. ;
12. 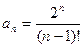 ;
13. ;
13. 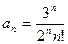 ;
14. ;
14. 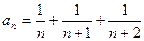 ; ;
|
15 – 28. Дана числовая последовательность и некоторое число e. Найти наименьший номер члена последовательности, для которого выполняется условие 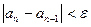 . Вывести на экран этот номер и все элементы
. Вывести на экран этот номер и все элементы 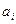 , где i =1,2,…, n.
, где i =1,2,…, n.
15. 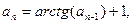 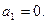 16.
16. 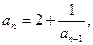 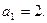 17.
17.  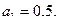 18.
18. 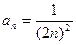 .
19. .
19. 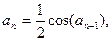 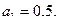 20.
20. 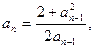 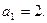 21.
21. 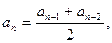
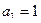 , , 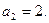
| 22. 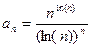 .
23. .
23. 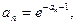 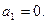 24.
24. 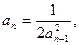 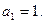 25.
25. 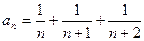 .
26. .
26. 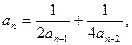
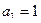 , , 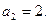 27.
27. 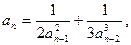
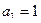 , , 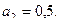 28.
28. 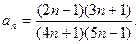
|
29 – 32. Дана числовая последовательность и некоторое число e. Найти наименьший номер элемента последовательности, для которого выполняется условие M. Вывести на экран номер и все элементы 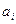 , где i =1,2,…, n.
, где i =1,2,…, n.
29. 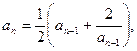 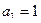 , ,
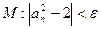 .
30. .
30. 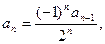 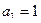 , ,
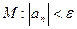 . .
| 31. 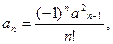 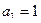 , ,
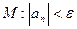 .
32. .
32. 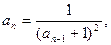 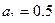 , ,
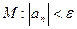 .
33. .
33. 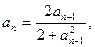 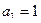 , ,
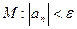
|
34 – 41. Составить программу для вычисления значений функции F ( x ) на отрезке [a , b] с шагом h. Результат представить в виде таблицы, первый столбец которой – значения аргумента, второй – соответствующие значения функции.
34. 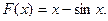 35.
35. 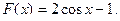 36.
36. 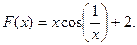 37.
37. 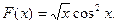
| 38. 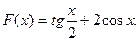 39.
39. 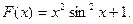 40.
40. 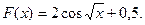 41.
41. 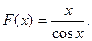
|
42 – 46. Дано натуральное число N . Вычислить
42. 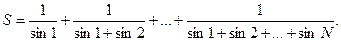
43. 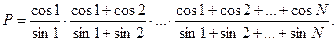
44. 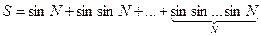 .
.
45. 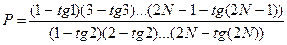 .
.
46 – 50. Даны натуральные числа n и k. Вычислить
46. 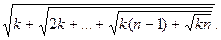
47. 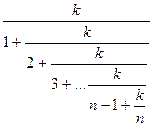 .
.
48. 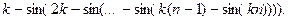
49. 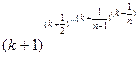 .
.
50. 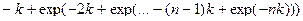 .
.
ЗАДАНИЕ II :
Вычислить значения определенных интегралов 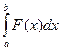 методом прямоугольников, методом трапеций и методом Симпсона с заданной точностью
методом прямоугольников, методом трапеций и методом Симпсона с заданной точностью 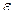 . Вычисления организовать в одном цикле таким образом, что при достижении требуемой точности вычисления интеграла одним методом, продолжать вычисления интеграла другими методами. (Для всех вариантов задания, при организации циклического повторения, следует использовать оператор цикла с предусловием while):
. Вычисления организовать в одном цикле таким образом, что при достижении требуемой точности вычисления интеграла одним методом, продолжать вычисления интеграла другими методами. (Для всех вариантов задания, при организации циклического повторения, следует использовать оператор цикла с предусловием while):
1. 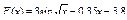 .
2. .
2. 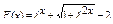 .
3. .
3. 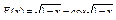 .
4. .
4. 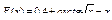 .
5. .
5. 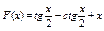 .
6. .
6. 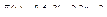 .
7. .
7. 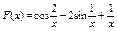 .
8. .
8. 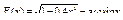 .
9. .
9. 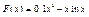 .
10. .
10. 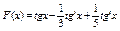 .
11. .
11. 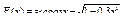 .
12. .
12. 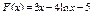 .
13. .
13. 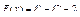 .
14. .
14. 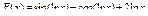 .
15. .
15.  .
16. .
16. 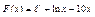 .
17. .
17. 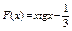 .
18. .
18. 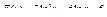 .
19. .
19. 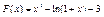 .
20. .
20. 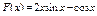 .
21. .
21. 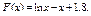 22.
22. 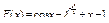 .
23. .
23. 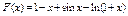 .
24. .
24. 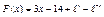 .
25. .
25.  . .
| 26. 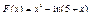 .
27. .
27. 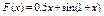 .
28. .
28. 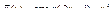 .
29. .
29. 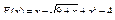 .
30. .
30. 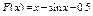 .
31. .
31. 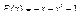 .
32. .
32. 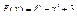 .
33. .
33. 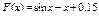 .
34. .
34. 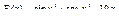 .
35. .
35. 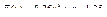 .
36. .
36. 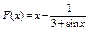 37.
37. 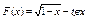 .
38. .
38. 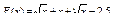 .
39. .
39. 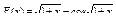 .
40. .
40. 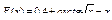 .
41. .
41. 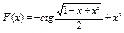 .
42. .
42. 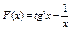 .
43. .
43. 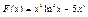 .
44. .
44. 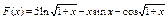 .
45. .
45. 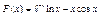 .
46. .
46. 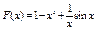 .
47. .
47. 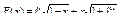 .
48. .
48. 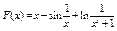 .
49. .
49. 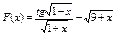 .
50. .
50. 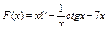 . .
|
ЗАДАНИЕ III (для всех вариантов задания, при организации циклического повторения, следует использовать оператор цикла for):
1. Определить существует ли двузначное число, которое равно квадрату числа его единиц, сложенному с кубом числа его десятков.
2. Определить, существует ли такая четверка последовательных натуральных чисел, сумма квадратов которых равна сумме квадратов трех следующих натуральных чисел.
3. Определить, является ли заданное число совершенным, т.е. равным сумме всех своих (положительных) делителей, кроме самого этого числа (например, число 6 совершенно: 6=1+2+3).
4. Найти все двузначные числа, удвоенная сумма цифр которых равна их произведению? (Пример: 36, 44, 63).
5. Найти все двузначные числа, равные утроенному произведению своих цифр. (Пример: 15, 24).
6. Найти все двузначные числа, которые обладают следующим свойством: куб суммы цифр числа равен квадрату самого числа. (Пример: 27).
7. Найти все трехзначные числа, представимые в виде сумм факториалов своих цифр. (Пример: 145).
8. Найти все трехзначные числа, которые можно представить разностью между квадратом числа, образованного первыми двумя цифрами и квадратом третьей цифры. (Пример: 100).
9. Найти все двузначные числа, сумма цифр которых не меняется при умножении числа на 2,3,4,5,6,7,8,9.
10. Можно ли заданное натуральное число М представить в виде суммы квадратов двух натуральных чисел? Написать программу решения этой задачи.
11. Привести дробь вида 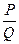 к несократимому виду.
к несократимому виду.
12. Дано натуральное число N. Найти и вывести все числа в интервале от 1 до N -1, у которых сумма всех цифр совпадает с суммой цифр данного числа. (Пример: N=44 – 17, 26, 35).
13. Дано натуральное число N. Найти наибольшее число M (M>1), на которое сумма цифр в цифровой записи числа N делится без остатка. (Пример: N=12345, сумма=15, M=5).
14. Найти все целые корни уравнения 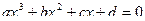 , где a , b , c и d – заданные целые числа, причем
, где a , b , c и d – заданные целые числа, причем 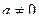 и
и 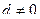 . Примечание: целыми корнями могут быть только положительные и отрицательные делители коэффициента d.
. Примечание: целыми корнями могут быть только положительные и отрицательные делители коэффициента d.
15. Натуральные числа a , b , c называются числами Пифагора, если выполняется условие 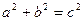 . Напечатать все числа Пифагора меньше заданного.
. Напечатать все числа Пифагора меньше заданного.
16. Долгожитель (возраст менее 100 лет) обнаружил однажды, что если к сумме квадратов цифр его возраста прибавить число дня его рождения, то как раз получится его возраст. Сколько лет долгожителю.
17. Найти наименьшее натуральное число n, представимое двумя различными способами в виде суммы кубов двух натуральных чисел.
18. Найти все натуральные числа, не превосходящие n, квадрат суммы цифр которых равен самому числу.
19. Найти все n – значные числа, сумма квадратов цифр которых кратна M.
20. Найти все натуральные числа, не превосходящие n, которые делятся на каждую из своих цифр без остатка.
21. Проверить, существует ли четырехзначное натуральное число, сумма пятых степеней цифр которого равна самому числу.
22. Проверить, существует ли четырёхзначное целое число, равное четвертой степени суммы своих цифр.
23. Определить пары натуральных чисел а < 100 и b < 100, произведение которых в 10 раз больше их суммы. Сколько таких пар?
24. Найдите все двузначные натуральные числа, которые равны утроенной сумме своих цифр.
25. Найдите все трехзначные натуральные числа, равные сумме кубов своих цифр.
26. Христиан Гольдбах, выдвинул так называемую проблему Гольдбаха, которая предполагает, что всякое целое число, большее или равное 6, может быть представлено в виде суммы трех простых чисел. Проверьте утверждение Гольдбаха для чисел, не превышающих число 100.
27. Христиан Гольдбах выдвинул гипотезу о том, что любое четное число, большее 2, представимо в виде суммы двух простых чисел. Проверьте эту гипотезу Гольдбаха для вcex четных чисел, не превышающих число 100.
28. Определить количество делителей у каждого из натуральных чисел от 1 до n.
29. Найти натуральное трехзначное число, у которого количество делителей максимально. Если таких чисел несколько, то должно быть выбрано максимальное из них. Вывести это число, а также все делители этого числа.
30. Найти все трехзначные простые числа (простым называется натуральное число, большее 1 и не имеющее других делителей, кроме единицы и самого себя).
31. Найти все целые числа из промежутка от 300 до 600, у которых сумма делителей кратна 10.
32. Три натуральных числа образуют дружественную тройку, если сумма собственных делителей каждого числа равна сумме двух других чисел. Отыскать дружественные тройки натуральных чисел.
33. Два натуральных числа называются "дружественными", если каждое из них равно сумме всех делителей другого, за исключением его самого (таковы, например, числа 220 и 284). Напечатать все пары "дружественных" чисел, не превосходящих заданного натурального числа.
34. Решить задачу Ферма. Найти куб, который в сумме со всеми его собственными делителями дает квадрат.
35. Составить программу нахождения цифрового корня натурального числа. Цифровой корень числа получается следующим образом. Складываем все цифры этого числа, затем все цифры найденной суммы и т. д., пока в результате не будет получено однозначное число (цифра), которое и называется цифровым корнем данного числа.
36. Найти все простые несократимые дроби, заключенные между 0 и 1, знаменатели которых не превышают 7 (дробь задается двумя натуральными числами — числителем и знаменателем).
37. Проверить, действительно ли при четном n число 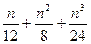 - целое.
- целое.
38. Составить программу, которая находит наибольшее значение отношения трехзначного числа к сумме его цифр.
39. Найти натуральное двухзначное число, у которого количество простых делителей максимально. Если таких чисел несколько, то должно быть выбрано минимальное из них. Вывести это число, а также все простые делители этого числа.
40. Найти натуральные числа, не превосходящие заданного, у которых делители являются только простыми числами. Вывести эти числа, а также их делители.
41. Дано натуральное число n. Получить все натуральные числа, меньшие n и взаимно простые с ним (два натуральных числа называются взаимно простыми, если их наибольший общий делитель равен 1).
42. Натуральное число из n цифр называется числом Армстронга, если сумма его цифр, возведенная в степень n, равна самому числу. Подсчитать все числа Армстронга из двух и трех цифр.
43. Найти двухзначное число а b, чтобы выполнялось уравнение 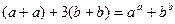 .
.
44. Определите количество наборов четырех различных нечетных натуральных чисел, сумма которых равна числу 50. Вывести наборы этих чисел.
45. Найти все трехзначные числа abc, у которых делителем является наименьшее общее кратное чисел a, b, c.
46. Найти все четырехзначные числа abc d, у которых делителем является наибольший общий делитель двухзначных чисел ab и c d .
47. Найти двухзначные числа, которые раскладываются на неповторяющиеся простые множители.
48. Дано натуральное число N. Найти и вывести все числа в интервале от 1 до N -1, у которых произведение всех цифр совпадает с суммой цифр данного числа. (Пример: N=44 – 18, 24).
49. Дано натуральное число N. Среди чисел 1... N такие, запись которых совпадает с последними цифрами записи их квадратов. (Пример: 62=36, 252=25).
50. Найти двухзначные числа, которые при возведении в квадрат дают палиндромы. Палиндром – это сочетание символов, которые читаются одинаково в прямом и обратном направлениях. (Пример: 262=676).
Лабораторная работа №4
Статическими массивами
Цель работы: закрепить практические навыки работы с системой программирования языка С++ на примере реализации алгоритмов над статическими массивами.
Основные теоретические сведения
Одномерные массивы
Массив представляет собой структуру данных, позволяющую хранить под одним именем совокупность данных любого, но только одного какого-то типа. Массив характеризуется своим именем, типом хранимых элементов и размерностью (количеством хранимых элементов).
Объявление переменной как одномерного массива имеет вид:
тип имя_массива [размерность]
В качестве размерности в объявлении массива разрешено использовать только константные выражения, ввиду чего такой массив будет являться статическим. Тип массива может быть любым.
Например,
int A [10];
объявляет массив с именем А, содержащий 10 целых чисел.
Доступ к элементам массива осуществляется выражением
имя_массива [номер_элемента]
где номер_элемента – индекс, являющийся целочисленным значением в диапазоне от 0 до размерность – 1. То есть номер первого элемента равен 0, а номер последнего элемента на 1 меньше размерности массива. Для предыдущего примера, А[0] - значение первого элемента, А[1] - второго, А[9] - последнего.
Работа с массивами, как правило, непосредственно связана с использованием операторов цикла.
Ниже приведен пример заполнения массива числами Фибоначчи, первые 2 из которых равны 1, а каждое последующее равно сумме двух предыдущих.
#include<iostream.h>
main()
{
int B[20];
B[0]=1;
B[1]=1;
for (int i=2; i<20; i++)
B[i]=B[i-1]+B[i-2];
for (i=0; i<20; i++)
cout <<"B["<<i<<"]="<<B[i]<<endl;
}
При объявлении массива значения элементов носят случайный характер, поэтому иногда желательно совместить объявление массива с заданием элементам начальных значений, т.е. инициализацией. Эти значения перечисляются в списке инициализации после знака равенства, разделяются запятыми и заключаются в фигурные скобки. Например:
int A[10] ={1,2,3,4,5,6,7,8,9,10};
double S[5] ={0.1,2.0,-3.2,0,6.5};
Таким образом, после данных объявлений A[2] будет содержать значение 3, а S[3] значение 0.
Если начальных значений меньше, чем элементов в массиве, оставшиеся элементы автоматически получают нулевые начальные значения. Например, оператор
int A[10] ={1,2,3};
задает значения первым трем элементам, а остальные будут равны 0. Оператор
int A[10] ={0};
присваивает нулевые значения всем элементам массива.
В объявлении массива со списком инициализации размерность массива можно не указывать. Тогда количество элементов массива будет равно количеству элементов в списке начальных значений. Например, объявление
double S[] ={0.1,2.0,-3.2,0,6.5};
создает массив из пяти элементов.
В объявлении массива в качестве размерности лучше всегда использовать именованные константы. Ниже приведен пример объявление массива, заполнение его случайными значениями от -10 до 10 и подсчет суммы его элементов:
#include<iostream.h>
#include<stdlib.h>
main()
{
randomize();
double c[15];
for (int i=0; i<15; i++)
c[i]=10-double(random(201))/10;
for (int i=0; i<15; i++)
cout <<"c["<<i<<"]="<<c[i]<<endl;
double S=0;
for (int i=0; i<15; i++) S+=c[i];
cout<<"S="<<S;
}
Если в дальнейшем потребуется массив не из 15 элементов, а, например, из 100, нужно будет изменить размерность массива и в объявлении, и во всех операторах, работающих с этим массивом (в данном случае в операторах for. Таких операторов в разных программах может быть очень много и поэтому она плохо масштабируется. Грамотнее будет реализовать этот пример следующим образом:
#include<iostream.h>
#include<stdlib.h>
main()
{
const int N=15; // объявление константы
randomize();
double c[N];
for (int i=0; i<N; i++)
c[i]=10-double(random(201))/10;
for (int i=0; i<N; i++)
cout <<"c["<<i<<"]="<<c[i]<<endl;
double S=0;
for (int i=0; i<N; i++) S+=c[i];
cout<<"S="<<S;
}
В этом случае мы вводим именованную константу N и используем ее во всех операторах, в которых требуется указать размерность массива. Тогда при необходимости изменения размерности массива, достаточно будет изменить его только в объявлении константы N.
const int N=100;
Программа сразу становится масштабируемой. А объявление N как константы гарантирует, что объявленное значение не будет случайно изменено где-то в программе.
Аналогичный результат можно получить, если заменить объявление константы директивой компилятора #define
#define N 10
В ряде случаев требуются константные массивы, данные из которых программа может только читать. Такие массивы обязательно должны инициализироваться в момент объявления. Например, требуется неизменяемый массив простых чисел, значения которых не больше 30:
const prime[] = {2,3,5,7,11,13,17,19,23,29};
Двумерные массивы
По аналогии с одномерными массивами, можно объявлять и многомерные статические массивы, т.е. массивы, элементами которых являются массивы. Например, двумерный массив можно объявить следующим образом:
int A2 [10] [3];
Такое объявление описывает двумерный массив, который можно представить себе как матрицу, состоящую из 10 строк и 3 столбцов.
Доступ к значениям элементов многомерного массива обеспечивается через номера элементов, заключенные в квадратные скобки. Например, А2[3][2] – значение элемента, лежащего на пересечении четвертой строки и третьего столбца. Также как и при работе с одномерными массивами номера элементов начинаются с 0.
Если многомерный массив инициализируется при его объявлении, список значений по каждой размерности заключается в фигурные скобки. Приведенный ниже оператор объявляет двумерный массив С размерностью 4 на 3 и инициализируется.
int C[4][3]= {{1,2,3},{4,5,6},{7,8,9},{10,11,12}};
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
| 10 | 11 | 12 |
В этом случае, элемент С[1][2] равен 6, а элемент С[2][1] равен 8 и т.д.
Если в списке инициализации в какой-то из размерностей не хватает данных, то все дальнейшие не перечисленные элементы считаются равными нулям. Например
double D [5] [4] = {{1.0,2.1,3.2,1.8},
{-4.1,5.0,1.1},
{-7.1,2.2}};
создаст матрицу размерностью 5 на 4, состоящую из элементов вещественных чисел и присвоит им следующие начальные значения:
| 1.0 | 2.1 | 3.2 | 1.8 |
| -4.1 | 5.0 | 1.1 | 0 |
| -7.1 | 2.2 | 0 | 0 |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 |
Работа с двумерными массивами непосредственно связана с использованием одновременно двух операторов цикла, внешнего и внутреннего. Например, необходимо определить в двумерном случайно заполненном массиве, каких чисел больше положительных или отрицательных. Ноль во внимание не принимается:
#include<iostream.h>
#include<stdlib.h>
main()
{
const int n=5;
const int m=10;
randomize();
int matr[n][m];
int i,j;
for (i=0; i<n; i++)
for (j=0; j<m; i++) matr[i][j]=100-random(201);
for (i=0; i<n; i++) {
for (j=0; j<m; i++) cout <<matr[i][j]<<" ";
cout <<endl;
}
int p=0;
for (i=0; i<n; i++)
for (j=0; j<m; i++)
if (matr[i][j]!=0)
if (matr[i][j]>0) p++;
else p--;
if (p==0) cout <<"равное количество";
else if (p>0) cout <<"положительных больше";
else cout <<"отрицательных больше";
}
Сортировка массивов
Задачей сортировки массивов является преобразование исходной последовательности элементов массива в последовательность, содержащую те же элементы, но в порядке возрастания (или убывания) значений.
Сортировка методом выбора. При сортировке массива a[0], a[1], ..., a[N-1] методом простого выбора среди всех элементов находят элемент с наибольшим значением a[i], и этот элемент ставят в самый конец массива, т.е. поменять местами значения элементов массива a[ i ] и a[ N -1]. Далее, игнорируя последний элемент массива a[ N-1], следует выполнить поиск наибольшего элемента в подмассиве a[0], a[1], ..., a[ N -2] и поменять его местами с последним элементом подмассива a[ N -2]. Этот процесс повторяется до тех пор, пока не будут найдены N -1 наибольших значений и не дойдем до подмассива a[0], содержащего к этому моменту наименьшее значение. Работа алгоритма иллюстрируется следующим примером:
| Исходная последовательность N =7: | ||||||
| 3 | 1 | 7 | 5 | 6 | 4 | 2 |
| max =7 из a[0]…a[N-1] | ||||||
| 3 | 1 | 2 | 5 | 6 | 4 | 7 |
| max =6 из a[0]…a[N-2] | ||||||
| 3 | 1 | 2 | 5 | 4 | 6 | 7 |
| max =5 из a[0]…a[N-3] | ||||||
| 3 | 1 | 2 | 4 | 5 | 6 | 7 |
| max =4 из a[0]…a[N-4] | ||||||
| 3 | 1 | 2 | 4 | 5 | 6 | 7 |
| max =3 из a[0]…a[N-5] | ||||||
| 2 | 1 | 3 | 4 | 5 | 6 | 7 |
| max =2 из a[0]…a[1] | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Программная реализация этого метода на языке Си++, будет выглядеть следующей:
#include<iostream.h>
#include<stdlib.h>
main()
{
const N=7; //размерность массива
int A[N];
randomize();
int i;
for(i=0; i<N; i++) A[i]=random(10);//заполнение массива
int index, max,j;
for (i=N-1; i>0; i--)
{ max=A[0];
index=0;
for(j=1; j<=i; j++)
if (A[j]>max) { index=j;
max=A[j];
}
A[index]=A[i];
A[i]=max;
}
}
Если в условии if(A [ j ]> max), поменять знак операции сравнения на меньше (<), то будут выбираться наименьшие значения и сортировка массива будет осуществляться по убыванию.
Сортировка методом обмена. При сортировке массива a[0], a[1], ..., a[ N -1] методом обмена (“методом пузырька”), начиная с первого элемента сравнивают два соседних элемента (a[ i ] и a[ i +1]) и меняют их местами, если a[ i ]>a[ i +1], т.е. если они нарушают порядок. Такое сравнение и обмен выполняют до тех пор, пока не будет достигнут конец массива и последним элементом a [ N -1] окажется элемент массива с наибольшим значением. Далее, игнорируя последний элемент массива a[ N -1], следует повторить такую же схему сравнения и обмена в подмассиве a[0], a[1], ..., a[ N -2]. И так далее. На последнем шаге будут сравниваться только текущие значения a[0] и a[1]. Работа алгоритма иллюстрируется следующим примером:
| Исходная последовательность N =5: | 6 | 3 | 7 | 1 | 5 |
| Шаг 1: | 6 | 3 | 7 | 1 | 5 |
| 3 | 6 | 7 | 1 | 5 | |
| 3 | 6 | 7 | 1 | 5 | |
| 3 | 6 | 1 | 7 | 5 | |
| 3 | 6 | 1 | 5 | 7 | |
| Шаг 2: | 3 | 6 | 1 | 5 | 7 |
| 3 | 6 | 1 | 5 | 7 | |
| 3 | 1 | 6 | 5 | 7 | |
| 3 | 1 | 5 | 6 | 7 | |
| Шаг 3: | 3 | 1 | 5 | 6 | 7 |
| 1 | 3 | 5 | 6 | 7 | |
| 1 | 3 | 5 | 6 | 7 | |
| Шаг 4: | 1 | 3 | 5 | 6 | 7 |
| 1 | 3 | 5 | 6 | 7 | |
| Итоговая последовательность: | 1 | 3 | 5 | 6 | 7 |
Программная реализация этого метода на языке Си, будет выглядеть следующей:
#include<iostream.h>
#include<stdlib.h>
main()
{
const N=7;
int A[N];
randomize();
int i;
for (i=0; i<N; i++) A[i]=random(100);
int swap, j;
for (i=N-1; i>1; i--)
for(j=0; j<i; j++)
if (A[j]>A[j+1]) {swap=A[j+1];
A[j+1]=A[j];
A[j]=swap;
}
}
Если в условии if (A[j]>A[j+1]), поменять знак операции сравнения на меньше (<), то последними элементами в подмассивах будут оказываться наименьшие значения и сортировка массива будет осуществляться по убыванию.
Сортировка челночным методом. При сортировке массива a[0], a[1], ..., a[ N -1] челночным методом, начиная с первого элемента сравнивают два соседних элемента (a[ i ] и a[ i +1]), если порядок нарушен (a[ i ]<=a[ i +1]), то продвигаются на один элемент вперед (i = i +1), если порядок нарушен (a[ i ]>a[ i +1]), то производится перестановка и сдвигаются на один элемент назад ( i = i -1). Таким образом сравнивая и переставляя элементы доходят до конца массива ( i = N -1), при этом массив становится упорядоченным. Работа алгоритма иллюстрируется следующим примером:
| Исходная последовательность N =5 | 3 | 1 | 7 | 5 | 2 |
| i=0 (порядок нарушен) | 3 | 1 | 7 | 5 | 2 |
| i=0 (порядок не нарушен) | 1 | 3 | 7 | 5 | 2 |
| i=1 (порядок не нарушен) | 1 | 3 | 7 | 5 | 2 |
| i=2 (порядок нарушен) | 1 | 3 | 7 | 5 | 2 |
| i=1 (порядок не нарушен) | 1 | 3 | 5 | 7 | 2 |
| i=2 (порядок не нарушен) | 1 | 3 | 5 | 7 | 2 |
| i=3 (порядок нарушен) | 1 | 3 | 5 | 7 | 2 |
| i=2 (порядок нарушен) | 1 | 3 | 5 | 2 | 7 |
| i=1 (порядок нарушен) | 1 | 3 | 2 | 5 | 7 |
| i=0 (порядок не нарушен) | 1 | 2 | 3 | 5 | 7 |
| i=1 (порядок не нарушен) | 1 | 2 | 3 | 5 | 7 |
| i=2 (порядок не нарушен) | 1 | 2 | 3 | 5 | 7 |
| i=3 (порядок не нарушен) | 1 | 2 | 3 | 5 | 7 |
| i=4: Итоговая последовательность | 1 | 2 | 3 | 5 | 7 |
Программная реализация этого метода на языке Си++, будет выглядеть следующей:
#include<iostream.h>
#include<stdlib.h>
main()
{
const N=7;
int A[N];
randomize();
int i;
for (i=0; i<N; i++) A[i]=random(100);
int swap;
i=0;
while (i<N-1)
if (A[i]>A[i+1]) {swap=A[i+1];
A[i+1]=A[i];
A[i]=swap;
i--;
if (i<0) i=0;
}
else i++;
}
Если в условии if (A[ i ]>A[ i +1]), поменять знак операции сравнения на меньше (<), то сортировка массива будет осуществляться по убыванию.
Сортировка методом вставок. Данный метод сортировки массива основан на вставке элементов из неупорядоченной части массива в упорядоченную. Считается, что первоначально массив a[0], a[1], ..., a[ N -1] является не отсортированным, поэтому упорядоченная часть будет состоять из одного первого элемента a[0], а неупорядоченная из всех элементов массива a[1], ..., a[ N -1]. На каждом шаге метода из неупорядоченной части извлекается первый элемент и помещается в упорядоченную, так чтобы не нарушался порядок. При этом количество элементов в упорядоченной части увеличивается на 1, а в неупорядоченной уменьшается на 1. Процесс вставки элементов происходит до тех пор, пока весь массив не окажется отсортированным.
| Исходная последовательность N =7: | 3 | 1 | 7 | 5 | 6 | 4 | 2 | |
| 3 | 1 | 7 | 5 | 6 | 4 | 2 | ||
| 1 | 3 | 7 | 5 | 6 | 4 | 2 | ||
| 1 | 3 | 7 | 5 | 6 | 4 | 2 | ||
| 1 | 3 | 5 | 7 | 6 | 4 | 2 | ||
| 1 | 3 | 5 | 6 | 7 | 4 | 2 | ||
| 1 | 3 | 4 | 5 | 6 | 7 | 2 | ||
| Итоговая последовательность: | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
Программная реализация этого метода на языке Си, будет выглядеть следующей:
#include<iostream.h>
#include<stdlib.h>
main()
{
const N=7;
int A[N];
randomize();
int i,j,element;
for (i=0; i<N; i++) A[i]=random(100);
for (i=1; i<N; i++)
{ element=A[i];
j=i;
while (A[j-1]>element)
{A[j]=A[j-1];
j--;
if (j<1) break;
}
A[j]=element;
}
for (i=0; i<N; i++) cout << A[i]<< " ";
}
Если в условии while (A [ j -1]> element), поменять знак операции сравнения на меньше (<), то сортировка массива будет осуществляться по убыванию.
Примеры программ, реализующие алгоритмы работы со статическими массивами
Пример 1. Среди заданных N точек на плоскости найти две, что прямые, проходящие через них перпендикулярно соединяющему эти точки отрезку, образуют полосу, в которой содержится максимальное количество точек из множества N.
Рассмотрим для решения этой задачи необходимые сведения и формулы.
Уравнение прямой, проходящей через точки P, Q, имеет вид:
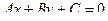 ,
,
где 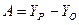 ,
, 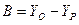 ,
,
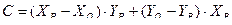 ;
;
Уравнение прямой, проходящей через точку P перпендикулярно отрезку PQ, имеет вид:
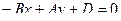 ,
,
где 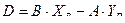 .
.
Если в уравнении прямой подставить координаты точек, лежащих по одну сторону от этой прямой, получим значения одного знака, иначе – разных знаков.
#include<iostream.h>
#include<stdlib.h>
#include<conio.h>
main()
{
clrscr();
const int N=20;
randomize();
double x[N];
double y[N];
int i;
for (i=0; i<N; i++)
{
x[i]=double(random(401)-200)/10;
y[i]=double(random(401)-200)/10;
}
for (i=0; i<N; i++)
cout <<i+1<<"-точка ("<<x[i]
<<";"<<y[i]<<");"<<endl;
double A,B,C;
double AP,BP,CP;
double AQ,BQ,CQ;
double Z1,Z2,Z3;
int max=0,tek,P,Q,N1,N2;
//выбираем очередную пару точек
for(P=0; P<N-1; P++)
for(Q=P+1; Q<N; Q++)
{
//находим коэффициенты уравнения прямой PQ
A=y[P]-y[Q];
B=x[Q]-x[P];
C=(x[P]-x[Q])*y[P]+(y[Q]-y[P])*x[P];
//прямые, проходящие через P, Q перпендикулярно PQ
AP=-B;
BP=A;
CP=B*x[P]-A*y[P];
AQ=-B;
BQ=A;
CQ=B*x[Q]-A*y[Q];
//определим, сколько точек попадает в полосу
tek=0;
Z1=AP*x[Q]+BP*y[Q]+CP;
Z3=AQ*x[P]+BQ*y[P]+CQ;
//просматриваем все точки, кроме P и Q
for(i=0; i<N; i++)
if (i!=Q && i!=P)
{
//точки i и Q должны быть по одну сторону от
//прямой, проходящей через P
Z2=AP*x[i]+BP*y[i]+CP;
if (Z1*Z2>0)
{
//точки i и P должны быть по одну сторону от
//прямой, проходящей через Q
Z2=AQ*x[i]+BQ*y[i]+CQ;
if (Z3*Z2>0) tek++;
}
}
if (tek>max)
{
max=tek;
N1=P;
N2=Q;
}
}
cout<<"Исходные точки:"<<endl
<<"("<<x[N1]<<";"<<y[N1]<<")"<<endl
<<"("<<x[N2]<<";"<<y[N2]<<")"<<endl;
getch();
}
Пример 2. Дано множество A из N пар точек с целочисленными координатами. Расположить точки данного множества по возрастанию значений пересечения прямой, проходящей через эту точку, с осью абсцисс. Пары точек, через которые проходит прямые параллельные прямые исключить из сортировки. Сортировку произвести методом обмена.
#include<iostream.h>
#include<conio.h>
#include<stdlib.h>
main()
{
const N=10;
int X1[N],Y1[N];
int X2[N],Y2[N];
int i;
randomize();
//заполнение массивов случайным образом
for (i=0;i<N;i++)
{
X1[i]=random(41)-20;
Y1[i]=random(41)-20;
X2[i]=random(41)-20;
Y2[i]=random(41)-20;
}
//вывод первоначальных данных
for (i=0;i<N;i++)
cout<<i+1<<" пара точек:"<<endl
<<"("<<X1[i]<<";"<<Y1[i]<<") "
<<"("<<X2[i]<<";"<<Y2[i]<<") "<<endl;
int R=N;
i=0;
int swapX1,swapX2,swapY1,swapY2;
//исключение пар точек, прямые через которые
//параллельны оси абсцисс, поместив их в конец
//массива
while (i<R && R>1)
if (Y1[i]==Y2[i]) {
swapX1=X1[R-1];
swapY1=Y1[R-1];
swapX2=X2[R-1];
swapY2=Y2[R-1];
X1[R-1]=X1[i];
Y1[R-1]=Y1[i];
X2[R-1]=X2[i];
Y2[R-1]=Y2[i];
X1[i]=swapX1;
Y1[i]=swapY1;
X2[i]=swapX2;
Y2[i]=swapY2;
R--;
}
else i++;
//сортировка R пар точек, прямые через которые
//пересекаю ось абсцисс
int j;
double A1,A2;
for (i=R-1; i>1; i--)
for(j=0; j<i; j++)
{
A1=(X1[j]-X2[j])*Y1[j]-(Y1[j]-Y2[j])*X1[j];
A1=A1/(Y1[j]-Y2[j]);
A2=(X1[j+1]-X2[j+1])*Y1[j+1]-(Y1[j+1]-
Y2[j+1])*X1[j+1];
A2=A2/(Y1[j+1]-Y2[j+1]);
if (A1>A2) { swapX1=X1[j+1];
swapY1=Y1[j+1];
swapX2=X2[j+1];
swapY2=Y2[j+1];
X1[j+1]=X1[j];
Y1[j+1]=Y1[j];
X2[j+1]=X2[j];
Y2[j+1]=Y2[j];
X1[j]=swapX1;
Y1[j]=swapY1;
X2[j]=swapX2;
Y2[j]=swapY2;
}
}
//Вывод исключенных пар точек
if (R!=N)
{
cout<<"Исключенные точки:"<<endl;
for (i=R;i<N;i++)
cout <<"("<<X1[i]<<";"<<Y1[i]<<") "
<<"("<<X2[i]<<";"<<Y2[i]<<") "<<endl;
}
//Вывод отсортированных пар точек
cout<<"Отсортированные пары точек:"<<endl;
for (i=0;i<R;i++)
cout <<"("<<X1[i]<<";"<<Y1[i]<<") "
<<"("<<X2[i]<<";"<<Y2[i]<<") "<<endl;
getch();
}
Варианты заданий
ЗАДАНИЕ I:
Для всех вариантов заполнение массива организовать в ходе выполнения программы вводом значений с клавиатуры. Также в вариантах, где задан упорядоченный по возрастанию массив, осуществить проверку правильности ввода значений.
1. Дан массив, заполненный целочисленными значениями. Найти количество его локальных минимумов и максимумов, а также определить из них максимальный и минимальный.
2. Дан массив, заполненный целочисленными значениями. Определить количество его промежутков монотонности (то есть участков, на которых его элементы возрастают или убывают).
3. Дан целочисленный массив размера N. Если он является перестановкой, то есть содержит все числа от 1 до N, то вывести 0, в противном случае вывести номер первого недопустимого элемента.
4. Дан целочисленный массив. Назовем серией группу подряд идущих одинаковых элементов, а длиной серии — количество этих элементов (длина серии может быть равна 1). Вывести массив, содержащий длины всех серий исходного массива.
5. Дано множество A из N точек с координатами ( x , y ). Среди всех точек этого множества найти точки наиболее близкие и наиболее удаленные от начала координат, лежащие в первой, второй, третьей и четвертой четверти.
6. Дано множество A из N точек с координатами ( x , y ). Найти пары различных точек этого множества с минимальным и максимальным расстоянием между ними и сами эти расстояния.
7. Дано множество A из N точек с координатами ( x , y ). Найти две точки из данного множества. Для одной точки сумма расстояний до остальных точек должна быть минимальна, а для другой максимальна.
8. Даны множества A и B, состоящие соответственно из N1 и N2 точек с координатами ( x , y ). Найти минимальное и максимальное расстояние между точками этих множеств и сами точки, расположенные на этом расстоянии.
9. Дано множество A из N точек с координатами ( x , y ). Найти наименьший периметр треугольника, вершины которого принадлежат различным точкам множества A, и сами эти точки (точки выводятся в том же порядке, в котором они перечислены при задании множества A).
10. Дано множество A из N точек с координатами ( x , y ). Найти три точки из этого множества, которые составляли бы вершины треугольника, и сумма расстояний от сторон до других точек была бы минимальна.
11. Дано множество A из N точек с координатами ( x , y ). Определить количество прямоугольных треугольников, которые создаются этими точками.
12. Дано множество A из N точек с координатами ( x , y ). Найти точку из этого множества, которая являлась бы центром окружности с минимальным радиусом. Все точки множества должны находится внутри этой окружности.
13. Дано множество A из N точек с координатами ( x , y ). Найти наибольшую длину ломанной линии, которую можно составить из точек этого множества.
14. Секретный замок для сейфа состоит из 10 расположенных в ряд ячеек, в которые надо вставить игральные кубики. Но дверь открывается только в том случае, когда в любых трех соседних ячейках сумма точек на передних гранях кубиков равна 10. (Игральный кубик имеет на каждой грани от 1 до 6 точек.) Напишите программу, которая разгадывает код замка при условии, что два кубика уже вставлены в ячейки.
15. В целочисленном массиве найти повторяющиеся числа. Вывести эти числа, а также количество их повторений.
16. Дано вещественное число x и целочисленный массив. В массиве найти два члена, расположенных в диапазоне между максимальным и минимальным значениями, среднее арифметическое которых ближе всего к x.
17. Даны две последовательности: a 1 , a 2 , ..., an и b 1 , b 2 , ..., bm (m < n). В каждой из них члены различны. Определить входят ли все члены второй последовательности в первую последовательность, а также вывести те значения первой последовательности, которые не представлены во второй.
18. Задан массив A размером N. Определить значения k (k ≠0 и k ≠ N -1), при котором выполняется соотношение:
|max(A[0]...A[k])-max(A[k+1]...A[N-1])|< |min(A[0]...A[k])-min(A[k+1]...A[N-1])|.
19. Дан массив целых чисел М1. Вводим массив М2, размер которого значительно меньше, чем у М2. Определить, сколько раз массив М2 встречается в М1.
20. Проверить, существует ли в заданном целочисленном массиве такой диапазон чисел, которые являются элементами арифметической или геометрической прогрессии. При существовании вывести первые и последние элементы этого диапазона.
21. Написать программу определения в одномерном массиве целых чисел наибольшего количества последовательно расположенных чисел, образующих «пилу». Например, пилу
образуют числа 3, 7, 5, 9, 2, 4, 1, 6.
22. Задан упорядоченный по возрастанию массив целых чисел. Написать программу, позволяющую вставить в этот массив вводимое с клавиатуры число без нарушения упорядоченности. Предполагается, что размер заданного массива не увеличивается. Поэтому требуется определить, вставлять ли в массив элемент, по величине больший (меньший) всех элементов массива. Это можно сделать, удалив наименьший (наибольший) по величине элемент. Затем нужно определиться с направлением сдвига элементов при освобождении места. Если исключить вариант вставки таких элементов и сдвигать в сторону большие по величине элементы, то останется только определить место вставки, сдвинуть элементы, освобождая место для вставки, и вставить вводимое число.
23. Образуем числовую последовательность. Начальный элемент — произвольное натуральное число, кратное трем; за любым элементом последовательности следует число, равное сумме кубов всех цифр данного элемента. Доказать, что такая последовательность, начиная с некоторого места, становится постоянной и равной некоторому числу. Чему равно это число? Примечание: Числовую последовательность реализовать в виде массива.
24. Первый член последовательности — четырехзначное целое число, цифры которого не все одинаковые. Каждый последующий элемент образуется следующим образом. Цифры предыдущего элемента располагаем в убывающем порядке (первое число) и в возрастающем порядке (второе число). Из первого числа вычитаем второе и получаем следующий элемент последовательности. Показать, что такая последовательность, начиная с некоторого элемента, становится постоянной и равной некоторому числу. Чему равно это число? Примечание: Числовую последовательность реализовать в виде массива.
25. В одномерном массиве с четным количеством элементов (2N) находятся координаты N точек плоскости. Они располагаются в следующем порядке: х1, у1, х2, у2, х3, у3 и т. д.
Определить номера точек, которые могут являться вершинами равнобедренного треугольника.
26. Задан целочисленный массив размерности N. Определить, есть ли среди элементов массива простые числа. Если да, то вывести номера этих элементов.
27. На плоскости n точек заданы своими координатами, а также дана окружность радиуса R с центром в начале координат. Указать множество всех треугольников с вершинами в заданных точках, пересекающихся с окружностью.
28. В одномерном массиве все отрицательные элементы переместить в начало массива, а остальные – в конец с сохранением порядка следования. Дополнительный массив заводить не разрешается.
29. В одномерном массиве с четным количеством элементов (2 N) находятся координаты N точек плоскости. Они располагаются в следующем порядке: х1, у1, х2, у2, х3, у3 и т. д. Определить номера точек, которые могут являться вершинами квадрата.
30. В одномерном массиве с четным количеством элементов (2 N) находятся координаты N точек плоскости. Они располагаются в следующем порядке: х1, у1, х2, у2, х3, у3 и т. д. Определить три точки, являющиеся вершинами треугольника, для которого разность точек вне его и внутри является минимальной.
31. Дано множество A из N точек с координатами ( x , y ). Найти такие пары точек этого множества, что проведенные через них линии параллельны осям координат.
32. Задан массив A размером N. Определить значения k (k ≠0 и k ≠ N -1), при котором соотношение |max ( A [0]... A [ k ])- max ( A [ k +1]... A [ N -1])| является минимальным.
33. Разделить массив на две части, поместив в первую элементы, большие среднего арифметического их суммы, а во вторую меньшие (сортировку не использовать)
34. Дан массив из N четырехзначных натуральных чисел. Определить и вывести на экран все группы чисел, у которых суммы первых двух цифр и суммы двух последних цифр равны.
35. Дано множество C комплексных чисел, состоящее из двух массивов вещественных чисел A и B размерностью N (c=a+jb). Найти минимальное и максимальное значения аргумента комплексного числа в диапазоне между максимальным и минимальным значениями модуля комплексного числа. Примечание: модуль комплексного числа определяется 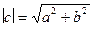 , а аргумент
, а аргумент 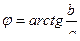 .
.
36. Дан массив неповторяющихся целых чисел. Найти наименьшее число элементов, которые нужно выкинуть из данной последовательности, чтобы осталась возрастающая последовательность.
37. На координатной плоскости дано множество парабол, которые описываются уравнениями 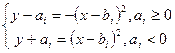 . Параметры парабол ai и bi заключены в вещественных массивах A и B размерностью N. Определить пары парабол, которые не пересекаются.
. Параметры парабол ai и bi заключены в вещественных массивах A и B размерностью N. Определить пары парабол, которые не пересекаются.
38. На координатной плоскости дано N точек с координатами ( x , y ). Найти такие пары точек этого множества, что проведенные через них прямые линии пересекают одновременно и окружность 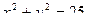 и квадратичную параболу
и квадратичную параболу  .
.
39. На координатной плоскости дано N точек с координатами ( x , y ), которые являются вершинами N – угольника. Найти площадь и периметр заданного N – угольника, а также определить является ли он правильным.
40. Дан массив из N натуральных целых чисел. Найти наименьшее общее кратное этих чисел.
41. Дан массив из N натуральных целых чисел. Определить последовательность простых чисел, которые встречаются среди множителей значений заданного массива хотя бы один раз. Примечание: Использовать дополнительный массив для хранения последовательности простых чисел не разрешается. (Пример: { 2, 6, 14, 37, 22}-> 2, 3, 7, 11, 37).
42. Дан массив из N натуральных целых чисел. Определить пару чисел, которые имеют наибольшее количество одинаковых делителей.
43. Дано множество A из N точек с координатами ( x , y ). Найти точку с минимальным суммарным отклонением от других точек заданного множества.
44. Дан массив из N натуральных целых чисел. Определить пары троек чисел с равными суммами. Примечание: Одно и тоже число не может входить одновременно в обе тройки.
45. Задан целочисленный массив A размером N. Определить при каком значении индекса k (k ≠0 и k ≠ N -1), заданный массив разбивается на две числовые последовательности с наиболее близкими средними арифметическими значениями.
46. Даны две последовательности вещественных чисел X и Y размерностью N 1 и N 2. Определить при каких значениях  и
и  функция
функция 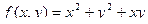 примет минимальное и максимальное значения.
примет минимальное и максимальное значения.
47. Даны две последовательности целых чисел X и Y размерностью N 1 и N 2. Определить такие значения i и j, при которых выражение 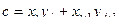 является наибольшей.
является наибольшей.
48. Даны два целочисленных массива разной размерностью. Считать, что среднее арифметическое значение первого массива больше, чем среднее арифметическое второго. За минимальное количество обменов элементами между массивами, преобразовать их так, чтобы среднее арифметическое первого массива стало меньше второго.
49. Дана целочисленная последовательность A размерностью N. Найти наименьшее число K элементов, которые можно выкинуть из данной последовательности, так чтобы осталась возрастающая последовательность.
50. Даны две последовательности целых чисел X и Y размерностью N. Определить такие значения i и j, при которых выражение 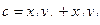 является наименьшей.
является наименьшей.
ЗАДАНИЕ II:
Для всех вариантов заполнение массива организовать с помощью датчика случайных чисел.
1 – 4. Дано множество С, состоящее из массивов вещественных чисел A и B размерностью N. Причем значения элементов массива B определяются следующим образом: B [0]=0, B [ i ]= A [ i ]- A [ i -1] i =1.. N -1. Считать, что значение множества С[ k ]≥ C [ m ], если либо A [ k ]≥ A [ m ] или A [ k ]< A [ m ] и A [ k ]+ B [ k ]≥ A [ m ]+B [ m ]. Отсортировать множество С по возрастанию в соответствии с указанным условием. Сортировку произвести:
1. методом обмена;
2. методом вставкой;
3. методом выбора;
4. методом Шелла.
5 – 8. Дано множество C комплексных чисел, состоящее из двух массивов вещественных чисел A и B размерностью N (c=a+jb). Отсортировать данное множество комплексных чисел по убыванию значений их модулей. Примечание: модуль комплексного числа равен 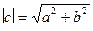 . Сортировку произвести:
. Сортировку произвести:
5. методом обмена;
6. методом вставкой;
7. методом выбора;
8. методом Шелла.
9 – 12. Целочисленный массив X из n элементов разбит на m фрагментов. В целочисленном массиве K из m элементов хранятся длины соответствующих фрагментов (все K [ i ] различны, их сумма равна n). Упорядочить массив K по возрастанию, переставив соотвествующие фрагменты в массиве X.
Сортировку произвести:
9. методом обмена;
10. методом вставкой;
11. методом выбора;
12. методом Шелла.
13 – 16. Дана некоторая функция f ( x , y ) и множество A из N точек с целочисленными координатами ( x , y ), состоящее из двух массивов. Известно, что значение функции f ( x , y ) в точке ( x 0 , y 0 ) равно площади фигуры, образованной прямыми y = x 0 и x = y 0 c осями координат. Расположить точки данного множества в соответствии с убыванием значений заданной функции.
Сортировку произвести:
13. методом обмена;
14. методом вставкой;
15. методом выбора;
16. методом Шелла.
17 – 20. Дано множество A из N точек с координатами ( x , y , z ). Расположить точки данного множества по увеличению расстояния от начала координат до соответствующей точки.
Сортировку произвести:
17. методом обмена;
18. методом вставкой;
19. методом выбора;
20. методом Шелла.
21 – 24. Дан целочисленный массив A из N точек. Расположить значения данного массива по убыванию в диапазоне между максимальным и минимальным значениями. Максимальное и минимальное значение не входят в диапазон сортировки.
Сортировку произвести:
21. методом обмена;
22. методом вставкой;
23. методом выбора;
24. челночным методом.
25 – 28. Дана некоторая функция f ( x , y ) и множество A из N точек с целочисленными координатами ( x , y ), состоящее из двух массивов. Известно, что значение функции f ( x , y ) в точке ( x 0 , y 0 ) равно площади фигуры, образованной осями координат и прямой, проходящей через точку ( x 0 , y 0 ) под углом 45 ° к осям в той четверти координат, где находится эта точка. Расположить точки данного множества в соответствии с увеличением значений заданной функции.
Сортировку произвести:
25. методом обмена;
26. методом вставкой;
27. методом выбора;
28. челночным методом.
29 – 32. Даны два целочисленных массива A и B из N точек. Отсортировать массив A по возрастанию, а массив B по убыванию и после этого поменять местами четные элементы массивов. Затем отсортировать массив A по убыванию, а массив B по возрастанию.
Сортировку массивов произвести:
29. методом обмена;
30. методом вставкой;
31. методом выбора;
32. челночным методом.
33 – 36. Дана некоторая функция f ( x , y ) и множество A из N точек с целочисленными координатами ( x , y ), состоящее из двух массивов. Известно, что значение функции f ( x , y ) в точке ( x 0 , y 0 ) равно площади фигуры, образованной осью абсцисс и прямой 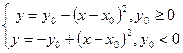 . Расположить точки данного множества в соответствии с убыванием значений заданной функции.
. Расположить точки данного множества в соответствии с убыванием значений заданной функции.
Сортировку произвести:
33. методом обмена;
34. методом вставкой;
35. методом выбора;
36. челночным методом.
37 – 40. Даны два массива A и B вещественных чисел по N элементов. Считая, что массивы представляют единую последовательность из (2N) чисел, отсортировать массивы по возрастанию. Примечание: использовать дополнительный массив для слияния заданных массивов нельзя.
Сортировку массивов произвести:
37. методом обмена;
38. методом вставкой;
39. методом выбора;
40. челночным методом.
41 – 44. В результате эксперимента получено n пар значений величин x и y в массивах X ( n ) и Y ( n ). Массив X не упорядочен, но не содержит одинаковых элементов. Получить значения функции y ( x ) с постоянным шагом  , где
, где  и
и  - соотвественно наибольшее и наименьшее значения в массиве X . Значения y с постоянным шагом вычислить по формуле линейной интерполяции соседних наблюдений (после упорядочения по x):
- соотвественно наибольшее и наименьшее значения в массиве X . Значения y с постоянным шагом вычислить по формуле линейной интерполяции соседних наблюдений (после упорядочения по x):
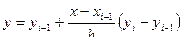 .
.
Сортировку массива X произвести:
41. методом обмена;
42. методом вставкой;
43. методом выбора;
44. челночным методом.
45 – 48. В результате эксперимента получены наборы значений аргумента x и соответствующих значений функции y. Сформировать третий массив 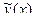 по возрастанию значений аргумента из значений функции
по возрастанию значений аргумента из значений функции 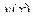 . Если одному значению x соответствует несколько значений y, взять их среднее значение.
. Если одному значению x соответствует несколько значений y, взять их среднее значение.
Сортировку массива аргумента осуществить:
45. методом обмена;
46. методом вставкой;
47. методом выбора;
48. челночным методом.
49 – 50. В неупорядоченном массиве из N элементов есть совпадающие значения. Вначале упорядочить массив по убыванию, а затем из каждой группы одинаковых элементов оставить только один, удалив остальные и поджав массив к его началу.
Сортировку массива осуществить:
49. методом вставкой;
50. челночным методом.
Лабораторная работа №5
Динамическими массивами
Цель работы: закрепить практические навыки работы с системой программирования языка С++ на примере реализации алгоритмов над динамическими многомерными массивами.
Основные теоретические сведения
Указатели
Указатель – это переменная, значение которой равно значению адреса памяти, по которому лежит значение некоторой другой переменной. В этом смысле имя этой другой переменной отсылает к ее значению прямо, а указатель – косвенно. Ссылка на значение посредством указателя называется косвенной адресацией.
Указатели в языке Си делятся на два вида: указатели на объекты и указатели на функции. Свойства и правила их использования различны.
Указатели, подобно любым другим переменным, перед своим использованием должны быть объявлены. Объявление указателя на объект имеет вид:
тип *имя_указателя;
где тип – один из предопределенных или определенных пользователем типов, а имя_указателя – указатель.
Например,
int *APtr;
объявляет переменную APtr типа int * (т.е указатель на целое число) и читается следующем образом: “ APtr является указателем на объект целочисленного типа”. Каждая переменная, объявляемая как указатель, должна иметь перед собой символ (*), который обозначает операцию косвенной адресации.
При объявлении указателя возможна его инициализация. Имеется две формы инициализации указателя:
1) тип *имя_указателя=инициализирующее_значение
2) тип *имя_указателя (инициализирующее_значение)
В качестве инициализирующего_значения может использоваться:
- явно заданный участок памяти
double *cc=0x1047;
- указатель, уже имеющий значение
float *ca;
…
float *cb=ca;
- выражение, позволяющее получить адрес объекта с помощью операции ссылки (&)
int a;
…
int *ce=&a;
Указатели должны инициализироваться либо при своем объявлении, либо с помощью оператора присваивания. Использовать указатель без присвоения ему какого-нибудь участка памяти нельзя. Указатель может получить в качестве начального значения 0 или NULL. Указатель с начальным значением 0 или NULL ни на что не указывает. NULL – это символическая константа, определенная специально для цели показать, что данный указатель ни на что не указывает. Пример объявления указателя с его инициализацией:
int *countPtr = NULL;
Для присваивания указателю адреса некоторой переменной используется операция адресации & (операция ссылки), которая возвращает адрес своего операнда. Например, если имеются объявления
int y = 5;
int *yPtr, x;
то оператор
yPtr = &y;
присваивает адрес переменной y указателю yPtr.
Присвоив указателю адрес конкретного участка памяти, можно с помощью операции разыменования не только получать, но и изменять содержимое этого участка памяти. Для этого используется операция разыменования * (операция косвенной адресации). Она возвращает значение объекта, на который указывает ее операнд (т.е. указатель).
Если присвоить указателю адрес конкретного объекта или значение уже инициализированного указателя, то это превратит запись *имя_указателя в синоним уже имеющегося имени объекта. Запись,
double z;
double *A=&z;
double *C, *D;
C=&z;
D=A;
превратит *A, *C, *D в синонимы переменной z. Изменяя значение, лежащее по адресу на которое указывают указатели, автоматически изменяется значение переменной, так как указатели A, C, D и переменная z связаны между собой одним участком памяти. Продолжая начатый пример
z=6;
double A1, C1, D1;
A1=*A;
C1=*C;
D1=*D;
присвоит переменным A1, C1, D1 значение 6, т.е. значение переменной z, на которую указывают указатели A, C, D.
Операции new и delete
Чтобы связать неинициализированный участок памяти, еще не занятым никаким объектом программы, используется оператор new:
указатель= new тип (инициализирующее_значение);
Операция возвращает указатель на динамически размещенный в памяти объект, т.е. предоставляет указателю память под объект заданного типа. Пример
double *A=new double;
int *B;
B=new int;
объявляет указатели и выделяет им свободное место, не занятое никаким объектом.
Инициализирующее_значение задает начальные значения создаваемого объекта. Запись
double *C=new double (-1.8);
предоставляет место указателю С под объект вещественного типа и инициализирует его, т.е. записывает начальное значение -1.8.
Если операция new возвратила нулевое значение адреса – NULL, то это значит, что операционная система не может выделить память под данный объект, поэтому после использования оператора new желательно всегда проверять адрес выделенного участка памяти
double *A;
A=new double;
if (A==NULL) …
Динамически распределенную память следует освобождать, когда отпадает необходимость в размещенных в ней объектах. Освобождение памяти осуществляется с помощью операции delete, которая имеет следующий синтаксис
delete имя_указателя;
Пример
int *B=new int;
…
delete B;
объявляет указатель, выделяя и освобождая место под объект в адресном пространстве.
Освобождение памяти уничтожает сам объект, а не указатель. В дальнейшем, указателю можно заново выделить участок памяти под новый объект и освободить эту память, что позволяет более гибко использовать оперативное адресное пространство компьютера. Поэтому, объекты созданные с помощью операции new называются динамическими.
long *P;
…
P=new long;
…
delete P;
…
P=new long;
…
delete P;
Операция delete освобождает память, но сама не задает указателю значение NULL, поэтому во избежание использования в дальнейшем неинициализированного указателя желательно это делать программно.
delete P;
P=NULL;
Операции над указателями
Указатели могут применяться как операнды в арифметических выражениях, выражениях присваивания и выражениях сравнения. Однако, не все операции, обычно используемые в этих выражениях, разрешены применительно к переменным указателям.
С указателями может выполняться ограниченное количество арифметических операций. Указатель можно увеличивать (++), уменьшать (--), складывать с указателем целые числа (+ или +=), вычитать из него целые числа (- или -=) или вычитать один указатель из другого.
Сложение указателей с целыми числами отличается от обычной арифметики. Прибавить к указателю 1 означает сдвинуть его на число байтов, содержащихся в переменной, на которую он указывал. Обычно подобные операции применяются к указателям на массивы. Например, запись
int *Pt;
…
Pt+=2;
увеличит значение Pt (т.е. адрес в памяти, на который указывает Pt), не на два, а на четыре байта, так как один объект целочисленного типа int в памяти занимает два байта.
Аналогичные правила действуют и при вычитании из указателя целого значения.
Однако при использовании арифметических операций над указателями нельзя полагать, чтоб две переменные – указатели одинакового типа будут находится в памяти вплотную друг к другу, если только они не соседствуют в массиве.
Сравнение указателей операциями >, <, >=, <= также имеют смысл только для указателей на один и тот же массив. Однако, операции отношения == и != имеют смысл для любых указателей. При этом указатели равны, если они указывают на один и тот же адрес в памяти.
Указатель можно присваивать другому указателю, если оба указателя имеют одинаковый тип. В противном случае нужно использовать операцию приведения типа, чтобы преобразовать значение указателя в правой части присваивания к типу указателя в левой части присваивания. Исключением из этого правила является указатель на void (т.е. void*), который является общим указателем, способным представлять указатели любого типа. Указателю на void можно присваивать все типы указателей без приведения типа. Однако указатель на void не может быть присвоен непосредственно указателю другого типа – указатель на void сначала должен быть приведен к типу соответствующего указателя.
Связь массивов и указателей
Массивы и указатели Си++ тесно связаны и могут быть использованы почти эквивалентно. При определении массива, имя массива является указателем константой, значением которой служит адрес первого элемента массива (с индексом 0), а запись
имя_массива[индекс]
является выражением с двумя операндами. Первый из них, т.е. имя_массива – константный указатель – адрес начала массива в основной памяти, а индекс – это выражение целого типа, определяющее смещение от начала массива.
Используя операцию обращения по адресу * (операция разыменования), действие бинарной операции можно представить следующим образом:
*(имя_массива + индекс)
т.е. операндами для операции [] служат имя_массива и индекс. Из этого становится очевидным, почему индекс первого элемента массива равен нулю. Таким образом, запись *имя_массива – обращение к первому элементу массива, *(имя_массива+1) – обращение ко второму, и т.д.
Поскольку сложение *(имя_массива+индекс) коммутативно, то возможна такая эквивалентная запись *(индекс+имя_массива) и, следовательно, индекс [имя_массива] именует тот же элемент массива, что имя_массива [индекс].
В некоторых конструкциях можно использовать выражение имя_массива [индекс] с отрицательным значением индекса. В этом случае имя_массива должен указывать не на начало массива, т.е. не на его нулевой элемент.
Ссылки
Ссылки – это специальный тип указателя, который позволяет работать с указателем как с объектом. Объявление ссылки делается с помощью операции ссылки, обозначаемой амперсантом (&) – тем же символом, который используется для адресации. Например, если имеется объявление
double*P = new double;
то можно создать ссылку на этот объект оператором:
double& Ref = *P;
Объявленная таким образом переменная Ref является ссылкой на объект вещественного типа. Она может рассматриваться как псевдоним объекта. Эта переменная является именно указателем, а не самим объектом. Но работа с ней производится как с объектом, в отличие от указателя.
*P=*P+0.5;
Ref=Ref+0.5;
Чаще всего ссылки используются при передаче в функции параметров по ссылке.
Примеры программ, реализующие алгоритмы работы с динамическими массивами
Пример 1. Даны три одномерных массива А, B , C, состоящие из N вещественных значений. Сформировать массив K такой же длины, элементы которого вычисляются по формуле 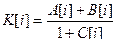 . Если
. Если  , то
, то 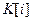 принять равным нулю. Заполнение массивов A, B , C осуществить с помощью датчика случайных чисел.
принять равным нулю. Заполнение массивов A, B , C осуществить с помощью датчика случайных чисел.
#include<iostream.h>
#include<stdlib.h>
#include<conio.h>
main()
{
int i,N;
double *A,*B,*C;
cout<<"Введите N=";
cin>>N;
A=new double [N];
B=new double [N];
C=new double [N];
for(i=0; i<N; i++)
A[i]=double(random(101)-50)/10;
for(i=0; i<N; i++)
B[i]=double(random(101)-50)/10;
for(i=0; i<N; i++)
C[i]=double(random(101)-50)/10;
cout<<"Массив А:"<<endl;
for(i=0; i<N; i++)
cout<<"A["<<i<<"]="
<<A[i]<<endl;
cout<<"Массив B:"<<endl;
for(i=0; i<N; i++)
cout<<"B["<<i<<"]="
<<B[i]<<endl;
cout<<"Массив C:"<<endl;
for(i=0; i<N; i++)
cout<<"C["<<i<<"]="
<<C[i]<<endl;
double *K=new double[N];
for(i=0; i<N; i++)
if (1+C[i]) K[i]=(A[i]+B[i])/(1+C[i]);
else K[i]=0;
cout<<"Массив K:"<<endl;
for(i=0; i<N; i++)
cout<<"K["<<i<<"]="
<<K[i]<<endl;
delete []A;
delete []B;
delete []C;
delete []K;
getch();
}
Пример 2. Сформировать квадратную матрицу порядка N по правилу 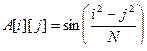 и подсчитать количество положительных элементов в ней.
и подсчитать количество положительных элементов в ней.
#include<iostream.h>
#include<stdlib.h>
#include<conio.h>
#include<math.h>
main()
{
int N;
cout<<"Введите размерность матрицы"<<endl;
cout<<"N=";
cin>>N;
double** A=new double* [N];
int i,j;
for (i=0; i<N; i++)
A[i]=new double [N];
for (i=0;i<N; i++)
for (j=0; j<N; j++)
A[i][j]=sin(double(i*i-j*j)/N);
for (i=0;i<N; i++){
for (j=0; j<N; j++)
cout <<A[i][j]<<" ";
cout<<endl;
}
int kol=0;
for (i=0;i<N; i++)
for (j=0; j<N; j++)
if(A[i][j]>0) kol++;
cout<<"Положительных значений = "<<kol;
getch();
}
Пример 3. Дан двумерный массив натуральных чисел размером (  ). Не создавая дополнительных массивов, определить в каждой строке двумерного массива, какой из элементов повторяется наибольшее число раз, и найти его порядковый номер первого появления в строке. Заполнение двумерного массива осуществить с помощью ввода с клавиатуры.
). Не создавая дополнительных массивов, определить в каждой строке двумерного массива, какой из элементов повторяется наибольшее число раз, и найти его порядковый номер первого появления в строке. Заполнение двумерного массива осуществить с помощью ввода с клавиатуры.
#include<iostream.h>
#include<stdlib.h>
#include<conio.h>
main()
{
int N,M;
cout<<"N=";
cin>>N;
cout<<"M=";
cin>>M;
int **A=new int* [N];
int i,j;
for(int i=0; i<N; i++)
A[i]=new int [M];
for(i=0;i<N;i++)
{cout<<"Введите "<<i+1<<" строку:"<<endl;
for(j=0;j<M;j++)
{cout<<"A["<<i<<"]["<<j<<"]=";
cin>>A[i][j];
}
}
clrscr();
for(i=0;i<N;i++)
{cout<<endl;
for(j=0;j<M;j++)
cout<<A[i][j]<<" ";
}
cout<<endl;
int index, count,count_max,m;
for(i=0;i<N;i++)
{count_max=0;
index=0;
for (j=0; j<M; j++)
{count=0;
for (m=j+1; m<M; m++)
if (A[i][j]==A[i][m]) count++;
if(count>count_max) {count_max=count;
index=j;
}
}
cout<<"В "<<i+1<<"строке "
<<index<<" элемент повторяется "
<<count_max+1<<" раз"<<endl;
}
getch();
}
Варианты заданий
ЗАДАНИЕ I:
1. Заполнить массив следующим образом:
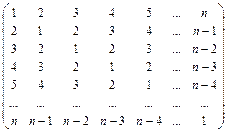 ,
,
n – нечетное.
2. Заполнить массив следующим образом:
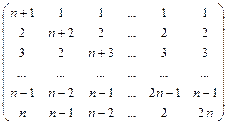 ,
,
n – четное.
3. Строки матрицы А(m, n) заполнить не полностью: в массиве L( m ) указать количество элементов в каждой строке. Переслать элементы матрицы построчно в начало одномерного массива Т( m ∙ n), подсчитать их количество.
4. Сформировать квадратную матрицу порядка  следующим образом (n – четное):
следующим образом (n – четное):

5. Сформировать квадратную матрицу порядка 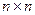 следующим образом:
следующим образом:

6. Матрицу М(m, n) заполнить натуральными числами от 1 до 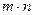 по спирали, начинающейся в левом верхнем углу и закрученной почасовой стрелке.
по спирали, начинающейся в левом верхнем углу и закрученной почасовой стрелке.
7. Сформировать квадратную матрицу порядка 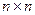 следующим образом (n – четное):
следующим образом (n – четное):

8. Построить квадратную матрицу следующим образом:

9. Ввод элементов матрицы А(m, n) осуществляется в произвольном порядке тройками чисел < i, j, A ij>. Признаком конца ввода служат три нуля: <0, 0, 0>. Проверить корректность такого ввода: все ли элементы введены, нет ли попытки повторного ввода или указания несуществующих координат i и j. Указание. Разрешается выделение дополнительного (рабочего) массива такой же размерности, что и исходный массив, для хранения признаков «заполненности» элементов матрицы
10. Заполнить массив следующим образом:
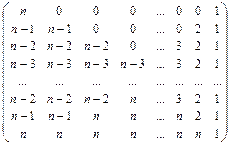 ,
,
n – четное.
11. Заполнить массив следующим образом:
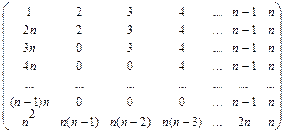 ,
,
n – нечетное.
12. Матрица А вводится с клавиатуры, построчно. Число строк заранее неизвестно, но различных строк не более m. Расположить строки в выделенном массиве, при этом повторяющиеся строки включать единожды.
13. Сформировать квадратную матрицу порядка  следующим образом (n – четное):
следующим образом (n – четное):

14. Дано вещественное число x. Получить квадратную матрицу порядка n +1:

15. Заполнить массив следующим образом:
 ,
,
n – нечетное.
16. Матрицу К(m, n) заполнить следующим образом. Элементам, находящимся на периферии (по периметру матрицы), присвоить значение 1; периметру оставшейся подматрицы — значение 2 и так далее до заполнения всей матрицы.
17. Заполнить массив следующим образом:
 ,
,
n – четное.
18. Получить матрицу

19. Получить квадратную матрицу порядка n:
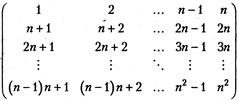
20. Матрицу А(m, n) заполнить следующим образом. Для заданных k и l элементу akl присвоить значение 1; элементам, окаймляющим его (соседним с ним по вертикали, горизонтали и диагоналям) — значение 2; элементам следующего окаймления — значение 3 и так далее до заполнения всей матрицы. Примечание. Алгоритм не изменится, если координаты элемента (несуществующего) k и l находятся за пределами матрицы.
21. Заполнить массив следующим образом:
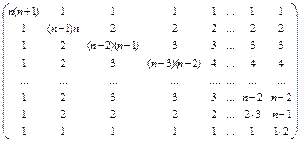 ,
,
n – четное.
22. Сформировать квадратную матрицу порядка  следующим образом (n – четное):
следующим образом (n – четное):

23. Сформировать квадратную матрицу порядка  следующим образом:
следующим образом:

24. Выполнить операцию транспонирования прямоугольной матрицы А( m , n ), 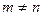 и, не выделяя дополнительного массива для хранения результата. Матрицу А( m , n ) заполнить целочисленными случайными значениями от -100 до 100.
и, не выделяя дополнительного массива для хранения результата. Матрицу А( m , n ) заполнить целочисленными случайными значениями от -100 до 100.
25. Даны вещественные числа  . Получить квадратную матрицу порядка n:
. Получить квадратную матрицу порядка n:
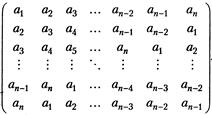
26. Сформировать квадратную матрицу порядка 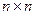 следующим образом:
следующим образом:

27. Найти произведение матриц А(m, n) и В( n , k): С( m ,k) = AxB. Матрицы А и B заполнить целочисленными случайными значениями от -10 до 10.
28. Задан одномерный массив  . Получить вещественную квадратную матрицу порядка n:
. Получить вещественную квадратную матрицу порядка n:

29. Заполнить массив следующим образом:
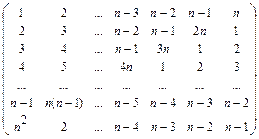 ,
,
n – нечетное.
30. Матрицу А(n, п) разложить на слагаемые: A = B+C+D, где В — строго нижнетреугольная, С — диагональная, D — строго верхнетреугольная матрицы того же размера. Матрицу A заполнить целочисленными случайными значениями от -20 до 20.
31. Заполнить массив следующим образом:
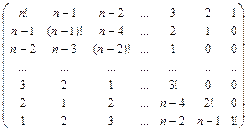 ,
,
n – нечетное
32. Заполнить массив следующим образом:
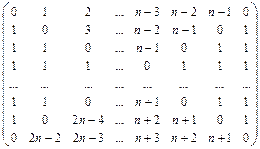 ,
,
n – четное.
33. Найти определитель заданной матрицы n-го порядка методом Гаусса (в любой модификации). Матрицу A заполнить вещественными случайными значениями от -20 до 20.
34. Задан одномерный массив  . Получить вещественную квадратную матрицу порядка n:
. Получить вещественную квадратную матрицу порядка n:

35. Сформировать квадратную матрицу порядка  следующим образом:
следующим образом:

36. Найти матрицу, обратную заданной А(п, п), методом Гаусса (в любой модификации). Матрицу A заполнить вещественными случайными значениями от 0 до 100.
37. Сформировать квадратную матрицу порядка  следующим образом (n – четное):
следующим образом (n – четное):

38. Сформировать квадратную матрицу порядка 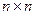 следующим образом (n – четное):
следующим образом (n – четное):

39. Привести матрицу А(m, n) к трапециевидной, используя метод Гаусса, при этом не обязательно т<п. Матрицу A заполнить вещественными случайными значениями от 0 до 100.
40. Сформировать квадратную матрицу порядка 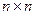 следующим образом (n – четное):
следующим образом (n – четное):

41. Матрица А(п, п+1), системы линейных уравнений АХ=В приведена к верхнетреугольному виду. Найти вектор решения X последовательной подстановкой. Матрицу A заполнить вещественными значениями вводом с клавиатуры.
42. Найти ранг прямоугольной матрицы А(т, n) методом Гаусса. Матрицу A заполнить вещественными случайными значениями от 0 до 100.
43. Для заданной матрицы А(m, n) найти ее произведение на транспонированную к ней AA-1. Матрицу A заполнить целочисленными случайными значениями от -50 до 50.
44. Заполнить матрицу А(m, n) простыми числами.
ЗАДАНИЕ II:
1. Дана целочисленная матрица размера M x N. Строки матрицы назовем похожими, если совпадают множества чисел, встречающихся в этих строках. Найти количество похожих строк в матрице.
2. Дана целочисленная матрица размера M x N. Найти количество ее столбцов, все элементы которых различны.
3. Дана целочисленная матрица размера M x N. Вывести номер ее первой строки, содержащей максимальное количество одинаковых элементов.
4. Дана квадратная матрица порядка M. Найти набольшее и наименьшее значение сумм элементов матрицы, параллельных главной и побочной диагоналей.
5. Дана квадратная матрица порядка M. Найти наибольшее значение из минимальных элементов каждой диагонали, параллельной главной.
6. Дана квадратная матрица порядка M. Повернуть ее на 90, 180 и 270 градусов в положительном направлении.
7. Дана матрица размера M x N. Вывести количество столбцов, элементы которых монотонно возрастают.
8. Дана матрица размера M x N. Найти минимальный среди элементов тех строк, которые упорядочены либо по возрастанию, либо по убыванию.
9. Дана целочисленная матрица размера M x N. Найти элемент, являющийся максимальным в своей строке и минимальным в своем столбце.
10. Дана матрица размера M x N. Элемент называется локальным минимумом, если он меньше всех окружающих его элементов. Заменить все локальные минимумы данной матрицы на 0.
11. Дана матрица размера M x N. Поменять местами ее столбцы так, чтобы их минимальные элементы образовывали возрастающую последовательность.
12. Дана матрица А размером M x N.. Определить k — количество особых элементов массива А, считая его элемент особым, если он больше суммы остальных элементов его столбца.
13. Элемент матрицы назовем седловой точкой, если он является наименьшим в своей строке и одновременно наибольшим в своем столбце или, наоборот, является наибольшим в своей строке и наименьшим в своем столбце. Для заданной целой матрицы размером M x N напечатать индексы всех ее седловых точек.
14. Задана матрица размером M x N. Найти максимальный по модулю элемент матрицы. Переставить строки и столбцы матрицы таким образом, чтобы максимальный по модулю элемент был расположен на пересечении i – й строки и k – то столбца.
15. Дана целая квадратная матрица n - го порядка. Определить, является ли она магическим квадратом, т.е. такой, в которой суммы элементов во всех строках и столбцах одинаковы. Получить транспонированную матрицу. Сформировать одномерный массив из ее диагональных элементов. Найти след матрицы, суммируя элементы одномерного массива.
16. Квадратная матрица, симметричная относительно главной диагонали, задана верхним треугольником в виде одномерного массива. Восстановить исходную матрицу и напечатать по строкам.
17. Дана квадратная целочисленная матрица порядка п. Сформировать результирующий одномерный массив, элементами которого являются строчные суммы тех строк, которые начинаются с k идущих подряд положительных чисел.
18. Дана целочисленная матрица размером M x N. Элемент матрицы называется среднестатистическим по k – му параметру, если на нем достигается минимум модуля разности среднего арифметического чисел из k -го столбца и k – ой строки. Элемент называется самым средним, если он является среднестатистическим по самому большому количеству параметров. В данной матрице определить пять самых средних элементов.
19. Прямоугольное поле разбито на M x N квадратных клеток. Некоторые клетки покрашены в черный цвет. Известно, что все черные клетки могут быть разбиты на несколько непересекающихся и не имеющих общих вершин черных прямоугольников. Считая, что цвета клеток даны в виде массива M x N, значения элементов которого равны либо 0, либо 1. Подсчитать число черных прямоугольников, о которых шла речь. Число действий должно быть порядка M x N.
Указание. Число прямоугольников равно числу их левых верхних углов. Является ли клетка верхним углом, можно узнать, посмотрев на ее цвет, а также цвет верхнего и левого соседей. (Не забудьте, что их может не быть, если клетка с краю.)
20. Даны квадратная таблица A [ N , N ] и число М< N. Для каждого квадрата размером M x M этой таблице вычислить сумму стоящих в нем чисел.
Указание. Сначала для каждого горизонтального прямоугольника размером Мх 1 вычислить сумму стоящих в нем чисел. (При сдвиге такого прямоугольника по горизонтали на 1 нужно добавить одно число и одно вычесть.) Затем, используя эти суммы, вычислить суммы в квадратах. (При сдвиге квадрата по вертикали добавляется полоска, а другая полоска убавляется.)
21. Среди тех строк и столбцов целочисленной матрицы, которые содержат только нечетные элементы, найти строку или столбец с максимальной и минимальной суммой модулей элементов.
22. Подсчитать количество строк заданной целочисленной матрицы NxN , являющихся перестановкой чисел 1, 2, ..., N (т.е.содержащих каждое из чисел 1, 2, ..., N ровно один раз).
23. Среди строк и столбцов заданной целочисленной матрицы, содержащих только такие элементы, которые по модулю не больше 10, найти столбец или строку с минимальным и максимальным произведением элементов.
24. Целочисленным массивом кодируется поле, на котором расположены несколько прямоугольников. Прямоугольники не накладываются друг на друга и не соприкасаются. Разные прямоугольники состоят из разных значений. Один и тот же прямоугольник не может состоять из различных значений. Пустые квадраты поля кодируются значением 0. Подсчитать число прямоугольников разных значений.
Пример :
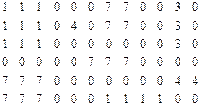
Для этого поля программа должна выдать ответ:
1-прямоугольников: 2
7-прямоугольников: 3
3-прямоугольников: 1
4-прямоугольников: 2
25. Характеристикой столбца целочисленной матрицы назовем сумму модулей его отрицательных нечетных элементов. Переставляя столбцы заданной матрицы, расположить их в соответствии с ростом характеристик.
26. Для заданной квадратной матрицы найти такие k , что k -я строка матрицы совпадает с k -м столбцом.
27. Найти максимальный элемент среди всех элементов тех строк заданной матрицы, которые упорядочены (либо по возрастанию, либо по убыванию).
28. Расстояние между k – й и l – й строками квадратной матрицы А ( NxN ) определяется как
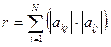
Найти строки заданной матрицы, максимально удаленные друг от друга.
29. Определить, является ли заданная матрица ортонормированной, т. е. равно ли скалярное произведение каждой пары различных строк (столбцов) нулю.
30. Определить номера строк матрицы, в которых знаки элементов чередуются.
31. В целочисленной матрице M x N требуется каждый элемент заданной матрицы заменить минимальным элементом, выбираемым среди элементов, стоящих не ниже и не правее этого элемента, включая его значение.
32. Даны мозаичные изображения замочной скважины и ключа. Пройдет ли ключ в скважину? То есть даны матрицы 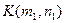 и
и 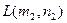 ,
,  ,
,  , состоящие из нулей и единиц. Проверить можно ли наложить матрицу L на матрицу K (без поворота, разрешается только сдвиг) так, чтобы каждой единице матрицы L соответствовал нуль матрицы K, и если можно, то как (на сколько и в каком направлении следует подвинуть матрицу L по матрице K до выполнения условия)?
, состоящие из нулей и единиц. Проверить можно ли наложить матрицу L на матрицу K (без поворота, разрешается только сдвиг) так, чтобы каждой единице матрицы L соответствовал нуль матрицы K, и если можно, то как (на сколько и в каком направлении следует подвинуть матрицу L по матрице K до выполнения условия)?
33. В целочисленной матрице M x N каждый элемент (кроме граничных) заменить суммой непосредственно примыкающих к нему элементов по вертикали, горизонтали и диагонали.
34. Матрица M x N состоит из нулей и единиц. Найти в ней самую длинную цепочку подряд стоящих нулей по горизонтали, вертикали или диагонали.
35. Дана целочисленная матрица размером M x N. Найти все числа, каждое из которых встречается в каждой строке матрицы, и все числа, повторяющиеся более чем в одном столбце матрицы.
36. Клеточное поле размером M x N есть результат игры в крестики и нолики на “бесконечном поле”. Проверить, не закончена ли игра выигрышем. Считается, игра закончена, если на поле найдется по горизонтали, вертикали или диагонали цепочка, состоящая подряд из 5 крестиков или ноликов. (Значение 0 соответствует нолику, 1 соответствует крестику, 2 – пустой клетки.)
37. Дана целочисленная матрица размером M x N, состоящая из нулей и единиц. Найти квадрат наибольшего значения (квадратную подматрицу), состоящий из нулей или единиц.
38. Дана целочисленная матрица размера M x N. Различные столбцы матрицы назовем похожими, если совпадают множества чисел, встречающихся в этих столбцах. Найти количество столбцов, похожих на последний столбец.
39. Дана целочисленная матрица размера M x N. Найти количество ее строк, все элементы которых различны.
40. Дана целочисленная матрица размера M x N. Вывести номер его последнего столбца, содержащего максимальное количество одинаковых элементов.
41. Дана квадратная матрица порядка M. Вывести максимальные из элементов каждой ее диагонали, параллельной побочной.
42. Дана матрица размера M x N. Вывести количество строк, элементы которых монотонно убывают.
43. Дана матрица размера M x N. Найти максимальный среди элементов тех столбцов, которые упорядочены либо по возрастанию, либо по убыванию. Если такие столбцы отсутствуют, то вывести 0.
44. Дана матрица размера M x N. Элемент называется локальным максимумом, если он больше всех окружающих его элементов. Заменить все локальные максимумы данной матрицы на 0.
45. Дана матрица размера M x N. Поменять местами ее строки так, чтобы их максимальные элементы образовывали убывающую последовательность.
46. Дана целочисленная матрица размером M x N. Элемент матрицы называется уникальным по k – му параметру, если на нем достигается максимум модуля разности среднего арифметического чисел из k -го столбца и k – ой строки. Элемент называется самым уникальным, если он является среднестатистическим по самому большому количеству параметров. В данной матрице определить пять самых средних элементов.
47. Каждый элемент а( i , j ) матрицы A ( m , n ) заменить суммой элементов подматрицы A ’( i , j ), расположенной в правом нижнем углу матрицы. Заполнение начать с конца матрицы.
Лабораторная работа №6
Массивами символов
Цель работы: закрепить практические навыки работы с системой программирования языка С++ на примере реализации алгоритмов над массивами символов.
Массивы символов
В отличие от других языков программирования, стандарт языка Си не содержит специального типа строк. Строки представляются одномерными массивами символов, т.е. массивами элементов типа char. Но если длина массивов чисел имеет определенный значимый характер, то длина строк постоянно меняется и не всегда, получается, иметь информацию об ее длине. Поэтому, для определения длины строки был введен специальный нулевой символ ‘\0’, который обозначает конец строки в массиве в не зависимости от начальной выделенной для него памяти. В этом случае, число хранимых символов в строке всегда на 1 больше числа значащих символов. Если нулевой символ отсутствует, то обработка строки будет продолжаться до тех пор, пока в памяти не встретится случайный нулевой символ.
Таким образом, строка в языке Си рассматривается, как массив символов, оканчивающийся нулевым символом (`\0`), в не зависимости от длины.
Строка может быть объявлена либо как просто массив символов
char St[] = “строка”;
либо как переменная указатель типа char*
char *Sp = “строка”;
Каждое из этих приведенных эквивалентных объявлений присваивает строковой переменной начальное значение “строка”, а длина при этом определяется автоматически компилятором и равна 7 элементам, содержащих соответственно символы: ‘с’, ‘т’, ‘р’, ‘о’, ‘к’, ‘а’ и '\0'. Можно объявлять строковые переменные заданной длины. Например, операторы
char Str[100];
char *Stp=new char [100];
объявляют переменные, которые могут содержать строки до 99 значащих символов плюс заключительный нулевой символ.
Доступ к отдельным символам строки осуществляется по индексам, начинающимся с нуля. Например, St[0] и Sp[0] – первые символы объявленных выше строк, St[5] и Sp[5] – последние, а St[6] и Sp[6] содержат нулевые символы.
Так как, строка представляется массивом, то доступ к ней осуществляется через указатель или указатель - константу, который является адресом ее первого символа, поэтому при работе со строками необходимо учитывать общие правила работы с указателями и с массивами, так запись
Str=“переменная”;
или
Str=St;
вызовет ошибку компилятора, потому что, во первых – нельзя присваивать значение указателю – константе, а во вторых – St, Str, Sp и Stp содержат лишь адрес на участок памяти по которому располагается набор символов, а не сам этот набор. Присваивание литералы – константы возможно лишь только при объявлении строки.
Так же, следует помнить, что резервирование памяти полностью лежит на программисте, а при работе с указателем на строку этот указатель должен указывать на выделенный ранее участок памяти.
Примеры программ, реализующие алгоритмы работы с массивами символов
Пример 1. Дана строка, содержащая текст. Определить слова, в которых количество согласных меньше, чем в предыдущем слове, а количество гласных больше, чем в последующем.
#include<iostream.h>
#include<stdlib.h>
#include<conio.h>
#include<string.h>
main()
{
char *str=new char [100];
char *work=new char [100];
char *next,*current,*previous;
int gl_next,gl_current,sg_current,sg_previous;
int i,j;
int log;
char gl[]={128,133,136,142,147,155,157,158,159,
160,165,168,174,227,235,237,238,239,0};
char *s;
cin.get(str,100);
s=str;
do
{
while (s&&(*s==' '||*s==','||*s=='.'))
s++;
next=NULL;
current=NULL;
previous=NULL;
strcpy(work,s);
previous=strtok(work,". ,");
if (previous)current=strtok(NULL,". ,");
if (current)next=strtok(NULL,". ,");
if (previous&¤t&&next)
{
sg_previous=0;
sg_current=0;
gl_current=0;
gl_next=0;
i=0;
while (previous[i])
{log=(unsigned char) previous[i]>=128
&&
(unsigned char)previous[i]<=175;
log=log||((unsigned char)previous[i]>=224
&&
(unsigned char)previous[i]<=239);
if(log)
{
for(j=0;j<strlen(gl);j++)
if (previous[i]==gl[j]) break;
if(j==strlen(gl)) sg_previous++;
}
i++;
}
i=0;
while (current[i])
{log=(unsigned char)current[i]>=128
&&
(unsigned char)current[i]<=175;
log=log||((unsigned char)current[i]>=224
&&
(unsigned char)current[i]<=239);
if(log)
{
for(j=0;j<strlen(gl);j++)
if (current[i]==gl[j])
{
gl_current++;
break;
}
if(j==strlen(gl)) sg_current++;
}
i++;
}
i=0;
while (next[i])
{log=(unsigned char)next[i]>=128
&&
(unsigned char)next[i]<=175;
log=log||((unsigned char)next[i]>=224
&&
(unsigned char)next[i]<=239);
if(log)
for(j=0;j<strlen(gl);j++)
if (next[i]==gl[j])
{
gl_next++;
break;
}
i++;
}
log=sg_previous>sg_current&&gl_current>gl_next;
if (log) cout<<"Найденное слово: "<<current<<endl;
}
s=strpbrk(s,". ,");
}
while(next);
getch();
}
ЗАДАНИЕ I:
1. Дана строка, содержащая текст. Найти длину самого короткого и самого длинного слова.
2. Дана строка, содержащая текст, заканчивающийся точкой. Вывести на экран составляющие ее слова из трех букв.
3. Дана строка, содержащая текст. Определить, сколько в нем слов, заканчивающихся гласными буквами.
4. Дана строка, содержащая текст. Указать те слова, которые содержат хотя бы одну букву из звонких согласных.
5. Дана строка, содержащая текст. Найти в ней те слова, которые начинаются и оканчиваются одной и той же буквой.
6. Дана строка, содержащая текст. Вывести, в скольких словах этого текста встречаются гласные буквы. Ответ должен приводиться в грамматически правильной форме, например «а — 5 слов», «о — 3 слово» и т. д.
7. Дана строка, содержащая текст. Найти слова в тексте, которые можно составить из первого и последнего слова (буквы можно использовать не более одного раза).
8. Дана строка, содержащая текст в виде чисел, записанных в римской нотации, и разделенных знаками препинания. Найти самое наибольшее число.
9. Дана строка, содержащих текст из двух предложений. Найти слова, которые встречаются в каждом из двух заданных предложений.
10. Дана строка, содержащая текст. Вывести слова в алфавитном порядке.
11. Дана строка, содержащая текст. Найти те буквы, которые встречаются в каждом слове и только один раз.
12. Дана строка, содержащая текст. Часто встречающаяся ошибка начинающих наборщиков — дважды записанное подряд слово. Обнаружить в тексте такие ошибки.
13. Дана строка, содержащая текст. Найти слова в тексте, которые являются анаграммами с первым или последним словом. Анаграммы – пара слов, при прочтении каждого из которых в обратном направлении образуется другое слово пары, например, (ПОЛК, КЛОП); (БАР, РАБ).
14. Дана строка, содержащая текст. В данном тексте найти самое наибольшее слово из тех, длина которых больше двух. (Пример: Варвар> Академия).
15. Один из способов идентификации автора литературного произведения — подсчет частоты вхождения отдельных слов. В заданном тексте найти наиболее часто встречающееся слово.
16. В русском языке, как правило, после букв Ж, Ч, Ш, Щ пишется И, А, У, а не Ы, Я, Ю. Проверить заданный текст на соблюдение этого правила и вывести слова с ошибками (с учетом исключений: ЖЮРИ, БРОШЮРА, ПАРАШЮТ).
17. «Латинизатор кириллицы»-. При интернет-общении с русской диаспорой в других странах часто возникают проблемы отсутствия кириллицы у зарубежных респондентов, а также слабое знание иностранных языков у соотечественников. Один из выходов — набор русских слов похожими по начертанию буквами латинского алфавита. Среди прописных русских букв таких насчитывается одиннадцать: А, В, Е, К, М, Н, О, Р, С, Т, X. В заданном тексте выбрать те русские слова, которые
без искажения могут быть написаны латинскими буквами.
18. Дана строка, содержащая текст. Найти слова в тексте, которые являются палиндромами с первым или последним словом. (Палиндром - это выражение, которое читается одинакова слева направо и справа налево).
19. Дана строка, содержащая текст. Найти слова, которые содержат только одну гласную букву.
20. Дана строка, содержащая текст. Найти те слова в тексте, перед которыми в последовательности находятся только меньшие (по алфавиту) слова, а за ними - только большие;
21. Дана строка, содержащая текст. Найти слова в тексте, которые встречаются в последовательности по одному разу;
22. Дана строка, содержащая текст. Найти симметричные слова в тексте.
23. Даны две строки, содержащие текст. Найти и распечатать самые длинные слова, общие для этих строк. Если нужных слов нет – сообщить об этом.
24. Дана строка, содержащая текст. Определить пары слов в строке, расстояние между которыми наименьшее. (Расстояние между словами – это количество позиций, в которых слова различаются. Например, расстояние между словами МАМА и ПАПА или МЫШКА и КОШКА равно двум).
25. Дана строка, содержащая текст. Определить слова в строке, в которых либо буквы упорядочены по алфавиту, либо каждая буква входит в слово не менее двух раз (т.е. слова типа МАМА и ПАПА).
26. Дана строка, содержащая текст. Составить частотный словарь текста. Вывести его по алфавиту, а справа от каждого слова – частоту, с которой оно встретилось.
27. Дана строка, содержащая текст. Определить слова с наибольшим количеством различных пар букв. (Например, в слове babacabacd 5 различных пар букв.)
28. Дана строка, содержащая текст. Найти слово в тексте, длина которого наиболее близко к средней длине всех слов в тексте.
29. Во введенном тексте указать слово, в котором доля гласных в отношении к согласным составляет примерно столько же, сколько во всем тексте.
30. Во введенном тексте найти слова, которые могут быть полностью составлены из других слов с помощью конкатенации. (Например, БАЛКОН=БАЛ+КОН).
31. Во введенном тексте найти группы слов, записанных одними и теми же буквами и отличающиеся только их порядком, т.е. перестановкой. (Например, КОМАР, КОРМА).
32. Дана строка, содержащая текст. Определить все слова, в которых использованы только буквы, имеющиеся в заданном слове.
33. Во введенном тексте определить самое длинное слово, в котором все буквы разные.
34. Даны две строки, содержащие текст. Для этих двух строк найти самую длинную общую подстроку. Пробелы и знаки препинания игнорировать, строчные и прописные буквы считать неразличимыми.
35. Дан текст, содержащий слова, разделенные пробелами. Определить, какие буквы в словах совпадают чаще: первые, последние или средние. Позиция средней буквы в слове определяется по формуле: позиция_средней_буквы=(длина_слова mod 2) +1.
36. Дан текст, содержащий слова из букв и цифр. Определить произведение чисел в каждом слове, а затем найти сумму получившихся чисел.
37. Даны две строки, содержащие текст. Найти самое длинное слово из тех слов, которые встречаются в обеих строках.
38. Даны две строки, содержащие текст. Найти самое короткое слово из тех слов, которые не повторяются в обеих строках.
39. Дана строка, содержащая текст. В данном тексте найти самое наименьшее слово из тех, которые содержат более одной гласной. (Пример: Балкон > Балка).
40. Дана строка, содержащая текст. Найти слова, в которых буквы распложены по алфавиту. (Например: Абель).
41. Дана строка, содержащая текст. Определить, длина каких слов больше, четных или нечетных.
42. Дана строка, содержащая текст. Найти слово с наименьшим количеством гласных из первой половины текста, и с наибольшим количеством из второй. Если количество слов нечетно, то среднее слово во внимание не брать.
43. Дана строка, содержащая текст. Определить слово с наибольшим количеством одинаковых букв.
44. Дана строка, содержащая текст. Найти слова, в которых присутствуют буквы первого слова, но не присутствуют буквы последнего слова.
45. Дана строка, содержащая текст. Определить букву, которая встречается в наименьшем количестве слов.
46. Дана строка, содержащая текст. Определить в тексте длины одинаковых слов и их количество.
47. Дана строка, содержащая текст. Найти слово с наибольшим количеством букв, которые не встречаются в других словах.
48. Дана строка, содержащая текст. Определить, расположены ли в тексте слова по алфавиту, и каким образом, по убыванию или возрастанию.
49. Дана строка, содержащая текст. Определить буквы, которые встречаются в четных словах и не встречаются в нечетных.
50. Дана строка, содержащая текст. Определить, расположены ли в тексте слова по убыванию или возрастанию своих длин.
ЗАДАНИЕ II:
1. Дана строка, содержащая текст. Преобразовать строку так, чтобы все буквы в словах были отсортированы по алфавиту.
2. Дана строка, содержащая текст. Преобразовать строку так, чтобы все слова в ней стали идентификаторами, слова состоящие только из цифр и слова, которые начинаются с цифры - удалить.
3. Дана строка, содержащая текст. Преобразовать строку таким образом, чтобы в ее начале были записаны слова, содержащие только цифры, потом слова, содержащие только буквы, а затем слова, которые содержат и буквы и цифры.
4. Дана строка, содержащая текст. Преобразовать строку таким образом, чтобы все слова в ней были напечатаны наоборот.
5. Дана строка, содержащая текст. Отредактировать заданное предложение, удаляя из него те слова, которые встречаются в предложении несколько раз.
6. Дана строка, содержащая текст. Отредактировать заданное предложение, удаляя из него все слова с нечетными номерами и переворачивая слова с четными номерами.
7. Дана строка, содержащая текст. Удалить из нее каждое слово нечетной длины.
8. Дана строка, содержащая текст. В каждом слове переставить его первую букву на место последней. При этом вторую, третью,..., последнюю буквы сдвинуть влево на одну позицию, то есть осуществить циклический сдвиг влево.
9. Перенос. Примем следующие правила переноса русских слов: в каждой из разделяемых частей должно быть более одной буквы, из которых хотя бы одна — гласная;
- нельзя разделять согласную и следующую за ней гласную;
- буквы И, Ь, Ъ считать согласными, но перенос последних допустим.
Преобразовать текст таким образом, что в каждом из вводимых слов были поставлены все возможные знаки переноса, например: СЕ-ЛЬ-С-КО-ХО-ЗЯЙ-С-Т-ВЕ-Н-НАЯ. Строчные и прописные буквы считать неразличимыми.
10. Дана строка, содержащая текст. Переставить слова в тексте так, чтобы каждое следующее слово начиналось с той буквы, на которую закончилось предыдущее. Первое слово оставить на месте.
11. Дана строка, содержащая текст. Расставить слова в соответствии с алфавитом.
12. Дана строка, содержащая текст. Изменить порядок букв в словах на противоположный.
13. Дана строка, содержащая текст. Преобразовать строку, содержащую эти же слова, но расположенные в обратном порядке.
14. Дана строка, содержащая текст. Преобразовать каждое слово в строке, удалив из него все последующие вхождения первых двух букв этого слова.
15. Дана строка, содержащая текст и число k (0 < k < 10). Зашифровать строку, выполнив циклическую замену каждой буквы на букву того же регистра, расположенную в алфавите на k-й позиции после шифруемой буквы (например, для k = 2 "А" перейдет в "В", "а" — в "в", "Б" — в "Г", "я" — в "б" и т.д.). Букву "ё" в алфавите не учитывать, знаки препинания и пробелы не изменять.
16. Дана строка-предложение. Зашифровать ее, поместив вначале все символы, расположенные на четных местах, а затем, в обратном порядке, все символы, расположенные на нечетных местах (например, строка "Программа" превратится в "ргамамроП").
17. Даны две строки, содержащие текст из чисел, разделенные пробелами. Сформировать третью строку из сумм чисел, соответствующих порядковому номеру в строках. Если в одной строке чисел меньше, чем в другой, т.е. числу одной строки не будет соответствовать по порядковому номеру число другой строки, то это число оставить без изменений. (Например: “123 34 56 7 89”, “2 45 90 8” -> “125 79 146 15 89”).
18. Дана строка, содержащая текст. Преобразовать строку, удалив из нее слова, которые состоят менее чем из трех букв.
19. Осуществить шифрование и дешифрование введенного текста. Шифрование произвести следующим образом: записать текст в матрицу по строкам, а затем переписать по спирали от центра. Количество строк и столбцов в матрице должно быть нечетным, а недостающие значения букв заполнить случайным образом.
20. Дана строка, содержащая текст. Преобразовать слова, отличные от последнего следующим образом:
а) перенести последнюю букву в начало слова;
б) оставить в слове только первые вхождения каждой буквы.
21. Дано целочисленное арифметическое выражение, записанное как строка, в десятичной системе счисления. Проверить правильность записи и вычислить значение этого выражения. Выражение записывается без скобок, операции выполняются в порядке их следования.
22. Даны две строки, содержащие текст. Выделить из первой строки все слова, начинающиеся с гласной буквы, а из второй строки все слова, начинающиеся с согласной буквы. Образовать новую строку, состоящую из выделенных слов, так чтобы первым было слово из второй строки, затем из первой, потом из второй и т.д.
23. Дана строка, содержащая фамилии и инициалы студентов. Преобразовать текст, оставив лишь фамилии. Также требуется напечатать список студентов с указанием для каждого количества его однофамильцев.
24. Дана строка, содержащая текст. Преобразовать текст следующим образом: заменить в каждом слове первую встреченную букву ‘a’ буквой ‘o’, удалив все остальные. Если в слове нет такой буквы, оставить его без изменений.
25. Дана строка, содержащая текст. Преобразовать текст, удалив из него все кратные рядом стоящие символы, оставив по одному. (Например: ПППОООГГОДДДАААА -> ПОГОДА).
26. Дана строка, содержащая текст. Преобразовать слова, удалив из них одну среднюю букву, если длина слова нечетная, или две средних, если длина четная.
27. Произвести объединение двух строк, т.е. создать третью строку, состоящую из всех слов принадлежащих первой строке и из всех слов принадлежащих второй строке, за исключением повторяющихся.
28. Произвести пересечение двух строк, т.е. создать третью строку, состоящую из слов принадлежащих одновременно и первой и второй строке.
29. Произвести разность двух строк, т.е. создать третью строку, состоящую из слов принадлежащих первой строке и не принадлежащих второй строке.
30. Реализовать шифр подстановки, с помощью квадрата Полибия. Алфавит исходного сообщения записывается в виде матрицы, и каждая буква сообщения кодируется парой чисел (строка, столбец). Произвести кодирование и декодирование исходного сообщения на основе матрицы-ключа. Закодированное сообщение должно быть представлено символьной строкой.
31. Реализовать многобуквенную систему шифрования, с помощью таблицы Вижинера. Выбирается слово-ключ, которое записывается с повторениями над буквами сообщения. Буква зашифрованного сообщения находится на пересечении строки (буквы исходного сообщения) и столбца (буквы ключа) в таблице Вижинера. Произвести кодирование и декодирование исходного сообщения на основе слова-ключа. Таблица Вижинера:
| А | Б | … | Ю | Я |
| Б | В | … | Я | А |
| … | … | … | … | … |
| Ю | Я | … | Ь | Э |
| Я | А | … | Э | Ю |
32. Реализовать шифр Цезаря с ключом. Выбирается слово-ключ, которое записывается с повторениями над буквами сообщения. Занумеровать алфавит исходного сообщения и ключа. Номер буквы зашифрованного сообщения находится как сумма по модулю длины алфавита сообщения и ключа. Произвести кодирование и декодирование исходного сообщения на основе слова-ключа для алфавита из букв, знаков препинания и цифр.
33. Реализовать парный шифр. Ключом является фраза, содержащая не менее половины разных букв алфавита исходного сообщения. Подписывая под этими буквами буквы в алфавитном порядке, не вошедшие в ключ, получаем разбиение букв алфавита на пары. Кодирование - замена каждой буквы исходного сообщения на ее парную. Произвести кодирование и декодирование исходного сообщения на основе слова-ключа для алфавита из букв, знаков препинания и цифр.
34. Реализовать XOR-кодирование. Представить исходное сообщение и ключ в двоичном виде. Кодирование и декодирование происходит следующим образом: каждый бит сообщения преобразуется с использованием нового бита ключа по следующему правилу: 0+0=0, 0+1=1, 1+0=1, 1+1=0. Произвести кодирование и декодирование исходного сообщения на основе слова-ключа для алфавита из букв, знаков препинания и цифр.
35. Реализовать шифрование с помощью постолбцовую транспозицию. Выбирается слово-ключ. Формируется матрица, с числом столбцов равным числу букв в ключе. Исходное сообщение посимвольно заносится в эту матрицу. Затем столбцы этой матрицы переставляются в соответствии с алфавитным порядком букв слова-ключа. Произвести кодирование и декодирование исходного сообщения на основе слова-ключа для алфавита из букв, знаков препинания и цифр.
36. Дана строка, содержащая текст. Преобразовать все слова следующим образом: переставить первую букву на место последней, вторую на место первой, третью на место второй и т.д., т.е. осуществить циклический сдвиг влево.
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ:
| 1. | Подбельский В.В. Язык Си++. Учебное пособие. – М: Финанасы и статистика, 1992. – 600 с. |
| 2. | Громов Ю. Ю., Татаренко С. И. Программирование на языке СИ: Учебное пособие.- Тамбов, 1995.- 144 с. |
| 3. | Дерк Луис. Borland C++. Справочник / Пер. с нем. – М.: “Издательство БИНОМ”, 1997. – 560 с.: ил. |
| 4. | И.Г. Семакин, А.П. Шестаков Основы программирования: Учебник для сред. проф. образования. – 2-е изд., стер. – М.: Издательский центр “Академия”, 2003. – 432 с. |
| 5. | Д.А. Гуденко, Д.В. Петроченко Сборник задач по программированию. – СПб.: Питер, 2003. – 475 с.: ил. – (Серия “Компас”). |
| 6. | А.В. Крячков, И.В. Сухинина, В.К. Томшин Программирование на С и С++. Практикум: Учеб. пособие для вузов. – 2-е изд., исправ. – М.: Горячая линия. – Телеком, 2000. – 344 с.: ил. |
| 7. | А. Юркин Задачник по программированию. – СПб.: Питер, 2002. – 192 с. |
ПРИЛОЖЕНИЕ 1
СТАНДАРТНЫЕ БИБЛИОТЕКИ ФУНКЦИЙ ЯЗЫКА СИ
Таблица П1.1
Специальные функции
| Функция | Прототип и краткое описание действий | Местона-хождение прототипа |
| delay kbhit memcpm memcpy memicpm memmove memset nosound | viod delay ( unsigned x ); Приостанавливает выполнение программы на х мсек. int kbhit ( viod ); Возвращает ненулевое целое, если в буфере клавиатуры присутствуют коды нажатия клавиш, в противном случае – нулевое значение. int memcpm (const viod *s1, const viod *s2, unsigned n); Сравнивает посимвольно две области памяти s 1 и s 2 длинной n байт. Возвращает значение меньше нуля, если s 1< s 2, нуль, если s 1== s 2, и больше нуля, если s 1 > s 2. viod *memcpy (viod *p, const viod *i, unsigned n); Копирует блок длинной n байт из области памяти i в область памяти p. int memicpm (const viod *s1, const viod *s2, unsigned n); Подобн memcpm, за тем исключением, что игнорируются различия между буквами верхнего и нижнего регистра. viod *memmove (viod *dest, const viod *src, int n); Копирует блок длинной n байтов из src в dest. Возвращает указатель dest. viod *memset (viod *s, int c, unsigned n); Записывает во все байты области памяти s значение с. Длинна области s равна n байт. viod nosound ( viod ); Прекращает подачу звукового сигнала, начатую функцией sound (). | dos.h conio.h mem.h mem.h mem.h mem.h mem.h dos.h |
| Продолжение табл. П.1.7 | ||
| Функция | Прототип и краткое описание действий | Местона-хождение прототипа |
| peek peekb poke pokeb rand signal sound srand | int peek (unsigned s, unsigned c); Возвращает целое значение (слово), записанное в сегменте s со смещением с. char peekb (unsigned s, unsigned c); Возвращает один байт, записанный в сегменте s со смещением с, т.е. по адресу s : c. viod poke (unsigned s, unsigned c, int v); Помещает значение v в слово сегмента s со смещением с, т.е. по адресу s : c. viod pokeb (unsigned s, unsigned c, char v); То же, что и poke, но помещает один байт v по адресу s : c. int rand ( void ); Возвращает псевдослучайное целое число из диапазона 0 ÷ (2ⁿ -1), где n=15, может использовать функцию srand (). int signal ( int sig ); Вызывает программный сигнал с номером sig. Используется для обработки исключительных ситуаций в языке Си. viod sound ( unsigned f ); Вызывает звуковой сигнал с частотой f Гц. viod srand ( unsigned seed ); Функция инициализации генератора случайных чисел ( rand ); seed – любое беззнаковое целое число. | dos.h dos.h dos.h dos.h stdlib.h signal.h dos.h stdlib.h |
Таблица П1.8
Функции – манипуляторы
| Манипулятор | Краткое описание действий |
| dec hex oct ws endl ends fluch | Устанавливает десятичное основание системы счисления. Устанавливает шестнадцатеричное основание системы счисления. Устанавливает восьмеричное основание системы счисления. При вводе позволяет извлекать из входного потока обобщенные пробельные символы. При выводе помещает в поток символ новой строки и флэширует буфер потока. При выводе помещает в поток символ конца строки’\0’ Флэширует буфер потока ostream. |
Таблица П1.14
Таблица П1.15
Режимы файла,
ПРИЛОЖЕНИЕ 2
ТАБЛИЦА ASCII – КОДОВ СИМВОЛОВ
Таблица П1.18
Полная таблица десятичных, шестнадцатеричных и двоичных ASCII - кодов
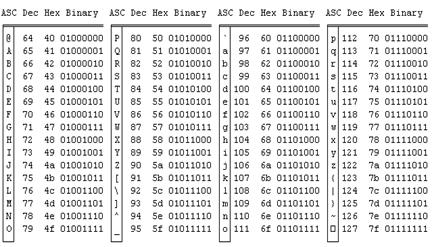
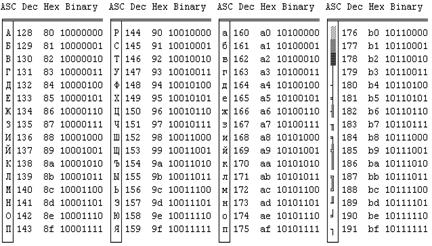
Продолжение табл. П1.18
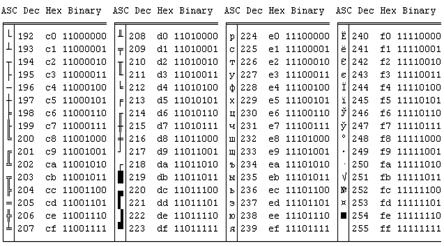
С.А. Дьяконица
Д.С. Семенов
ОСНОВЫ ПРОГРАММИРОВАНИЯ НА ЯЗЫКЕ C ++
Методические указания к лабораторным работам по дисциплине
Лабораторный практикум
Братск
УДК 681.3.06
Основы программирования на языке С++: Методические указания к лабораторным работам / С.А. Дьяконица, Д.С. Семенов. – Братск: БрГУ, 2007. – с.
Содержат указания к выполнению цикла лабораторных работ, а также основным понятиям, принципам и приемам разработки программ на языке С++.
Предназначены для студентов дневной, заочной форм обучения и обучающихся по сокращенным образовательным программам специальности.
Рецензент:
к.т.н. Крумин О.К.А.Н. Емцев, канд. техн. наук,
профессор кафедры систем электроснабжения
Печатается по решению издательско-библиотечного совета
| 665709, Братск, ул. Макаренко, 40, Братский государственный ун-т Тираж 100 экз. Заказ |
| |
СОДЕРЖАНИЕ
| Введение…………………………………………..……............ | 4 |
| Лабораторная работа №1 Программирование алгоритмов линейной структуры………………………….. | 5 |
| Лабораторная работа №2 Программирование алгоритмов разветвляющейся структуры……………… | 36 |
| Лабораторная работа №3 Программирование алгоритмов циклической структуры……………………… | 58 |
| Лабораторная работа №4 Программирование алгоритмов над статическими массивами……………… | 79 |
| Лабораторная работа №5 Программирование алгоритмов над многомерными динамическими массивами…………….... | 106 |
| Лабораторная работа №6 Программирование алгоритмов над массивами символов……………………... | 135 |
| Список используемых источников………………………… | 151 |
| Приложение 1. Стандартные библиотеки функций языка Си……………………………………………………… | 152 |
| Приложение 2. Таблица ASCII – кодов символов……… | 172 |
ВВЕДЕНИЕ
Практическому программированию нельзя научиться теоретически, без решения задач на ЭВМ. Целью практикума является закрепление теоретического материала, изучение технических приемов составления и отладки программ, привитие навыков практического программирования на языке Си++, изучение и использование наиболее важных численных методов.
Практикум предусматривает прохождение всех ступеней начального программирования: понимание задачи, разработку алгоритма, составление и подготовку программы к работе на ЭВМ, отладку программы, счет и анализ результатов. Он может быть использован, как студентами, самостоятельно изучающими программирование, так и преподавателями для организации лабораторных работ.
Практикум включает 6 лабораторных работ, каждая из которых посвящена конкретной теме.
В начале каждой лабораторной работы приведены теоретические сведения с примерами типовых задач. Все примеры написаны в стиле ANSI и протестированы с использованием компилятора Borland C++. Разбор этих решений поможет в написании собственных программ, в освоении некоторых полезных технических приемов, приобретении определенного стиля программирования.
Лабораторная работа №1
Программирование алгоритмов линейной структуры
Цель работы: выработать практические навыки работы с системой программирования языка Си/Си++, научиться создавать, вводить в компьютер, выполнять и исправлять простейшие программы на языке Си/Си++ в режиме диалога, познакомиться с диагностическими сообщениями компилятора об ошибках при выполнении линейных программ.
Дата: 2019-02-02, просмотров: 510.