6.3.1. Исходные данные, необходимые для проведения
параметрического синтеза
Рассмотрим сущность параметрического синтеза и возможные методы, используемые на практике при его проведении. Наибольшую ценность представляет ЛП-метод, идеи которого были известны, но долгое время не находили применения в силу ряда причин. Модификация его позволяет представить данный метод в виде конкретного алгоритма, для которого нужны следующие исходные данные:
математическая модель проектируемого объекта (РСЗО, РК), подсистемы, элемента;
набор оптимизируемых параметров 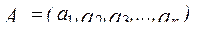 ;
;
параметрические ограничения (явные) в виде пределов изменения каждого параметра 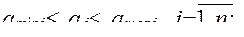
функциональные ограничения (неявные) вида
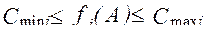 ;
;
где 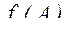 - некоторые функции от параметров
- некоторые функции от параметров 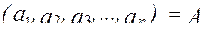 . Причем, в большинстве случаев функциональные ограничения часто представляют (задают) в виде функционалов;
. Причем, в большинстве случаев функциональные ограничения часто представляют (задают) в виде функционалов;
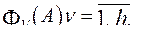 - набор критериев качества проектируемого объекта, подсистемы, элемента.
- набор критериев качества проектируемого объекта, подсистемы, элемента.
Кроме этого, в качестве исходных данных следует рассматривать конкретную методику, т.е. последовательность выполнения элементарных процедур, обеспечивающих оптимизацию структуры объекта проектирования. Например, для модифицированного ЛП-метода такими процедурами являются следующие.
1. Расчет критериев качества при заданных значениях параметров. Каждый расчет критериев называют (считают) испытанием, а набор параметров при этом - пробной точкой. При i -м испытании выполняются определенные действия со стороны проектировщика.
2. Настройка метода выбора параметров на заданное n их количество и на номер j-го испытания.
3. Выбор i-й пробной точки из n-мерного пространства параметров 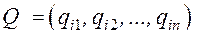 , где значения
, где значения 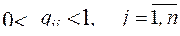 т.е. пронормированные. Такой способ обеспечивает равномерный обзор (перебор) всего пространства параметров при сравнительно небольшом числе испытаний.
т.е. пронормированные. Такой способ обеспечивает равномерный обзор (перебор) всего пространства параметров при сравнительно небольшом числе испытаний.
4. Расчет пробной точки, удовлетворяющей параметрическим ограничениям
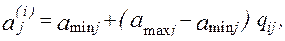
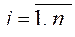
5. Проверка тех функциональных ограничений, которые не зависят от результатов математического моделирования. Если ограничения не выполнены, то осуществляется переход к следующему испытанию.
6. Вычисление критериев качества. Их расчет в основном связан с методами и алгоритмами анализа влияния заданных параметров на исследуемые математической моделью физические процессы. В связи с этим необходим формализованный блок исследования математической модели объекта проектирования (РСЗО, РК или их подсистем, элементов).
7. Проверка тех функциональных ограничений, которые зависят от результатов математического моделирования.
8. Построение таблиц испытаний (по полученным значениям каждого критерия), в которых критерии качества располагают в порядке убывания, т.е. первой стоит лучшая модель по данному критерию. Каждой модели соответствует определенный 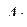 - набор параметров, зашифрованный в номере i-го испытания.
- набор параметров, зашифрованный в номере i-го испытания.
При завершении метода проектировщику представляется для анализа и принятия решений таблица испытаний. В диалоге с ЭВМ конструктор может изменить исходные данные и продолжить заполнение таблицы испытаний.
Процедура выбора i-й пробной точки n-мерного пространства 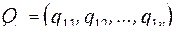 может осуществляться в определенном порядке, которая хорошо зарекомендовала себя на практике и включает ряд пунктов.
может осуществляться в определенном порядке, которая хорошо зарекомендовала себя на практике и включает ряд пунктов.
1. Номер i-й точки представляется в двоичной системе счисления
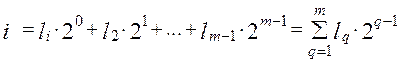
Здесь 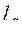 равно либо 0, либо 1.Например,
равно либо 0, либо 1.Например,
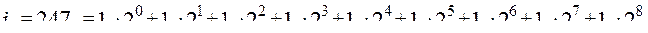
2. Для каждого j -го параметра из таблицы 21 выбирается набор коэффициентов 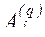 и вычисляются значения
и вычисляются значения
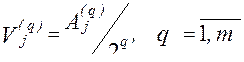
3 .Определяются значения j-го параметра по зависимости
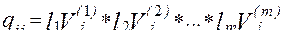
Операция (*) означает поразрядное сложение по модулю 2 в двоичной системе, т.е. десятичное число 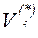 (умножается на 0 или 1) преобразуется в двоичное и между двоичными представлениями чисел происходит операция (*).
(умножается на 0 или 1) преобразуется в двоичное и между двоичными представлениями чисел происходит операция (*).
Необходимо отметить, что имеется несколько алгоритмов реализации указанной процедуры выбора i -й пробной точки n-мерного пространства и несколько вариантов оценки потребного количества пробных точек.
Таблица 21
Коэффициенты А j для варьирования параметров
| q j | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 3 | 5 | 15 | 17 | 51 | 65 | 255 | 257 | 771 | 1285 | 3855 | 4369 |
| 3 | 1 | 1 | 7 | 11 | 13 | 61 | 67 | 79 | 465 | 721 | 823 | 4091 | 4125 |
| 4 | 1 | 3 | 1 | 5 | 31 | 29 | 81 | 147 | 433 | 149 | 719 | 3693 | 3841 |
| 5 | 1 | 1 | 5 | 3 | 15 | 59 | 25 | 141 | 177 | 759 | 267 | 1839 | 6229 |
| 6 | 1 | 3 | 7 | 7 | 9 | 11 | 79 | 63 | 193 | 707 | 1351 | 1479 | 6857 |
| 7 | 1 | 1 | 3 | 11 | 7 | 31 | 13 | 161 | 309 | 901 | 2007 | 1311 | 6235 |
| 8 | 1 | 3 | 3 | 13 | 23 | 57 | 11 | 219 | 101 | 687 | 449 | 579 | 3779 |
| 9 | 1 | 1 | 1 | 15 | 11 | 29 | 13 | 85 | 475 | 63 | 1233 | 337 | 6577 |
| 10 | 1 | 3 | 5 | 1 | 29 | 61 | 79 | 169 | 293 | 177 | 689 | 2259 | 2197 |
| 11 | 1 | 1 | 7 | 5 | 5 | 3 | 127 | 97 | 47 | 819 | 765 | 3341 | 3379 |
| 12 | 1 | 3 | 1 | 11 | 25 | 15 | 9 | 191 | 417 | 631 | 789 | 1327 | 2885 |
| 13 | 1 | 1 | 5 | 7 | 19 | 51 | 51 | 151 | 157 | 141 | 389 | 901 | 5889 |
| 14 | 1 | 3 | 7 | 9 | 3 | 43 | 33 | 35 | 231 | 553 | 1327 | 3039 | 3073 |
| 15 | 1 | 1 | 3 | 1 | 21 | 27 | 119 | 175 | 413 | 891 | 931 | 413 | 7821 |
| 16 | 1 | 3 | 3 | 3 | 27 | 53 | 85 | 175 | 95 | 951 | 1151 | 3057 | 3249 |
| 17 | 1 | 1 | 1 | 7 | 1 | 13 | 115 | 223 | 391 | 385 | 651 | 1939 | 2029 |
| 18 | 1 | 3 | 5 | 9 | 17 | 33 | 51 | 149 | 95 | 711 | 1743 | 2667 | 3645 |
| 19 | 1 | 1 | 7 | 15 | 13 | 59 | 35 | 11 | 189 | 825 | 171 | 1833 | 1405 |
| 20 | 1 | 3 | 1 | 3 | 31 | 7 | 99 | 97 | 419 | 929 | 1699 | 575 | 5991 |
На практике наибольшее распространение получи вариант, сущность которого поясняется ниже. Считается, что таблица испытаний должна содержать N строк и чтобы ее сформировав требуется осуществить переход от одного испытания к другому. При 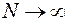 пробные точки образуют равномерно распределенную последовательность. Каким значением N ограничиться? Однозначного ответа нет, так как выбор величины N зависит от количества параметров (от размера пространства параметров) и заданной точности просмотра (зондирования) пространства параметров, от времени получения одной строчки таблицы испытаний, которое складывается из совокупности этапных времен. Кроме того, на выбор N оказывают влияние и функциональные ограничения, которые отбраковывают пробные точки. В качестве оценки N снизу рекомендуется брать (из опыта использования метода) значение
пробные точки образуют равномерно распределенную последовательность. Каким значением N ограничиться? Однозначного ответа нет, так как выбор величины N зависит от количества параметров (от размера пространства параметров) и заданной точности просмотра (зондирования) пространства параметров, от времени получения одной строчки таблицы испытаний, которое складывается из совокупности этапных времен. Кроме того, на выбор N оказывают влияние и функциональные ограничения, которые отбраковывают пробные точки. В качестве оценки N снизу рекомендуется брать (из опыта использования метода) значение 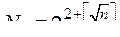 , где
, где 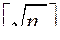 - целая часть числа z; n - количество оптимизируемых параметров.
- целая часть числа z; n - количество оптимизируемых параметров.
6.3.2. Алгоритм решения задачи параметрического синтеза
Общая схема алгоритма дается в качестве исходных данных (как одна из составляющих системы исходных данных). На основе ее по каждому критерию составляется табл. испытаний.
1. Значения критериев располагаются в порядке возрастания: 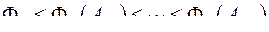 . Для каждого значения критерия указывается номер
. Для каждого значения критерия указывается номер 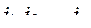 соответствующей пробной точки. Из такого построения таблиц следует, что при
соответствующей пробной точки. Из такого построения таблиц следует, что при 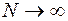 первое значение соответствует
первое значение соответствует 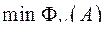 , а последнее -
, а последнее - 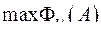 .
.
Напомним, что основная цель параметрического синтеза объектов проектирования заключается в определении оптимального варианта (из подмножества Парето, полученного в ходе структурного синтеза) с учетом всех противоречивых критериев качества. Обозначим через 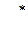 некоторый набор параметров, которым соответствуют критерии
некоторый набор параметров, которым соответствуют критерии 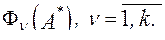 Допустим, что нашелся еще один набор параметров
Допустим, что нашелся еще один набор параметров 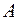 , для которого
, для которого
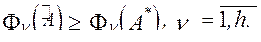
Причем хотя бы одно из неравенств являлось строгим. Очевидно» что 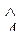 предпочтительнее
предпочтительнее 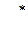 , поэтому
, поэтому 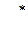 следует исключить из рассмотрения.
следует исключить из рассмотрения.
2. Таблицы испытаний позволяют:
учитывать столько критериев, сколько их необходимо для определения правильного функционирования объекта (подсистемы, элемента) и его оптимизации с позиции всех противоречивых критериев качества;
сократить исходную систему критериев качества и выбрать информативную подсистему критериев, характеризующих объект проектирования;
обосновать параметрические, функциональные и критериальные ограничения, определить допустимое и множество Парето - решений, проанализировать ресурсные возможности проектируемого объекта.
Разработчик, просматривая таблицы испытаний, назначает ограничения на критерии, для которых эти таблицы составлены. Обозначает через 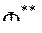 выбранные ограничения,
выбранные ограничения, 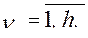
3. Проверяются непустоты множества допустимых точек в каждой таблице испытаний. Схема проверки заключается в следующем, Рассматривают таблицу для одного из критериев, например для первого критерия. Выбирают все пробные точки, для которых критерий удовлетворяет заданному ограничению, в данном случае 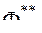 т.е. справедливо соотношение
т.е. справедливо соотношение
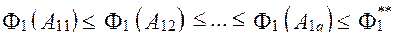
Выбранная точка 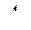 входят в множество допустимых, если дня имеют место одновременно
входят в множество допустимых, если дня имеют место одновременно 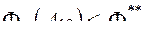
В случае пустоты множества возможны два выхода. Во-первых - изменить некоторые критериальные ограничения 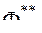 во-вторых (если разработчик не может менять
во-вторых (если разработчик не может менять 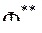 ) - увеличить количество пробных точек, т.е. продолжить построение таблиц испытаний. Если при многократном увеличении
) - увеличить количество пробных точек, т.е. продолжить построение таблиц испытаний. Если при многократном увеличении  точки
точки 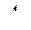 не образуют допустимого множества, то выбранные критериальные ограничения несовместимы.
не образуют допустимого множества, то выбранные критериальные ограничения несовместимы.
Процесс поиска множества допустимых точек можно рассматривать и с позиций сравнительной оценки вида
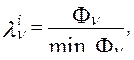
где 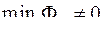 - наименьшее значение
- наименьшее значение 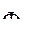 по всем пробным точкам (при изменении количества точек оно будет меняться);
по всем пробным точкам (при изменении количества точек оно будет меняться);
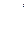 - значение критерия для i -и пробной точки.
- значение критерия для i -и пробной точки.
Оценка 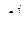 характеризует модель с точки зрения близости к наилучшему результату по каждому критерию (условно принимаем, что все критерии желательно минимизировать). Так как одна и та же модель в общем случае не является наилучшей (
характеризует модель с точки зрения близости к наилучшему результату по каждому критерию (условно принимаем, что все критерии желательно минимизировать). Так как одна и та же модель в общем случае не является наилучшей ( 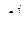 =1) по всем
=1) по всем 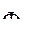 то в целях поиска компромиссного варианта, устанавливается допуск на отклонение
то в целях поиска компромиссного варианта, устанавливается допуск на отклонение 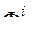 от
от 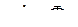 (или
(или 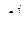 от 1), который называется критериальным допуском и обозначается
от 1), который называется критериальным допуском и обозначается 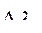 . Фактически еще при назначении
. Фактически еще при назначении 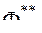 устанавливается
устанавливается 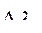 , так как
, так как
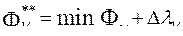 .
.
Однако вычисление 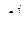 по приведенной выше формуле не всегда удобно. В ряде случаев целесообразно использовать зависимость вида
по приведенной выше формуле не всегда удобно. В ряде случаев целесообразно использовать зависимость вида
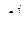 =
= 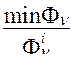 ,
,
а также вместо 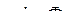 рассматривать в обоих случаях и
рассматривать в обоих случаях и 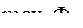
Модификации вычисления 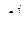 необходимо учитывать при обработке результатов эксперимента. Используя
необходимо учитывать при обработке результатов эксперимента. Используя 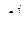 можно построить нормированные таблицы испытаний, в которых вместо абсолютных значений
можно построить нормированные таблицы испытаний, в которых вместо абсолютных значений 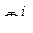 будут записаны относительные величины, т.е.
будут записаны относительные величины, т.е. 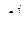
4. После определения множества компромиссных решений (допустимых точек) и нахождения 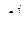 для всех этих решений перед разработчиком (проектировщиком) стоит задача выбора из них оптимального. Это делается на основе ранжирования критериев, выбора в результате этого одного из главных критериев, а с помощью его определение лучшего варианта объекта проектирования из компромиссных. При возникновении трудностей с назначением главного критерия на практике часто пользуются интегральным критерием, например
для всех этих решений перед разработчиком (проектировщиком) стоит задача выбора из них оптимального. Это делается на основе ранжирования критериев, выбора в результате этого одного из главных критериев, а с помощью его определение лучшего варианта объекта проектирования из компромиссных. При возникновении трудностей с назначением главного критерия на практике часто пользуются интегральным критерием, например
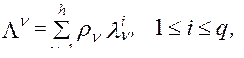
где 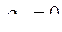 - коэффициенты важности частных критериев.
- коэффициенты важности частных критериев.
Суммирование осуществляется для каждой точки допустимого множества по всем критериям. Множество 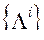 всегда имеет нижнюю границу. Для анализа результатов, как правило, строят нормированную таблицу, в которой варианты располагают в порядке значений
всегда имеет нижнюю границу. Для анализа результатов, как правило, строят нормированную таблицу, в которой варианты располагают в порядке значений 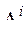 . Оптимальная модель (вариант) проектируемого объекта выбирается из условия
. Оптимальная модель (вариант) проектируемого объекта выбирается из условия  .
.
Таким образом, эти четыре этапа представляют конкретный алгоритм параметрического синтеза объекта при фиксированном количестве и наборе критериев. Но это только один из подходов - стандартный подход работы с таблицами испытаний. Комплексное исследование моделей (вариантов) с помощью таблиц испытаний состоит в проведении анализа, при котором меняются количество, состав критериев при постоянстве их числа, изменяются критериальные допуски и коэффициенты важности. Изменение количества критериев осуществляется не только за счет выбора их из числа сформулированных, но и на основе перевода некоторых ограничений в ранг критериев и, наоборот, перевод критериев в ограничения.
Работоспособность алгоритма рассмотрим на примере параметрического синтеза боевой части для перспективной РСЗО, которая обеспечивает пуск не только реактивных снарядов но и тактических ракет (прототип - американская система MLRS). В результате структурного синтеза получено множество вариантов БЧ интеллектуального типа (обеспечивают разведку местности и выдают координаты целей на соответствующие командные пункты). С помощью известных методов произведен отсев бесперспективных вариантов. Разработчики остановились на одном из вариантов, входящем в состав подмножества Парето.
С помощью экспертного опроса и сформирован перечень основных варьируемых параметров, из которых предстоит выбрать и назначены вариации границ каждого из параметров.
Рассмотрим частный пример определения качества элементов образцов РАВ с использованием интегральных показателей.
Пример. При проектировании самоходной пусковой установки перед разработчиками встала задача по выбору гидравлического насоса, обеспечивающего гидравлической энергией её механизмы. Выбор возможно осуществить из двух насосов, характеристики которых представлены в таблице 22.
В таблице 22 в первых семи строках приведены заданные величины, а в строках 8÷10 – результаты расчётов. Поясним их на примере насоса А.
Суммарная производительность насоса А за срок службы составит:
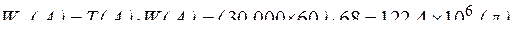 .
.
Суммарные затраты за срок службы составят:
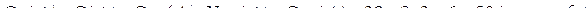 .
.
Интегральный показатель качества в данном случае определяется как отношение суммарных затрат к суммарной производительности, т.е.:
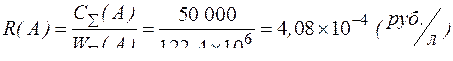 .
.
Из результатов проведенных расчётов (строка 10 табл. 22) видно, что насос Б обеспечивает более низкую стоимость одного произведённого литра рабочей жидкости (т.е. обладает более высоким значением интегрального показателя качества), а следовательно – обладает более высоким техническим уровнем, чем насос А.
Таблица 22
Дата: 2019-02-02, просмотров: 828.