6.2.1. Исходные данные, необходимые для проведения структурного синтеза
В сложившейся практике разработки сложных технических систем (в том числе АНО РК и РСЗО) исходные данные, потребные для проведения структурного синтеза, неотъемлемы от метода его осуществления. Последнее время широко применялся и постоянно совершенствовался морфологический метод. Родоначальником его является швейцарский астроном Ф.Цвикки, но использовал он данный метод совсем для других целей.
Под морфологией объекта понимают его построение, внутреннюю структуру, состав подсистем (элементов), способы образования объекта из различных подсистем (элементов), обеспечивающих выполнение всех задач (функций) в соответствии с его назначением и требуемыми характеристиками в заданных условиях эксплуатации. Отсюда следует, что в качестве исходных данных будут выступать различные сведения о предполагаемом объекте, условиях его применения и т.п.
В частности, к ним относятся:
задачи, которые должны решаться объектом (РСЗО, РК) в соответствии с его назначением;
внутренние процессы функционирования, взаимосвязь процессов функционирования;
внешние условия функционирования объекта, характеристика внешних воздействий, основные связи с другими объектами;
требуемые параметры процессов функционирования отдельных подсистем (элементов) и объекта в целом;
критерий качества выполнения операций и всего процесса функционирования объекта, а также различные ограничения;
функции номеров расчета (операторов) при управлении объектом в целом и при выполнении отдельных операций;
достижения науки и техники (в виде каталогов физических эффектов), определяющие способы реализации каждой функции объекта;
номенклатура функциональных и управляющих подсистем;
требования к параметрам процессов функционирования, выбранным критериям к ограничениям;
варианты (пути) технической реализации каждого выбранного типа подсистемы (элемента) с учетом их взаимосвязей в объекте и т.д.
На основе этих сведений разрабатывается морфологическая табл. определенного типа, которая в компактном вида содержит информацию. необходимую для проведения структурного синтеза, Упрощенный вариант ее представлен в таблице 18.
Опираясь на данные таблицы 18 можно осуществлять непосредственно структурный синтез объекта.
Как правило, число возможных вариантов структуры объекта и может превысить сотни и тысячи способов их реализации.
Задача стоит в «отсечении» бесперспективных вариантов с помощью методов, сущность которых рассматривалась ранее. Предварительно их (варианты) можно сократить при отборе возможных способов технической реализации подсистемы (элемента) анализа условий взаимосвязи физических эффектов.
В большинстве своем РСЗО и РК представляют собой суперсложные иерархические системы, характеризующиеся множеством не только подсистем (элементов), но и связей между ними.
Функционирование их как раз и основывается на проявлении множества взаимосвязанных физических эффектов (ФЭ). Очевидно, чтобы формировать морфологическую таблицу, необходимо знать условия взаимосвязей ФЭ. Как это делается можно найти в рекомендованной к занятию литературе. Наиболее общей и самой простой схемой взаимосвязи ФЭ является следящая схема.
Таблица 18
Исходные данные (вариант)
| Функции объекта | Тип подсистемы (элемента) | Возможный способ технической реализации подсистемы (элемента) |
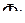
 ...
...
 ...
...
| 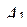
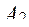 ...
...
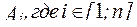 ...
...
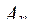
| 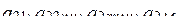
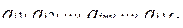 …
…
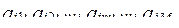 …
…
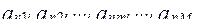
|
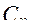
где 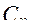 - множество результатов воздействия n-го ФЭ;
- множество результатов воздействия n-го ФЭ;
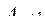 - множество воздействий (n+1) -го ФЭ.
- множество воздействий (n+1) -го ФЭ.
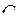
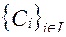 ,
,
где I - число номеров наименований результатов воздействий (n+1)-го ФЭ.
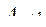 =
= 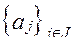 ,
,
где J- число номеров наименований воздействий (n+1)-го ФЭ.
При этом должно быть
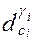
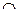
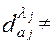 0
0
где 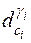 - значение результата воздействия n-го ФЭ;
- значение результата воздействия n-го ФЭ;
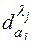 - значение воздействия
- значение воздействия 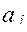 (n + 1)-го ФЭ;
(n + 1)-го ФЭ;
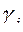 - множество номеров материалов, на которых проявляется
- множество номеров материалов, на которых проявляется  результатов
результатов
воздействия;
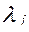 - множество номеров материалов, на которые оказывается
- множество номеров материалов, на которые оказывается
воздействие 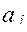 .
.
Несмотря на кажущуюся простоту, обоснование исходных данных для проведения структурного синтеза даже элемента (подсистемы) перспективного РК или РСЗО представляет долгую и кропотливую работу, требующую системных знаний во многих областях науки и техники. В этом можно убедиться на конкретных примерах, рассматриваемых далее. Следует отметить, что в ряде случаев при формировании морфологической таблицы целесообразно использовать меру сходства и различия между подсистемами, которые реализуют заданные функции. Это также способствует сокращению размерности решаемой задачи, позволяет упорядочить часть исходных данных.
Мерой сходства (близости) называется величина 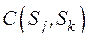 , имеющая предел и возрастающая с увеличением близости подсистем (элементов) по совокупности качественных признаков. Она обладает следующими свойствами
, имеющая предел и возрастающая с увеличением близости подсистем (элементов) по совокупности качественных признаков. Она обладает следующими свойствами
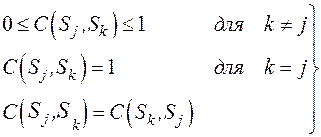 (41)
(41)
Здесь 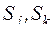 - множество качественных признаков, описывавших анализируемые подсистемы (элементы).
- множество качественных признаков, описывавших анализируемые подсистемы (элементы).
Мерой, противоположная мере сходства, называется мерой различия 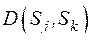 . Она также имеет характерные свойства:
. Она также имеет характерные свойства:
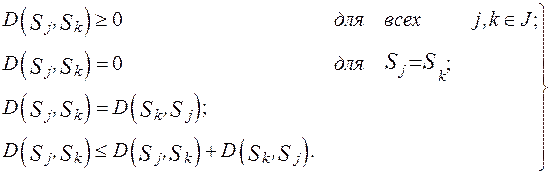 (42)
(42)
Свойствами (41) и (42) обладают формулы
 ;
;
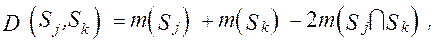
где 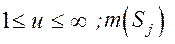 -обозначение числа элементов множества
-обозначение числа элементов множества 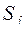
Приведенные формулы не являются единственными, но они нашли самое широкое распространение на практике в связи с интеллектуализацией процесса проектирования в различных конструкторских бюро, занимающихся разработкой перспективных РСЗО и РК.
6.2.2. Алгоритм решения задачи структурного синтеза
Рассмотрим алгоритм решения задачи структурного синтеза методом динамического программирования на конкретном примере. Допустим, что необходимо синтезировать структуру электропривода для перспективного РСЗО, которая должна включать в себя электродвигатель (ЭД), передаточный механизм (ПМ), исполнительный механизм (ИМ). Оптимальный вариант структуры электропривода должен гарантировать максимальную вероятность работ 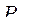 и удовлетворять ограничениям по стоимости
и удовлетворять ограничениям по стоимости 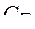 и массе
и массе 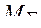 , т.е.
, т.е.
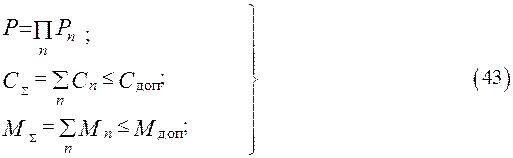
где 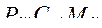 - вероятность безотказной работы, стоимость и масса n -ой
- вероятность безотказной работы, стоимость и масса n -ой
подсистемы, входящей в состав электропривода;
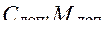 - допустимые значения стоимости и массы электропривода.
- допустимые значения стоимости и массы электропривода.
Варианты возможной технической реализации подсистем привода и их характеристики приведены в морфологической таблице 19.
Заданы допустимые значения стоимости и массы электропривода:
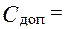 340 у.ед.;
340 у.ед.; 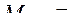 350 у.ед.
350 у.ед.
Морфологический граф электропривода и возможные взаимосвязи вариантов технической реализации подсистем показаны на рис. 93.
В соответствии с условиями задачи и ее математической формулировкой вида (41) на основе зависимостей
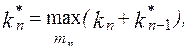
Таблица 19
Исходные данные
| Тип подсистемы | Вариант технической реализации | Характеристики | ||||
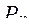
| 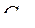 у.ед. у.ед.
| 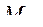 у.ед. у.ед.
| ||||
| ЭД |
| ЭД1 | 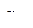
| 0,83 | 50 | 50 |
| ЭД2 | 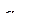
| 0,82 | 50 | 100 | ||
| ПМ |
| Гидропривод | 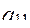
| 0,80 | 100 | 100 |
| Механический редуктор | 
| 0,85 | 180 | 100 | ||
| ИМ |
| Гидравлический домкрат | 
| 0,80 | 160 | 70 |
| Винтовой домкрат | 
| 0,85 | 120 | 90 | ||
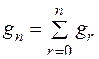
или
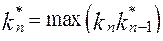
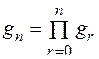
производится расчет параметров таблицы динамического программирования (табл. 20).
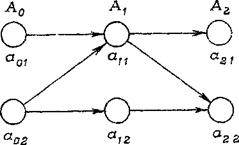
Рис. 93. Морфологический граф
Анализ данных таблицы ДП показывает, что на втором шаге вариант 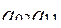 может быть отброшен, так как по значениям критерия
может быть отброшен, так как по значениям критерия 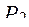 и ограничений
и ограничений 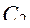 он хуже варианта
он хуже варианта 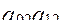 . Кроме того, данные этой таблицы свидетельствуют о том, что хотя вариант
. Кроме того, данные этой таблицы свидетельствуют о том, что хотя вариант 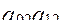
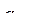 имеет наибольшую вероятность безотказной работы (Р = 0,593), но, в то же время, он не удовлетворяет ограничению по стоимости. Поэтому лучшим является вариант
имеет наибольшую вероятность безотказной работы (Р = 0,593), но, в то же время, он не удовлетворяет ограничению по стоимости. Поэтому лучшим является вариант 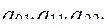 так как он имеет наибольшее значение критерия (
так как он имеет наибольшее значение критерия ( 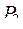 =0,563) и удовлетворяет принятым ограничениям (
=0,563) и удовлетворяет принятым ограничениям ( 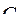 =270 у. ед.,
=270 у. ед., 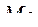 =230 у. ед.). Таким образом, в рассмотренном примере в оптимальную структуру электропривода входят электродвигатель первого типа
=230 у. ед.). Таким образом, в рассмотренном примере в оптимальную структуру электропривода входят электродвигатель первого типа 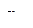 , гидравлический передаточный механизм
, гидравлический передаточный механизм 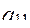 и винтовой домкрат
и винтовой домкрат 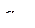 .
.
Таблица 20
Расчетная таблица
Обозначение элементов морфологического графа и значения 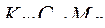
| Шаг №1 | Шаг № 2 | Шаг № 3 | |||
|
| 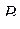 = 0,83 = 0,83
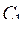 = 50 = 50
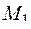 = 50 = 50
|
| 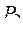 = 0,664 = 0,664
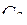 =150 =150
 =150 =150
| 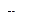
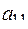
| 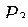 = 0,532 = 0,532
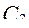 = 250 = 250
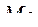 =220 =220
|
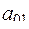
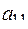
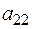
| 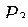 = 0,563 = 0,563
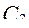 =270 =270
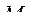 = 230 = 230
| ||||
|
| 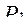 = 0,82 = 0,82
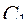 = 60 = 60
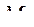 = 100 = 100
| 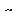
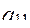
| 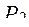 =0,656 =0,656
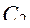 =250 =250
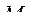 =200 =200
| - | - |
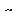
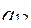
| 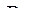 =0,697 =0,697
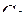 =230 =230
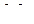 =200 =200
| 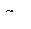
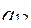
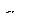
| 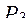 =0,593 =0,593
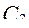 = 350 = 350
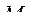 =280 =280
| ||
Примечание. Зависимости для 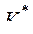 могут иметь и другие ограничения. Например, в рассматриваемом примере использовалась целевая функция и ограничение
могут иметь и другие ограничения. Например, в рассматриваемом примере использовалась целевая функция и ограничение
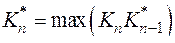
и ограничение
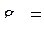
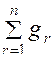 .
.
Вычислительные процедуры и алгоритмы решения задач структурного синтеза методами ДП (как это следует на приведенного выше примера) и ветвей и границ (как его следует из опыта его применения, см. рекомендованную литературу) существенно усложняются при введении большого числа ограничений. В определенной степени этого недостатка лиши метод последовательного анализа и отсева вариантов, что существенно усиливает практическую значимость его.
Рассмотрим сначала методику решения однокритериальной задачи структурного синтеза объекта проектирования, которая может быть положена в основу решения многокритериальных задач (как в случае применения метода ДП). Исходными данными является морфологическая таблица, на основе, которой строится матрица вида
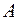 =
= 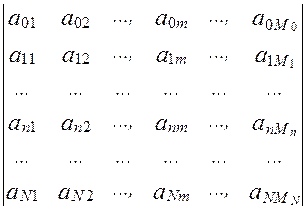 . (43)
. (43)
Решение задачи начинается с выявления и отсева вариантов технической реализации подсистем исходя из заданных ограничений. Для этого производится упорядочение матрицы (42) для каждого ограничения таким образом, чтобы значения функций ограничения для каждого варианта технической реализации n-й подсистемы 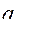 в упорядоченной матрице
в упорядоченной матрице 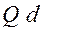 располагались от минимального до максимального значения при ограничении сверху (меньше) или в обратном порядке при ограничении снизу (больше)
располагались от минимального до максимального значения при ограничении сверху (меньше) или в обратном порядке при ограничении снизу (больше)
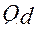 =
= 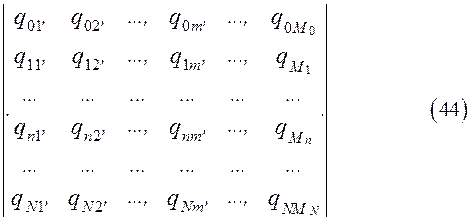
Затем путем суммирования или перемножения (в зависимости от вида функций ограничений) элементов первых столбцов матрицы 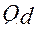 определяется минимальные
определяется минимальные 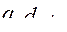 , или максимальные
, или максимальные 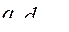 значения функций ограничений. Если
значения функций ограничений. Если 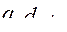 больше или
больше или 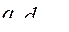 меньше допустимого значения для d-го ограничения
меньше допустимого значения для d-го ограничения 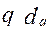 ,то объект из рассматриваемых вариантов подсистем не может быть синтезирован и задача не имеет решения.
,то объект из рассматриваемых вариантов подсистем не может быть синтезирован и задача не имеет решения.
Далее для каждой из строк матрицы 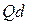 . вычисляются допуски
. вычисляются допуски 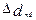 на основе следующих зависимостей.
на основе следующих зависимостей.
Для аддитивных ограничений:
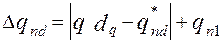 (45)
(45)
Для мультипликативных ограничений:
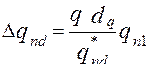 , (46)
, (46)
где 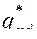 - максимальное
- максимальное 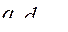 или минимальное
или минимальное 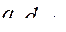 значение функций
значение функций
ограничений;
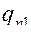 - n-й элемент первого столбца матрицы
- n-й элемент первого столбца матрицы 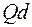 .
.
Отброс бесперспективных вариантов технической реализации подсистем осуществляется в случаях:
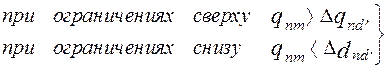 , (47)
, (47)
при ограничениях сверху при ограничениях снизу
После отброса бесперспективных вариантов подсистем по первой матрице ограничений производится корректировка исходной морфологической матрицы 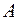 и остальных матриц ограничений. Таких циклов отбрасывания бесперспективных вариантов подсистем может быть проведено несколько, после чего оставшиеся варианты включаются в новую матрицу
и остальных матриц ограничений. Таких циклов отбрасывания бесперспективных вариантов подсистем может быть проведено несколько, после чего оставшиеся варианты включаются в новую матрицу 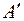 . Если в матрице еще остается значительное количество элементов, при котором простым перебором выявить оптимальную структуру объекта (РК или РСЗО) затруднительно, производится отсев вариантов реализации подсистем по критерию. Для этого на основе матрицы
. Если в матрице еще остается значительное количество элементов, при котором простым перебором выявить оптимальную структуру объекта (РК или РСЗО) затруднительно, производится отсев вариантов реализации подсистем по критерию. Для этого на основе матрицы 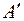 строится упорядоченная матрица
строится упорядоченная матрица 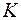 , в которой при максимизации критерия элементы размещаются в порядке убывания значений критерия
, в которой при максимизации критерия элементы размещаются в порядке убывания значений критерия 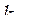
Суммированием или перемножением (в зависимости от математической формы критерия) элементов первого столбца матрицы 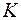 определяется максимальное значение критерия
определяется максимальное значение критерия 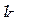 . Назначается допустимое значение критерия
. Назначается допустимое значение критерия 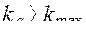 . Затем по матрице
. Затем по матрице 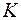 производится отсев бесперспективных вариантов подсистем, так же, как и по матрицам ограничений. После корректировки матрицы
производится отсев бесперспективных вариантов подсистем, так же, как и по матрицам ограничений. После корректировки матрицы 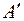 циклы отсева вариантов на основе рассмотренной методики могут повторяться до тех пор, пока не прекратится отсев вариантов и в матрице
циклы отсева вариантов на основе рассмотренной методики могут повторяться до тех пор, пока не прекратится отсев вариантов и в матрице 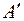 ' не останется один или небольшое количество вариантов возможных структур РК или РСЗО, т.е. пока не станет возможным выбор оптимальной структуры путем элементарного перебора.
' не останется один или небольшое количество вариантов возможных структур РК или РСЗО, т.е. пока не станет возможным выбор оптимальной структуры путем элементарного перебора.
Рассмотрим по данному вопросу конкретный пример.
Пусть требуется определить оптимальную структуру гидравлического привода для перспективной боевой машины РСЗО, который состоит из электрического источника энергии 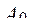 , гидронасоса
, гидронасоса 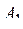 , регулирующей аппаратуры
, регулирующей аппаратуры 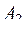 и исполнительного элемента
и исполнительного элемента 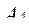 , при условии обеспечения максимальной вероятности безотказной работы привода
, при условии обеспечения максимальной вероятности безотказной работы привода 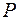 и ограничений по стоимости
и ограничений по стоимости 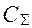 , массе
, массе 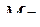 и объему
и объему 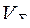 , т.е. математически это можно выразить следующим образом
, т.е. математически это можно выразить следующим образом
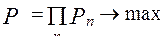 ;
;
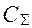 =
= 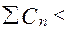 50 у.ед.;
50 у.ед.;
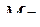 =
= 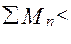 65 у.ед.;
65 у.ед.;
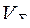 =
= 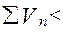 65 у.ед..
65 у.ед..
Исходная морфологическая матрица, матрицы критерия и ограничений (в условных единицах) имеют вид
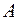 =
= 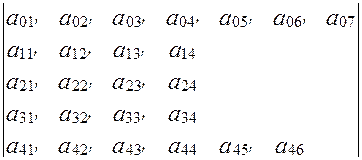 ,
,
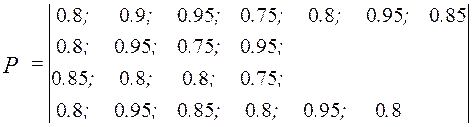 ,
,
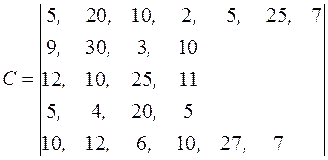 ,
,
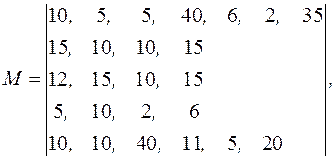
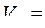
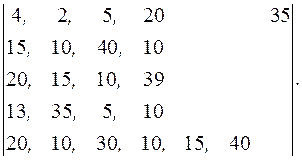
Решение задачи целесообразно начать с отсева бесперспективных вариантов по матрицам ограничений. Для этого упорядочим матрицу ограничений по стоимости (по мере возрастания численных значений)
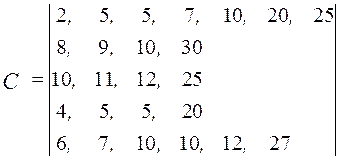 ,
,
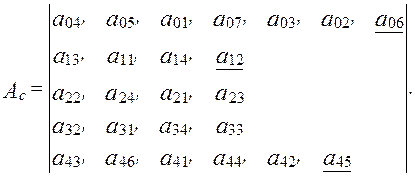
Сложив элементы первого столбца матрицы 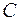 , определим
, определим 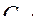 =30, что меньше допустимого значения. Следовательно, задача по ограничению стоимости имеет допустимое решение. По зависимости (44), на которой останавливались выше, найдем допуски
=30, что меньше допустимого значения. Следовательно, задача по ограничению стоимости имеет допустимое решение. По зависимости (44), на которой останавливались выше, найдем допуски
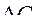 :
: 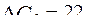 ;
; 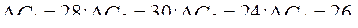
Исходя из условия (46) при ограничении сверху, проверяем допустимость использования в системе элементов матрицы  . Очевидно, что варианты технической реализации подсистем
. Очевидно, что варианты технической реализации подсистем 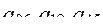 должны быть отброшены.
должны быть отброшены.
С учетом отброшенных вариантов подсистем строим упорядоченную матрицу ограничений по массе.
Отсев вариантов по матрице 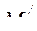 не производится.
не производится.
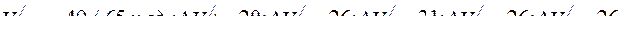 .
.
Также не производится отсев вариантов по матрице 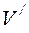 . Применение процедуры отсева вариантов по матрицам ограничений в третий раз не приводит к дальнейшему сокращению матрицы
. Применение процедуры отсева вариантов по матрицам ограничений в третий раз не приводит к дальнейшему сокращению матрицы 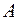 .
.
После всех отсевов вариантов морфологическая матрица будет иметь вид
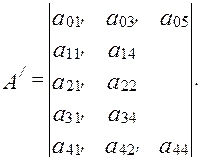
Таким образом, число всевозможных вариантов структуры гидравлического привода сократилось с 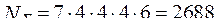 до
до 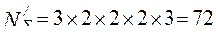 . Однако количество возможных вариантов структуры остается еще достаточно значительным. Поэтому целесообразно далее применить процедуру отсева вариантов подсистем по критерию
. Однако количество возможных вариантов структуры остается еще достаточно значительным. Поэтому целесообразно далее применить процедуру отсева вариантов подсистем по критерию 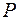 . Для этого необходимо построить упорядоченную матрицу по критерию
. Для этого необходимо построить упорядоченную матрицу по критерию 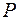 (по мере убывания значений критерия)
(по мере убывания значений критерия)
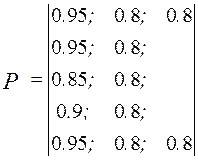
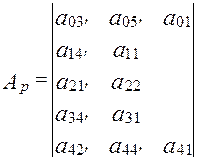 .
.
Следовательно,  0,66.
0,66.
Проверим, удовлетворяет ли ограничениям по стоимости, массе и объему привод, состоящий из элементов первого столбца матрицы 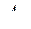 . Имеем
. Имеем 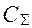 =49<50 у.ед.,
=49<50 у.ед., 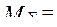 48<65 у.ед.,
48<65 у.ед., 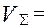 55<65 у.ед. Таким образом, оптимальной является структура привода, состоявшая из подсистем
55<65 у.ед. Таким образом, оптимальной является структура привода, состоявшая из подсистем  и
и  . Она имеет максимально возможную вероятность безотказной работы (
. Она имеет максимально возможную вероятность безотказной работы ( 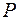 =0,66) и удовлетворяет всем заданным ограничениям.
=0,66) и удовлетворяет всем заданным ограничениям.
Рассмотренный метод скалярной оптимизации может быть применен при решении многокритериальных задач структурного синтеза для выделения множества эффективных альтернатив и поиска среди них лучшего варианта структуры (с точки зрения ЛПР).
Идеи метода последовательного анализа и отсева вариантов могут быть использованы для непосредственного решения многокритериальной задачи. При этом общая процедура ее решения аналогична рассмотренной. Отличие заключается в том, что после отсева вариантов подсистем по матрицам ограничений производится еще их отсев на основе анализа упорядоченных матриц критериев 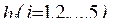 , в который элементы размещаются в порядке убывания при максимизации критериев и в порядке возрастания при их минимизации. По значениям элементов первых столбцов матрицы
, в который элементы размещаются в порядке убывания при максимизации критериев и в порядке возрастания при их минимизации. По значениям элементов первых столбцов матрицы 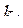 определяются максимальные или минимальные значения критериев. Затем на каждый критерий назначаются допустимые значения (с точки зрения ЛПР) отклонения их от оптимальных значений. При этом методика отсева бесперспективных вариантов по матрицам критериев такая же, как и по матрицам ограничений.
определяются максимальные или минимальные значения критериев. Затем на каждый критерий назначаются допустимые значения (с точки зрения ЛПР) отклонения их от оптимальных значений. При этом методика отсева бесперспективных вариантов по матрицам критериев такая же, как и по матрицам ограничений.
Дата: 2019-02-02, просмотров: 815.