Не полностью определенных логических функций – это функции, для которых не на всех возможных наборах комбинаций входных сигналов в таблице истинности определены значения выходного сигнала. Эта ситуация возможна как для комбинационных, так и для последовательных логических функций. При заполнении таблицы истинности на неопределенных наборах логической функции вместо значений выходного сигнала ставится прочерк.
Алгоритмы логического управления описываются в основном не полностью определенными логическими функциями, поскольку ряд комбинаций значений входных сигналов неосуществим физически для реального технологического процесса.
При построении схемы логического управления на неопределенных наборах функции ее значение выходного сигнала является безразличным и может принимать одно из двух значений - 0 или 1.
Минимизация и анализ всех вариантов реализации неопределенной логической функции с целью выбора самого оптимального из них является громоздкой задачей. Поэтому для получения лишь одного варианта реализации следует учитывать особенности технологического процесса.
Пример. В бак (рис.3.8) поступает случайный во времени поток воды Q. От электродных датчиков уровня НУ и ВУ поступают дискретные сигналы при достижении водой заданного уровня их установки. Насос Н должен включаться при достижении водой верхнего уровня – ВУ; насос Н должен отключиться при опорожнении бака и исчезновении сигнала от датчика нижнего уровня – НУ. Логическая схема управления содержит два входных сигнала НУ и ВУ и один выходной сигнал Н.
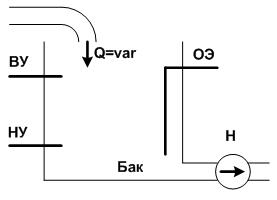
Рис. 3.8. Технологическая схема подачи воды при опорожнении бака: Н – насос; ОЭ – общий электрод; НУ – нижний уровень; ВУ - верхний уровень; Q = var – случайный расход воды.
Вводим условные обозначения:
0 – отсутствие сигнала;
1 – наличие сигнала;
НУ и ВУ – сигналы на входе, т.е. от датчиков нижнего и верхнего уровня;
Н – сигнал на выходе, т.е. управления электродвигателем насоса.
Составляем логические высказывания:
исходное состояние НУ=0 И ВУ=0 – Н=0; при НУ=1 И ВУ=0 – Н=0; при НУ=1 И ВУ=1 – Н=1; при НУ=1 И ВУ=0 – Н=1; при НУ=0 И ВУ=0 – Н=0.
Построим диаграмму тактов для технологической схемы подачи воды при опорожнении бака (рис. 3.8) – рис. 3.9.
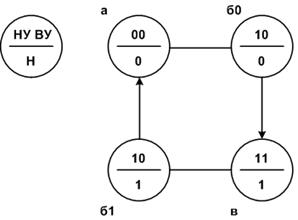
Рис. 3.9. Диаграммы тактов к примеру
Диаграмма тактов, приведенная на рис. 3.9, содержит два неоднозначных такта: б0, б1; они свидетельствуют о наличии контуров обратной связи, т.е. это последовательная логическая функция.
Таблица истинности, составленная согласно логическим высказываниям и диаграмме тактов, представлена в таблице 3.5; в ней на наборе 2 наличие неоднозначных тактов отражено символами 0,1.
Как следует из таблицы 2.9, эта функция является не полностью определенной, т.к. на наборе номер 1 значение ее выходного сигнала не задано.
Согласно описанию технологического процесса подачи воды при опорожнении бака в нормальном режиме работы комбинация входных сигналов НУ=0 И ВУ=1 является невозможной.
Таблица 3.5 – Таблица истинности для схемы подачи воды
| № | НУ | ВУ | Н | На |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | — | 1 |
| 2 | 1 | 0 | 0, 1 | 0, 1 |
| 3 | 1 | 1 | 1 | 1 |
Для обеспечения правильной работы оборудования во внештатных ситуациях следует на неопределенном такте – 1 присвоить выходному сигналу значение Н=1. В этом случае при комбинации входных сигналов НУ=0 И ВУ=1 (она возможна при обрыве сигнальной цепи датчика НУ) переполнения бака поступающей водой не произойдет. Следовательно, в таблицу 3.5 с учетом этого допущения добавим столбец – На.
ДНФ для заданной в таблице 3.5 логической функции имеет вид:
На= Y 1 · На+ Y 2,
где Y 1 – ДНФ при выходном сигнале, равном 1 на неоднозначных тактах; Y 2 – ДНФ при выходном сигнале, равном 0 на неоднозначных тактах. Для рассматриваемого примера получим:
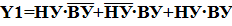
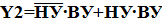
Минимизацию выполним методом непосредственного упрощения для Y 1, Y 2, т.е.
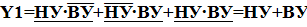
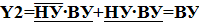
Алгоритм управления насосом при опорожнении бака примет вид:
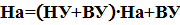
В случае, если особенности технологического процесса не существенны, то минимизацию не полностью определенных логических с целью уменьшения числа рассматриваемых вариантов рекомендуется выполнять в следующей последовательности:
- в таблице истинности на всех неопределенных наборах выходным сигналам логической функции присваивают значение логического 0, получается полностью определенная дополнительная таблица истинности;
- проводят минимизацию дополнительной таблицы истинности, используя ее аналитическую запись в виде ДНФ методом непосредственного упрощения или другими методами.
В заключение отметим, что при синтезе систем логического управления необходимо стремиться представить её состоящей из конечного числа более простых логических схем, имеющих только один выходной сигнал. В этом случае синтез устройства управления может быть значительно упрощён. На первом этапе выполняют синтез более простых схем. На втором этапе полученные в результате синтеза отдельные схемы объединяют в одну схему, которая реализует заданный алгоритм управления.
ПРИЛОЖЕНИЕ.
Дата: 2019-02-02, просмотров: 743.