Логические системы управления делятся на следующие виды:
комбинационные – значения выходного сигнала зависят только от комбинаций значений входных сигналов, т.е. они полностью определены на всех возможных наборах таблицы истинности, во всех выше рассмотренных примерах использовались комбинационные логические функции;
последовательные – значения выходного сигнала зависит как от комбинаций значений входных сигналов, так и от предыдущего состояния системы. Эти устройства содержат память, которая запоминает предыдущее состояние системы.
Последовательные логические функции задаются и минимизируются теми же способами, что и комбинационные логические функции, но с учетом их специфических особенностей.
При синтезе последовательной логической схемы для понимания её работы удобно пользоваться диаграммой состояний логической схемы.
Диаграмма состояний представляет собой графическое описание условий работы логических схем, имеющих, как правило, один выходной сигнал. Они отражают взаимосвязи входных и выходных сигналов, условия и порядок их изменения.
Диаграмма состояний является наглядной и удобной формой записи алгоритмов логического управления
На диаграммах состояний применяют следующие условные обозначения и ограничения:
- каждое состояние схемы обозначается кружочком;
- состояние входных сигналов и выходного сигнала для любого состояния записывается в виде дроби, имеющей в числителе запись в строго оговоренной последовательности комбинацию значений входных сигналов, а в знаменателе – значение выходного сигнала;
- соседними состояниями являются лишь те состояния, которые отличаются значением только одного сигнала;
- графические связи могут быть показаны только между соседними состояниями;
- графические связи изображаются прямыми линиями со стрелкой или без нее; линии без стрелки разрешают переходы между состояниями в обоих направлениях при изменении значения одного из входных сигналов; линии со стрелкой разрешают переход с состояния на состояние только по направлению стрелки;
- состояния, имеющие различные комбинации значений входных сигналов, обозначаются различными буквами;
- состояния, имеющие одинаковые комбинации значений входных сигналов, но разные значения выходного сигнала, обозначаются одной и той же буквой, имеющей индексы 0 или 1, соответствующие значению выходного сигнала;
-условия порядка записи комбинаций входных сигналов задаются в виде отдельного такта, находящегося на свободном месте диаграммы.
Пример. Диаграмма тактов для логического элемента И показана на рис. 3.6.
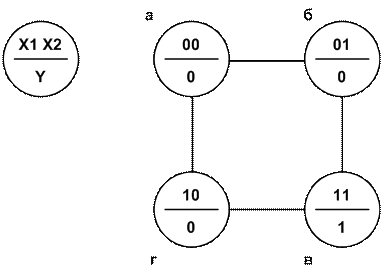
Рис. 3.6. Диаграмма тактов логического элемента И.
Рассмотрим на примере методику синтеза последовательной схемы для случая, когда значения выходного сигнала последовательной функции зависят как от комбинации значений входных сигналов в данный момент времени, так от значения выходного сигнала в предшествующий момент времени. Эта зависимость реализуется в виде сигнала обратной связи, подаваемого с выхода схемы на ее вход.
Пример: Управление вытяжными вентиляторами.
В логической системе управления температурой воздуха в помещении установлены два датчика температуры с разными уставками срабатывания Т1 и Т2, причем Т1 ≠ Т2. Эти датчики имеют одинаковую конструкцию и дискретный выходной сигнал. Если температура в месте расположения датчика меньше его уставки, то выходной сигнал равен 0. Если температура равна или больше уставки датчика, то выходной сигнал равен 1. Эти сигналы поступают на вход логической схемы управления вытяжными вентиляторами.
Словесный алгоритм управления работой вентиляторов:
в исходном состоянии сигналы датчиков Т1 и Т2 отсутствуют и вентиляторы отключены; вентиляторы включаются только тогда, когда есть сигналы от обоих датчиков Т1 и Т2; вентиляторы работают до тех пор, пока не исчезнут сигналы от обоих датчиков Т1 и Т2; все входные и выходные сигналы являются дискретными и изменяются в произвольные моменты времени, одновременного изменения значений сигналов Т1 и Т2 быть не может; аварийные и нештатные ситуации не рассматриваются, сигналы блокировок и защиты не учитываются.
Вводим условные обозначения:
Т1 и Т2 – два входных сигнала от датчиков температуры;
Д – выходной сигнал, который управляет включением и отключением электродвигателей вентиляторов;
0 – отсутствие сигнала;
1 – наличие сигнала.
Составляем логические высказывания:
исходное состояние Т1=0 И Т2=0 – Д=0; если Т1=0 И Т2=1 ИЛИ Т1=1 И Т2=0, то Д=0; если Т1=1 И Т2=1, то Д=1; если Т1=0 И Т2=1 ИЛИ Т1=1 И Т2=0, то Д=1; при Т1=0 И Т2=0 – Д=0.
Построим диаграмму состояний согласно заданным словесному алгоритму и логическим высказываниям – рис. 3.7.
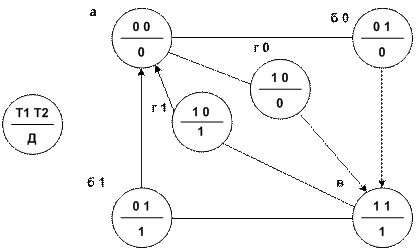
Рис. 3.7. Диаграмма состояний схемы управления вентиляторами.
Диаграмма тактов, приведенная на рис. 3.7, содержит четыре неоднозначных такта: б0, б1 и г0, г1; они свидетельствуют о наличии контуров обратной связи, т.е. это последовательная логическая функция.
Таблица истинности, составленная согласно логическим высказываниям и диаграмме состояний, представлена в таблице 3.4; в ней на наборах 1 и 2 наличие неоднозначных состояний отражено символами 0,1.
Таблица 3.4 – Таблица истинности управления вытяжным вентилятором.
| № | Т1 | Т2 | Д |
| 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0,1 |
| 2 | 1 | 0 | 0,1 |
| 3 | 1 | 1 | 1 |
Минимизация последовательных логических функций проводится аналогично и теми же методами, как и для комбинационных логических функций. Однако, при этом следует выполнить минимизацию двух вспомогательных функций Y 1 и Y 2, где Y 1 – ДНФ при выходном сигнале, равном 1 на неоднозначных тактах; Y 2 – ДНФ при выходном сигнале, равном 0 на неоднозначных тактах. В этом случае ДНФ для заданной последовательной логической функции Y имеет вид:
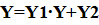 ,
,
Для рассматриваемого примера получим:
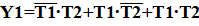
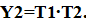
Минимизацию Y 1 и Y 2 выполним методом непосредственного упрощения, в данном примере ее требуется провести только для Y 1, т.е. 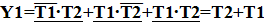
ДНФ для заданной в таблице 3.4 логической функции имеет вид:
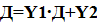 ,
,
Алгоритм управления вентиляторами примет вид:
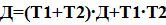 .
.
Дата: 2019-02-02, просмотров: 377.