Упрощение логических формул позволяет свести к минимуму число логических элементов, необходимых для реализации логической функции. Для минимизации формул используются законы и тождества математической логики. Однако в общем случае непосредственное применение законов и тождеств математической логики для преобразований логических формул приводит к громоздким выкладкам и связано с большой затратой времени. При этом трудно бывает оценить, является ли полученное выражение простейшим или возможны дальнейшие упрощения. Поэтому в математической логике разработан ряд приемов, которые позволяют упрощать логические формулы более просто, быстро и безошибочно. Если число входных переменных не превышает четырех, то нахождение простейших видов логических формул удобно производить с помощью метода карт Карно.

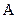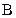Карты Карно с двумя переменными. Карта Карно для двух переменных показана на рис. 7.4, а. Четыре квадрата (1, 2, 3, 4) соответствуют четырем возможным комбинациям  и  в таблице истинности с двумя переменными. Квадрат 1 соответствует произведению 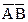, квадрат 2 — произведению  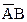и т.д.

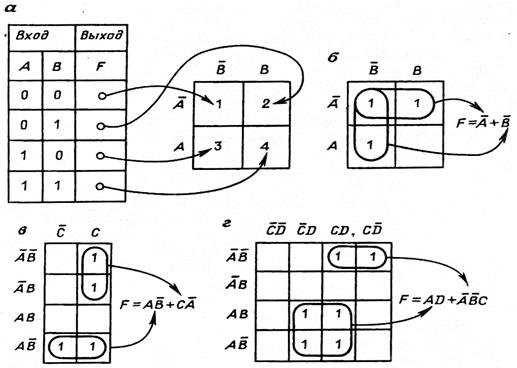
Рис. 3.4. Карты Карно

Составим карту Карно для логического выражения 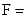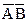+ + 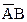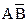. Карта Карно для этого случая показана на рис. 3 4, б. Разместим логические единицы во всех квадратах, которым соот­ветствуют произведения в исходном логическом выражении. Объединим соседние единицы в один контур группами по две, че­тыре или восемь единиц. Контуры строим до тех пор, пока все единицы не окажутся внутри контуров. Каждому контуру соот­ветствует одно слагаемое упрощенного логического выражения, записанного в дизъюнктивной нормальной форме. На рис. 3.4, б у нас получилось два контура. Следовательно, упрощенное выражение будет состоять из двух слагаемых. Получим это выражение. Возьмем верхний контур. 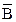Здесь переменная  встречается в комбинации с  и 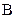. В соответствии с правилами булевой алгебры 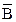+ 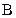=1. Поэтому  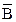и 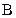 здесь опускаются. Тогда в верхнем контуре остается переменная . 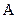Вертикально расположенный контур содержит  и  Так как + 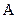=1, то  и 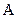 также опускаются, остается только 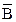. Оставшиеся в результате  и 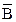 затем объединяются посредством операции логического сложения, что приводит к упрощенному логическому выражению = + .

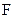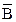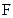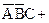
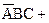
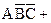
Карты Карно с тремя переменными. Пусть дано логическое выражение = 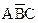. Упростим его с помощью карты Карно. Для случая трех переменных карта Карно содер­жит восемь квадратов (рис. 3.4, в). Каждый квадрат соответствует одной из возможных комбинаций переменных 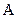,  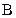и 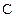. Занесем в квадраты, которые отображают каждое из слагаемых исходного логического выражения, четыре единицы. Возьмем нижний контур. Здесь произведение  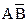встречается в комбинации с  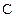и . 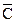Так как 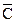+ 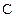=1, то  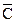и 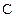 можно опустить. Поэтому остается произведение 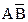. В верхнем контуре переменная  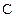встречается в комбинаци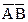и  и 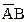. Так как 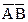+ 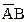= , то в результате остается произведение 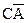. Полученные произведения объединяются посредством операции логического сложения, и мы получаем упрощенное логическое выражение в ДНФ.

= + .

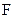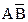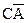Карты Карно с четырьмя переменными. Составим карту Карно для логического выражения

.

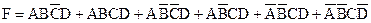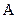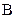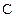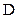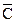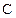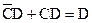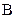Карта Карно с четырьмя переменными (рис. 6.4, г) допускает 16 возможных комбинаций , ,  и . Этим комбинациям соответствуют 16 квадратов. Нанесем на карту шесть единиц, которые соответствуют шести слагаемым в данном выражении. Группы из двух и четырех единиц объединены квадратами. В нижнем контуре из четырех единиц опускаются  и , так как , и  и 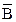, так как 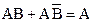. Поэтому нижний контур содержит слагаемое 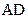. В верхнем контуре переменная  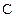встре­чается в комбинаци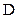и  и 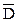, которые можно опустить. После это­го верхний контур будет содержать слагаемое 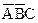. Полученные произведения объединяются посредством операции логического сло­жения, и Mid получаем упрощенное логическое выражение в ДНФ:

= + .

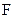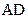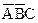Для упрощения логических выражений в рассмотренных случаях применялась одинаковая процедура, которая состоит из следующих операций.

1. Записываем исходное логическое выражение в ДНФ.

2. Заполняем карту Карно. Каждый квадрат при наличии в полученном выражении соответствующих комбинаций входных переменных обозначаем цифрой 1.

3. Соседние единицы соединяем в один контур группами по две, четыре или восемь единиц. Построение контуров продолжается до тех пор, пока все единицы не окажутся внутри контуров. Контуры могут накладываться друг на друга. Для успешного упрощения логического выражения на карте Карно нужно расположить минимальное число контуров, каждый из которых содержит наибольшее число квадратов.

4. Каждый контур представляется в виде логического произведения. Если соседние квадраты в контуре соответствуют прямому и инверсному значениям какой-либо переменной, то эта переменная в данном произведении опускается.

5. Получившиеся для каждого контура логические произведения записываем в виде логической суммы. Это будет результат упрощения исходного логического выражения.

После минимизации логической формулы необходимо составить логическую схему. Для этого необходимо использовать логические элементы ИЛИ, И, НЕ, ИЛИ — НЕ, И — НЕ и дру­гие, выпускаемые промышленностью.

Пример. Требуется создать логическое устройство для управления вентилятором. Вентилятор может быть включен непосредственно (A = 1) или по команде с диспетчерского пункта (B = 1). Вентилятор работает только тогда, когда ток его электродвигателя меньше допустимого значения (логическая функция С = 0). Разобьем решение задачи на несколько этапов.

Этап 1. Составление таблицы истинности (табл. 3.3). В соответствии с условиями задачи заполняем таблицу истинности, в которой записываем значения логической формулы вентилятора F в зависимости от входных логических переменных А, В, С для всех возможных вариантов их сочетаний. При трех входных переменных число таких сочетаний равно 8.

Таблица 3.3

Таблица истинности логического устройства

Этап 2. Получение логической формулы. Выделим в таблице истинности строки 2, 4 и 6. Запишем для каждой из выделенных строк формулу для логического умножения переменных A, В и С или их отрицаний. Причем переменные, имеющие в выделенной строке значение 0, берутся со знаком отрицания, а переменные, имеющие значение 1, — без отрицания. В результате получим следующие формулы логического умножения 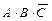для 2-й строки,  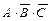для 4-й строки,  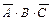для 6-й строки. Искомой формулой  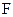будет являться логическая сумма полученных произведений:

+ + .

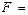
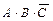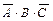Этап 3. Минимизация формулы. Можно создать логическое устройство, которое непосредственно реализует эту формулу. Тогда для выполнения инверсий 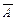, , 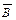 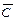потребуется три элемента НЕ, для выполнения логического умножения необходимо три трехвходовых элемента И и для выполнения логического сложения необходим трехвходовый элемент ИЛИ. Всего необходимо использовать семь элементов.

Однако полученную формулу можно упростить. Для этого воспользуемся тождеством 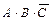 = 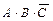+  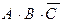и вынесем за скобки общие члены:

+ + + = .

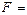
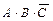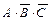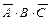Так как 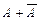=1 и 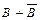=1, то .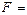

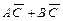
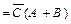Таким образом, воспользовавшись тождествами алгебры логики, мы упростили исходную логическую формулу.

Минимизацию формулы 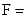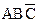+ + 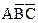 можно провести также с помощью карты Карно для трех переменных (рис. 3.5, а). Разместим логические единицы во всех квадратах, которым соответствуют произведения в исходном логическом выражении. Объединим соседние единицы в два вертикальных контура.

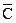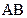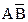Возьмем нижний вертикальный контур. Здесь переменная  встречается в комбинации с  и . Следовательно, в результате останется произведение 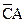. В верхнем контуре переменная  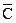встречается в комбинации с  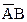и . Следовательно, в результате останется произведение 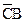. Полученные произведения объединяются посредством операции логического сложения, и мы получаем упрощенное логическое выражение в ДНФ

+ ,

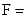
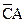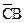
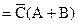что совпадает с полученной ранее формулой.

Этап 4. Построение логической схемы. Минимизированная формула содержит три операции: логическое сложение, логическое умножение, логическое отрицание. В соответствии с этим схема логического устройства, приведённая на рис. 3.5, б, выполнена на логических элементах ИЛИ, И, НЕ.

Выходной логический сигнал F поступает далее на вход системы управления электродвигателя вентилятора и включает его при F=1 или отключает при F=0.

На данном примере мы убедились, какие возможности дает алгебра логики для синтеза логических схем. Порядок решения задачи, разбиваемый на четыре этапа, сохраняется, если разрабатываются и более сложные комбинационные схемы.

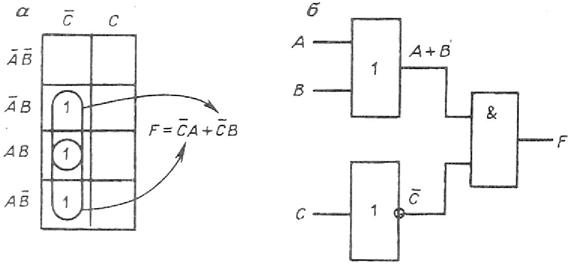
Рис. 3.5. Схема реализации логического устройства управления