Комбинационной логической схемой называется схема, в которой выходной сигнал определяется только соответствующей комбинацией сигналов на входе устройства. В них нет запоминающих устройств.
Синтез комбинационных логических схем заключается в следующем. По требуемому алгоритму работы управляющего устройства находится логическая формула, которая связывает управляющее воздействие (выходной сигнал) с входными сигналами (логическими переменными). Далее, по известным правилам алгебры логики полученную логическую формулу необходимо минимизировать, т.е. получить ее более простое выражение. На основании минимизированного выражения синтезируют логическую схему. Так как при синтезе используется упрощенная формула, то это позволяет построить логическую схему с минимальным содержанием в ней логических элементов, что уменьшает ее стоимость и повышает надежность работы.
ПОСТРОЕНИЕ КОМБИНАЦИОННЫХ СХЕМ НА ОСНОВЕ ЛОГИЧЕСКИХ ФОРМУЛ.
Логическая формула может быть записана аналитически различными сочетаниями операций логического сложения и умножения переменных. Однако с точки зрения удобства записи логической формулы и последующего синтеза логической схемы наиболее удобны формы записи, при которых формула выражается либо в виде суммы произведений переменных, либо в виде произведения их сумм.
Запись логической формулы в виде суммы произведений переменных называют дизъюнктивной нормальной формой (ДНФ) данной формулы:
.
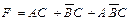Запись логической формулы в виде произведения суммы переменных называют конъюнктивной нормальной формой (КНФ) данной формулы:
.
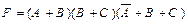Пользуясь законами и тождествами математической логики, всякую формулу, заданную любым аналитическим выражением, можно преобразовать в равносильную ей формулу в виде ДНФ или КНФ. Для каждой логической формулы может существовать несколько равносильных дизъюнктивных и конъюнктивных форм.
 |
Пример. Построить логическую схему для логической формулы
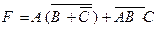, предварительно преобразовав ее в ДНФ.
Рис.3.1. Этапы построения схемы для логического выражения в ДНФ
Применим к данной формуле законы Де Моргана:
.
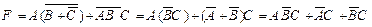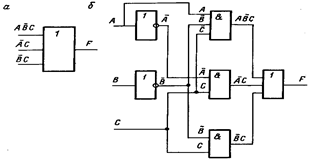
Мы получили запись исходного выражения в ДНФ. Построим логическую схему, которая реализует эту функцию. На рис. 3.1, а показан первый этап построения этой схемы. Для получения нужного результата на выходе схемы F отдельные слагаемые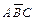 
, 
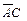и 
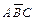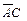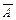должны быть связаны между собой логическим элементом ИЛИ. На рис. 5.1, б показан второй этап построения логической схемы. Для получения выражений , и в схему добавлены логические элементы И, а для получения на входе элементов И инверсных значений 
и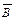 
используются инверторы. Выходные сигналы с элементов И поступают на вход элемента ИЛИ. Схема, приведенная на рис. 5.1, б, представляет собой логическую схему, которая реализует исходное логическое выражение 
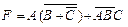, записанное в ДНФ.
Пример. Построить логическую схему для логического выражения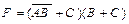 
, предварительно преобразовав его в конъюнктивную нормальную формулу.
Применим к данной формуле законы Де Моргана
.
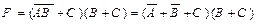Мы получили запись исходного выражения в КНФ. Построим логическую схему, которая реализует эту функцию. Первый этап построения схемы показан на рис. 3.2, а. Для получения нужного результата F на выходе схемы множители этого выражения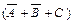 
и 
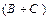должны быть связаны функцией И. На рис. 3.2, б показан второй этап построения логической схемы. Для получения выражени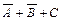й 
и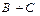 
в схему добавлены логические элементы ИЛИ, а для получения на входе элементов ИЛИ инверсных значени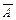й и 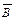используются инверторы. Выходные сигналы с элементов ИЛИ поступают на вход элемента И.
Приведенная на рис. 3.2, б схема реализует исходное логическое выражение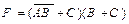 
, записанное в КНФ.
 |
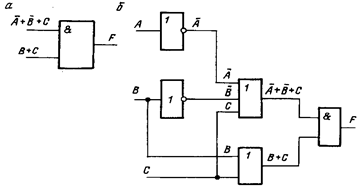Рис.3.2. Этапы построения схемы для логического выражения в КНФ
Необходимо отметить, что при составлении комбинационных логических схем мы использовали только логические элементы И, ИЛИ, НЕ.
Анализируя процесс построения логических схем на основе логических элементов, можно сделать следующие выводы:
1. Перед построением схемы исходное логическое выражение преобразуется в ДНФ или КНФ.
2. Построение логической схемы начинается с ее выхода F. Далее, преобразуя логическое выражение в логические схемы, мы постепенно движемся от выхода к входам схемы (справа налево). В этом и заключается суть построения комбинационных логических схем на основе логических выражений.
3. Логические схемы можно построить на основе логических выражений в ДНФ или КНФ. В первом случае получаются логические схемы типа И – ИЛИ (см. рис. 5.1), а во втором – схемы типа ИЛИ – И (см. рис. 5.2).
СОСТАВЛЕНИЕ ЛОГИЧЕСКИХ ФОРМУЛ ПО ЗАДАННЫМ ТАБЛИЦАМ
ИСТИННОСТИ
Логические формулы – это удобный метод описания принципа работы логической схемы. Однако при проектировании логических схем редко удается выразить решаемые такой схемой задачи непосредственно в виде логической формулы. Обычно на первом этапе синтеза используется словесное описание решаемых схемой задач, на основании которого удается составить таблицу истинности, связывающую численные значения входных и выходных логических переменных. Поэтому необходимо уметь преобразовывать информацию в форме таблицы истинности в логические формулы. Покажем, как это можно сделать.
Пусть дана таблица истинности некоторой, неизвестной пока формулы F, содержащей переменные А, В и С (табл. 3.2).
Таблица 3.2
Таблица истинности для получения логической формулы
| Номер строки | A | B | C | F |
| 1 2 3 4 5 6 7 8 | 1 0 1 0 1 0 1 0 | 1 1 0 0 1 1 0 0 | 1 1 1 1 0 0 0 0 | 1 0 0 1 0 0 0 1 |
Выделим строки, соответствующие значениям 1 искомой формулы, – это строки 1, 4 и 8. Запишем для каждой из выделенных строк формулу для логического произведения переменных А, В и С или их отрицаний. Причем переменные, имеющие в выделенной строке значение 0, берутся со знаком отрицания, а переменные, имеющие значение 1, – без отрицания. В результате получим следующие формулы логического умножения: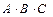 
для 1-й строки, 
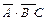для 4-й строки, 
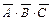для 8-й строки.
Искомой формулой F будет являться логическая сумма полученных произведений
+ + 
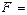
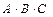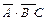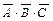. (3.1)
Подобным образом можно составить формулу для всякой таблицы истинности, в последнем столбце которой имеется хотя бы одно значение 1.
Формулу, соответствующую данной таблице, можно получить и другим способом.
Выделим те строки таблицы, в которых искомая формула принимает значение 0, – это строки 2, 3, 5, 6, 7.
Для каждой из выделенных строк составим логическую сумму переменных А, В и С или их отрицаний. Причем переменные, имеющие в выделенной строке значение 1, берутся со знаком отрицания, а переменные, имеющие значение 0, – без отрицания. В результате получим следующие формулы логического сложения: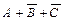 
(2-я строка), 
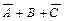(3-я строка), 
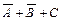(5-я строка), 
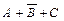(6-я строка), 
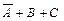(7-я строка).
Искомой формулой F будет являться логическое произведение полученных сумм:
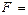
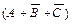
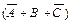
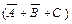
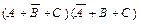. (3.2)
Как видим, первый и второй способы дают для одной и той же таблицы разные логические формулы. Однако, воспользовавшись тождествами математической логики, вторую формулу нетрудно привести к первой.
Рассмотренный метод является универсальным в том смысле, что позволяет получить логическую формулу и в соответствии с ней построить комбинационную схему для любой таблицы. Однако этот метод приводит, как правило, к сложным формулам, для реализации которых требуется большое число различных логических элементов. Поэтому важной задачей синтеза комбинационных схем является задача упрощения или минимизации логических формул.
Дата: 2019-02-02, просмотров: 329.
