В общем случае отдельное структурное уравнение системы является идентифицируемым, если имеется достаточное количество экзогенных переменных, не включенных в само уравнение, которые можно использовать как инструментальные для всех эндогенных объясняющих переменных уравнения.
В полностью определенной модели будет столько уравнений, сколько имеется эндогенных переменных.
Пусть D – число не включенных в уравнение, но присутствующих в системе экзогенных переменных, а G – число включенных в уравнение эндогенных переменных.
Необходимое условие идентификации. Уравнение в структурной модели может быть идентифицировано, если число не включенных в него экзогенных переменных не меньше числа включенных в него объясняющих эндогенных переменных, т.е.
D ³ G - 1, (порядковое условие).
Данное условие является необходимым, но не достаточным для идентификации.
В частности:
если D = G – 1, то уравнение точно идентифицируемо;
если D > G – 1, то уравнение сверхидентифицируемо;
если D < G – 1, то уравнение неидентифицируемо.
Достаточное условие идентификации. Уравнение идентифицируемо, если ранг матрицы, составленной из коэффициентов при переменных (эндогенных и экзогенных), отсутствующих в исследуемом уравнении, не меньше числа эндогенных переменных системы без единицы.
Пример 3.3. Проверим на идентификацию каждое уравнение модели:
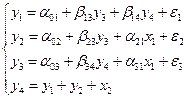
где y1 – расходы на конечное потребление данного года; y2 – валовые инвестиции в текущем году; y3 – расходы на заработную плату в текущем году; y4 – валовый доход за текущий год; x1 – валовый доход предыдущего года; x2 – государственные расходы текущего года; e – случайные ошибки.
В данной модели число эндогенных переменных N = 4 (y1, y2, y3, y4) и две экзогенных (x1, x2).
Для первого уравнения: G = 3 (y1, y3, y4 – присутствуют), D = 2 (x1, x2 – отсутствуют) и D = G – 1, поэтому уравнение точно идентифицируемо (необходимое условие). Для проверки на достаточное условие идентификации выпишем матрицу коэффициентов при переменных, не входящих в первое уравнение:
| Уравнение | y2 | x1 | x2 |
| 2 3 4 | –1 0 1 | a21 a31 0 | 0 0 1 |
Определитель матрицы detA = –a31 ¹ 0, следовательно ранг матрицы равен 3 ³ N – 1, т.е. достаточное условие идентификации выполняется, и первое уравнение точно идентифицируемо.
Второе уравнение системы также точно идентифицируемо: G = 2, D = 1 и D = G – 1. Выполняется также достаточное условие идентификации:
detA = –b34 ¹ 0, ранг матрицы равен 3 ³ N – 1
| Уравнение | y1 | y4 | x2 |
| 1 3 4 | –1 0 1 | b14 b34 –1 | 0 0 1 |
Аналогично третье уравнение системы также точно идентифицируемо: G = 2, D = 1, D = G – 1, detA = 1, ранг матрицы равен 3 ³ N – 1.
| Уравнение | y1 | y2 | x2 |
| 1 2 4 | –1 0 1 | 0 –1 1 | 0 0 1 |
Четвертое уравнение представляет собой тождество, параметры которого известны и необходимости в его идентификации нет.
Таким образом, все уравнения модели точно идентифицированы.
Пример 3.4. Произведем идентификацию следующей модели:
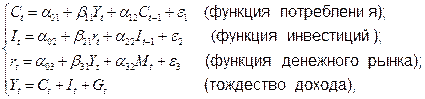
где C – расходы на потребление; Y – совокупный доход; I – инвестиции; r – процентная ставка; M – денежная масса; G – государственные расходы; t – текущий период; t – 1 – предыдущий период.
В данной модели число эндогенных переменных N = 4 (Ct, It, Yt, rt) и четыре экзогенных (Mt, Gt, Ct-1, It-1).
Для первого уравнения: G = 2(Ct, Yt – присутствуют), D = 3(Mt, Gt, It-1 – отсутствуют) и D > G – 1, поэтому уравнение сверхидентифицируемо (необходимое условие). Для проверки на достаточное условие идентификации выпишем матрицу коэффициентов при переменных, не входящих в первое уравнение:
| Уравнение | It | rt | It–1 | Mt | Gt |
| 2 3 4 | –1 0 1 | b21 –1 0 | a22 0 0 | 0 a32 0 | 0 0 1 |
Минор 3-го порядка данной матрицы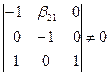 
, следовательно ранг матрицы равен 3 ³ N – 1, т.е. достаточное условие идентификации выполняется.
Для второго уравнения: G = 2(It, rt – присутствуют), D = 3(Mt, Gt, Ct-1 – отсутствуют) и D > G – 1, поэтому уравнение сверхидентифицируемо.
Выпишем матрицу коэффициентов при переменных, не входящих во второе уравнение:
| Уравнение | Ct | Yt | Ct–1 | Mt | Gt |
| 1 3 4 | –1 0 1 | b11 b31 –1 | a12 0 0 | 0 a32 0 | 0 0 1 |
Минор 3-го порядка данной матрицы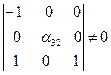 
, следовательно, ранг матрицы равен 3 ³ N – 1, т.е. достаточное условие идентификации выполняется.
Для третьего уравнения: G = 2(Yt, rt – присутствуют), D = 3(Gt, Ct-1, It-1 – отсутствуют) и D > G – 1, поэтому уравнение сверхидентифицируемо.
Выпишем матрицу коэффициентов при переменных, не входящих в третье уравнение:
| Уравнение | Ct | Ct–1 | It | It–1 | Gt |
| 1 2 4 | –1 0 1 | a12 0 0 | 0 –1 1 | 0 a22 0 | 0 0 1 |
Минор 3-го порядка данной матрицы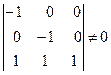 
, следовательно, ранг матрицы равен 3 ³ N – 1, т.е. достаточное условие идентификации выполняется.
Четвертое уравнение представляет собой тождество, параметры которого известны и необходимости в его идентификации нет.
Таким образом, все уравнения модели сверхидентифицированы.
Ненулевое ограничение
Добавление экзогенной переменной не есть единственный способ, который может привести к идентифицируемости уравнения. В некоторых случаях неидентифицируемая модель может быть идентифицируема путем задания соотношения между структурными коэффициентами.
Рассмотрим неидентифицируемую модель спроса и предложения (3.10).
Улучшим спецификацию модели, введя ограничения на коэффициенты s = –e:
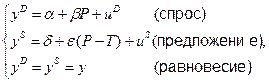(3.13)
Благодаря введению ограничения на коэффициенты уравнение предложения также стало идентифицируемым.
Действительно, при использовании ИП можно рассмотреть новую версию модели как систему из четырех уравнений:
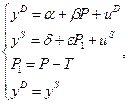(3.14)
где P1 – цена товара для продавца (сумма, остающаяся у него после уплаты налога).
Последние два уравнения системы (3.14) являются уравнениями-тождествами и не требуют проверки на идентификацию.
Переменная T не включена в уравнение спроса, поэтому она может использоваться как инструментальная для P. Точно так же эта переменная не включена в уравнение предложения, поэтому она может использоваться как инструментальная для P1.
В итоге модель в целом является точно идентифицируемой.
Вывод. Ненулевое ограничение позволяет исключить одну объясняющую переменную из уравнения. Если эта переменная эндогенная, для нее не нужно искать инструментальную переменную, если экзогенная, то она освобождается на роль инструментальной для одной из эндогенных переменных, оставшихся в уравнении.
Пример 3.5. Опишем процедуру оценивания структурной модели (3.13). Модель имеет две эндогенные переменные (Y , P) и одну экзогенную (T).
Было показано, что исходная модель точно идентифицируема, и поэтому для оценки ее структурных коэффициентов используем КМНК.
Разрешая исходную систему относительно Y , P, получим приведенную систему
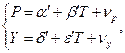
где
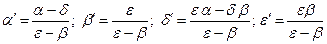(3.15)
Пусть имеются следующие наблюдений:
| T | 0 | 2 | 5 | 8 | 10 | 12 | 14 |
| P | 40 | 42 | 43 | 44 | 45 | 48 | 49 |
| Y | 70 | 68 | 63 | 61 | 60 | 56 | 52 |
Оцененные уравнения приведенной системы, полученные по выборочным данным с использованием МНК, есть:
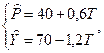
т.е. оценки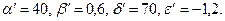 
Тогда соотношения (3.15) имеют вид:
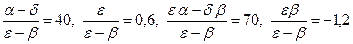
Отсюда получаем следующие оценки структурных коэффициентов:
a = 150, b = –2, d = –50, e = 3.
Замечание. Перейти от приведенной формы модели к структурной с учетом соотношения (3.14) можно сделать также следующим образом.
Выразив T из первого уравнения приведенной формы в виде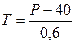 
и подставив его во второе, получим 
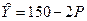, т.е. a = 150, b = –2.
Выразив T из первого уравнения приведенной формы в виде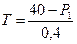 
, где P1= P – T и подставив его во второе, получим 
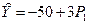, т.е. d =–50, e = 3.
Анализ методов оценивания
Приступать к оцениванию того или иного структурного уравнения системы имеет смысл после того, как установлено его идентифицируемость. Для установления идентифицируемости можно использовать ИП.
Для решения точно идентифицируемого уравнения применяется КМНК, а для решения сверхидентифицированного уравнения – ДМНК.
Анализ рассмотренных примеров позволяет сформулировать их основные этапы.
Этапы КМНК:
1. Структурная модель преобразуется в приведенную форму.
2. Для каждого приведенного уравнения обычным МНК оцениваются приведенные коэффициенты.
3. Оценки приведенных коэффициентов преобразуются в оценки параметров структурных уравнений.
Этапы ДМНК:
1. На основе приведенной формы модели получают для сверхидентифицированного уравнения теоретические (расчетные) значения эндогенных переменных, содержащихся в правой части уравнения.
2. Подставляя теоретические значения эндогенных переменных вместо их фактических значений в сверхидентифицируемое уравнение и применяя обычный МНК, определяют его структурные коэффициенты.
Метод получил название двухшагового, так как МНК используется дважды: при нахождении теоретических значений эндогенных переменных из приведенной формы модели и при определении структурных коэффициентов по теоретическим значениям эндогенных переменных и исходным данным экзогенных переменных.
Сверхидентифицируемая структурная модель может быть двух типов:
– все уравнения системы сверхидентифицируемы;
– система наряду со сверхидентифицируемыми содержит точно идентифицируемые уравнения.
Если все уравнения системы сверидентифицируемы, то для оценки структурных коэффициентов каждого уравнения используется ДМНК. Если в системе есть точно идентифицируемые уравнения, то структурные коэффициенты по ним находятся из системы приведенных уравнений.
Для точно идентифицируемых уравнений ДМНК дает тот же результат, что и КМНК.
Пример 3.6. Рассмотрим следующую идентифицируемую эконометрическую модель с двумя эндогенными (y1, y2) и двумя экзогенными (x1, x2) переменными:
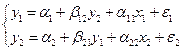(3.16)
Имеются следующие выборочные данные (у. е.):
| y1 | y2 | x1 | x2 |
| 2 | 5 | 1 | 3 |
| 3 | 6 | 2 | 1 |
| 4 | 7 | 3 | 2 |
| 5 | 8 | 2 | 5 |
| 6 | 5 | 4 | 6 |
Для точно идентифицируемой структурной модели применим КМНК.
Приведенная форма модели есть:
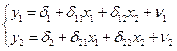
Оцененные уравнения приведенной системы, полученные по выборочным данным с использованием МНК, есть
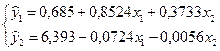(3.17)
Перейдем от приведенной формы модели к структурной.
Для этой цели из первого уравнения приведенной формы модели надо исключить x2, выразив его из второго уравнения приведенной формы:
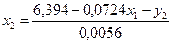
и подставить в первое, а из второго уравнения приведенной формы модели следует исключить x1, выразив его из первого уравнения приведенной формы:
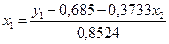
и подставить во второе.
В результате получим следующую структурную форму модели:
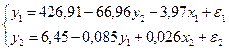(3.18)
Замечание. Покажем, что для точно идентифицируемых уравнений ДМНК дает тот же результат, что и КМНК
Из уравнений (3.17) можно найти расчетные значения эндогенных переменных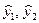 
. Подставляя их вместо фактических y1, y2 в правую часть структурной модели (3.16) и применяя обычный МНК к каждому уравнению модели, получим тот же результат, что и КМНК.
Расчетные данные для использования ДМНК приведены в таблице:
| y1 |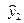 
| x1 | y2 | 
| x2 | |
| 2 | 6,303 | 1 | 5 | 2,657 | 3 | |
| 3 | 6,242 | 2 | 6 | 2,763 | 1 | |
| 4 | 6,164 | 3 | 7 | 3,989 | 2 | |
| 5 | 6,220 | 2 | 8 | 4,256 | 5 | |
| 6 | 6,070 | 4 | 5 | 6,334 | 6 |
Пример 3.7. В идентифицируемой модели (3.16) примера 3.6 наложим ограничение на ее параметры b12 = a11, тогда придем к модели:
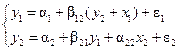(3.19)
В результате первое уравнение стало сверхидентифицируемым:
G = 1(y1), D = 1(x2) и D > G – 1.
Второе уравнение не изменилось и является точно идентифицируемым:
G = 2(y1, y2), D = 1(x1) и D = G – 1.
При использовании тех же данных, что и в примере 3.6, получим ту же систему приведенных уравнений:
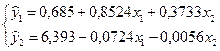(3.20)
Для определения структурных коэффициентов второго, точно идентифицируемого уравнения системы (3.19) применяем КМНК. Его структурная форма, найденная из системы приведенных уравнений та же, что и в примере 3.6.
Для определения структурных коэффициентов первого, сверхидентифицируемого уравнения системы (3.19) используем ДМНК. На основе второго уравнения приведенной системы (3.20) находим расчетные значения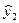 
эндогенной переменной. Подставляя их вместо фактических y2 в первое уравнение системы (3.19) и применяя обычный МНК, получим решение поставленной задачи.
Исходные данные при использовании ДМНК следующие:
| y1 | x1 |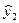
| 
|
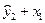
| 2 | 1 | 6,304 | 7,304 |
| 3 | 2 | 6,242 | 8,242 |
| 4 | 3 | 6,164 | 9,164 |
| 5 | 2 | 6,220 | 8,220 |
| 6 | 4 | 6,069 | 10,069 |
Окончательно, рассматриваемая система уравнений составит:
.
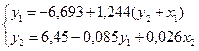Дата: 2019-02-02, просмотров: 229.
