В структурном уравнении функции потребления в качестве инструментальных переменных для Yt можно использовать как It, так и Gt. Полученные при этом оценки (a, b) будут различаться, но в обоих случаях они состоятельны.
Наилучшее решение в данном случае – применение инструментальной переменной, которая является комбинацией It и Gt.
Структурное уравнение с избыточным числом экзогенных переменных, которые можно использовать как инструментальные, является переопределенным (сверхидентифицируемым).
Двухшаговый метод наименьших квадратов
Двухшаговый МНК можно рассматривать как частный случай инструментальных переменных. В методе ИП было показано, что структурное уравнение функции потребления оказалось переопределенным и сразу две переменные It и Gt можно использовать для Yt.
Однако вместо их раздельного применения можно предложить их комбинацию 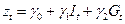 . В этом случае требуется оценить значения коэффициентов
. В этом случае требуется оценить значения коэффициентов 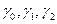 .
.
Фактически вместо zt можно использовать оценку 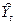 приведенного уравнения Yt, т.е.
приведенного уравнения Yt, т.е. 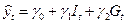 .
.
Подставляя расчетные значения 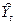 вместо фактических значений в структурное уравнение функции потребления, получим уравнение
вместо фактических значений в структурное уравнение функции потребления, получим уравнение
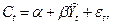
которое оценивается обычным МНК. При этом оценки структурных коэффициентов будут состоятельными.
Двухшаговый МНК можно рассматривать как способ конструирования наилучшей из возможных комбинаций инструментальных переменных, если в уравнении имеется избыток экзогенных переменных, которые можно использовать как инструментальные.
Пример 3.2. Для некоторой страны имеются данные (у. е.) о совокупном доходе Y, объеме потребления C, инвестициях I и государственных расходах G, полученные за 10 лет:
| Ct | 195 | 203 | 210 | 200 | 215 | 215 | 210 | 215 | 225 | 220 |
| It | 10 | 20 | 30 | 20 | 10 | 20 | 30 | 20 | 15 | 30 |
| Gt | 20 | 10 | 20 | 40 | 30 | 10 | 20 | 10 | 40 | 20 |
| Yt | 225 | 233 | 260 | 260 | 255 | 245 | 260 | 245 | 280 | 270 |
Построим функцию потребления, используя модель Кейнса формирования доходов (3.8).
Непосредственное оценивание структурного уравнения функции потребления обычным МНК приводит к следующим результатам:
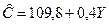 ,
,
т.е. оценки 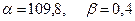 .
.
Было показано, что исходная модель (3.8) сверхидентифицируема, поэтому для оценки ее структурных коэффициентов используем ДМНК.
Расчетные значения эндогенной переменной Y, полученные МНК,
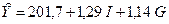 .
.
Подставим расчетные значения 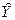 вместо фактических значений в структурное уравнение (3.8) функции потребления и оценим полученное уравнение обычным МНК:
вместо фактических значений в структурное уравнение (3.8) функции потребления и оценим полученное уравнение обычным МНК:
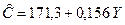 ,
,
т.е. оценки 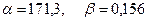 .
.
Оценки структурных коэффициентов функции потребления, полученные ДМНК, являются состоятельными.
Неидентифицируемость
Рассмотрим следующую модель спроса и предложения:
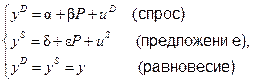
где P – цена товара, а uD, uS – случайные члены.
Переменные Y, P являются эндогенными, и их значения определяются в процессе установления равновесия.
В рассматриваемой модели нет экзогенных переменных, поэтому ни одно из этих уравнений не является идентифицируемым. Чтобы модель имела статистическое решение, в нее вводятся экзогенные переменные.
Предположим, что продавцы товара облагаются специальным налогом T, который они должны платить с выручки. При этом уравнение спроса останется неизменным, если переменная P означает рыночную цену, а уравнение предложения изменится:
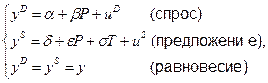 (3.10)
(3.10)
где T – экзогенная переменная.
Уравнение спроса будет идентифицируемым, поскольку переменная T не включена в него и может выступать как инструментальная для P, а уравнение предложения – неидентифицируемым.
Включим в уравнение спроса экзогенную переменную x – доход на душу населения:
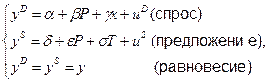 (3.11)
(3.11)
Экзогенную переменную x можно использовать как инструментальную вместо P для уравнения предложения.
В итоге получили в целом точно идентифицируемую модель спроса и предложения.
Пусть структурное уравнение спроса имеет временной тренд (скажем, потому что привычки медленно меняются со временем):
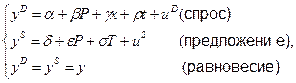 (3.12)
(3.12)
где t – переменная времени, а r – коэффициент при ней.
В модели спроса имеются две экзогенные переменные x, t, которые можно использовать в качестве инструментальных для P в уравнении предложения.
В итоге получили сверхидентифицируемое уравнение предложения, и точно идентифицируемое уравнение спроса.
Дата: 2019-02-02, просмотров: 318.