Зубчатые передачи классифицируют по геометрическим и функциональным особенностям: по взаимному расположению зубчатых колес- с внешним зацеплением и внутренним зацеплением; по характеру движения осей - простые, имеющие неподвижные геометрические оси и планетарные, у которых оси одного или нескольких колес подвижны; по направлению зубьев- прямые и криволинейные; по профилю зуба - эвольвентные, циклоидные и профили Новикова, в которых взаимодействуют выпуклый профиль зуба одного колеса и вогнутый профиль зуба другого; по конструктивному исполнению - открытые ( без корпуса) и закрытые в пыленепроницаемом корпусе, являющийся одновременно картером для масла; по передаваемой мощности: силовые и кинематические; по частоте вращения ведомого вала- понижающие (редукторы) и повышающие (мультипликаторы).
Цилиндрическая зубчатая передача. Эвольвентное зацепление. Основной закон зацепления. Линия зацепления. Угол зацепления.
Боковая поверхность зуба очерчена по эвольвенте. Эвольвента – это развёртка окружности (основной окружности в ЗП).
Для этого необходимо чтобы зубья зубчатых колёс были очерчены по кривой, у которой общая нормаль, проведённая через точку касания профилей зубьев, всегда проходит через одну и ту же точку на линии зацепления, называемую полюсом зацепления[
Геометрическое место точек контакта профилей, которое они занимают в процессе работы пары зубьев, называется линией зацепления.
Угол α, образованный перпендикуляром к межосевой линии с линией зацепления называется углом зацепления.
Основные параметры прямозубого цилиндрического зубчатого колеса эвольвентного профиля.
Модуль – линейная величина в π раз меньшая шага зубьев Р по делительной окружности.
Модуль стандартизован.
Окружность со стандартным модулем называется делительной окружностью. Она делит зуб на две части: головку и ножку.
Высота головки зуба. Головка – часть зуба, заключённая между делительной окружностью и окружностью вершин.
Высота ножки зуба. Ножка – часть зуба, заключённая между делительной окружностью и окружностью впадин.
Синтез зубчатых механизмов.
Синтез зубчатых механизмов – это процесс поиска начальных (сопряженных) профилей зубьев, формирующих геометрические параметры звеньев зубчатого механизма с целью обеспечения заданных условий.
Синтез зубчатых механизмов выполняется в два этапа: структурный синтез и метрический синтез.
На этапе структурного синтеза осуществляется формирование структурной схемы механизма, т. е. обосновываются число подвижных звеньев и видов движений, ими совершаемых; количество элементов стойки; число, класс и подвижность кинематических пар; количество и вид кинематических цепей, а также дополнительно обосновывается введение в структуру механизма каждой избыточной связи и местной подвижности.
Этап метрического синтеза предусматривает определение геометрических параметров зубчатых колес, формирующих качественные показатели зубчатого механизма, а также обеспечивающих выполнение основных условий работоспособности механизмов данного вида.
18. Планетарные механизмы и их отличительные особенности. Передаточное число и синтез планетарных механизмов. Пример.
Каждый планетарный механизм состоит из
Центральных (солнечных и корончатых) колес с неподвижными геометрическими осями
Колес, называемых сателлитами, оси которых перемещаются в пространстве с помощью рычага « H», называемого водилом
Планетарные передачи по сравнению с обычными
Имеют меньшие габариты
Могут иметь две и более степеней подвижности
Имеют более низкий КПД из-за относительных перемещений звеньев, вызванных подвижностью осей
Требуют более высокой точности изготовления
Планетарные механизмы – сложные ЗП в составе которых имеются сателлиты, т.е. колёса с подвижными осями вращения
Синтез планетарного механизма заключается в подборе чисел зубьев Z1,Z2,Z3 и определении числа сателлитов k.
Обычно принимают k=3 ( в 99%).
Подбор чисел зубьев должен осуществляться с учетом как общих условий синтеза зубчатых механизмов, так и условий, учитывающих специфику структуры механизмов данного вида, т. е. на данном этапе синтеза необходимо обеспечить:
1)заданное передаточное число с требуемой точностью;
2)соосность входного и выходного звеньев;
3)соседство сателлитов;
4)сборку механизма;
5)отсутствие подреза зубьев колес с внешними зубьями;
6)отсутствие заклинивания зубьев колес во внутреннем зацеплении;
7)обеспечение минимальных габаритных размеров механизма.
19. Метод Виллиса для определения передаточных чисел планетарных механизмов. Пример.
При исследовании сателлитных (планетарных) механизмов используют метод обращения движения (метод Виллиса).Относительное движение звеньев не изменится, если этим звеньям механизма сообщить дополнительное вращение с какой-либо угловой скоростью.
Сообщим звеньям механизма 1, 2, Н дополнительное вращение с угловой скоростью –ωН.
Тогда угловая скорость водила станет равной нулю; для остальных звеньев получим:
Для звена 1: 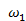 -
- 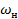 =
= 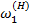
для звена 2: 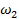 -
- 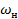 =
= 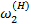
Дата: 2019-02-02, просмотров: 440.