Основные понятия теории механизмов и машин: машина, механизм, звено механизма, кинематическая пара.
Машина – устройство, выполняющее механические движения, для преобразования энергии, материалов и информации с целью замены или облегчения физического и умственного труда человека.
1. Энергетические машины, в которых какой либо вид энергии преобразуется в механическую энергию или наоборот. К этой группе относятся как машины-двигатели (двигатели внутреннего сгорания транспортных средств, электродвигатели и т. п.) так и машины - преобразователи (компрессоры, электрические генераторы и т. п.).
2. Технологические или рабочие машины, предназначенные для выполнения производственных процессов по изменению формы, свойств и положения объектов труда (металлорежущие станки, литьевые машины, автомобили и т.п.).
3. Информационные машины, в которых происходит преобразование вводимой информации для контроля, регулирования и управления технологическими процессами (вычислительные и др. машины).
Механизм - часть машины, в котором рабочий процесс реализуется путем выполнения определенных механических движений. Механизмом называют совокупную систему взаимосвязанных тел, предназначенных для преобразования движения одного или нескольких тел в требуемые движения других тел.
Твердое тело, входящее в состав механизма, называют звеном. Звенья, обладающие относительной подвижностью, называются подвижными. Неподвижное звено механизма называют стойкой или направляющей и обозначают одной цифрой. Звено, которому сообщается движение, преобразуемое в требуемое движение других тел, называют входным звеном. Звено, совершающее движение, для выполнения которого предназначен механизм, называют выходным звеном. Остальные подвижные звенья называются промежуточными.
Соединение двух соприкасающихся звеньев, допускающих их относительное движение, называется кинематической парой.
Кинематические пары могут быть плоскими или пространственными. В первом случае относительное движение сочлененных звеньев возможно лишь в параллельных плоскостях во втором случае – и в непараллельных плоскостях.
Структурный анализ механизмов.
Структурный анализ механизма – это определение числа степеней свободы механизма и разбивка механизма на структурные группы Асура и группу начальных звеньев, проводимая в порядке, обратном структурному синтезу. Число W степеней свободы звеньев пространственной кинематической цепи относительно стойки определяется формулой
W = 6n – 5p5 – 4p4 – 3p3 – 2p2 – p1
где n – число подвижных звеньев, p5 , p4 , p3 и т. д. – число кинематических пар пятого, четвертого, третьего и т. д. класса. Эта структурная формула пространственной кинематической цепи предложена А. П. Малышевым в 1923 году. Структурная формула плоской кинематической цепи, определяющая число степеней свободы относительно стойки, принимает вид. W = 3n – 2p5 –p4 Такая формула с учетом лишь пар пятого класса была предложена П. Л. Чебышевым в 1869 году. Группа Ассура - кинематическая цепь, которая имеет в механизме число степеней свободы W =0 и не распадается на более простые кинематические цепи с таким же W . Диада это структурная группа, состоящая из двух звеньев с тремя кинематическими парами. Начальные звенья – это те, которым приписывают обобщенные координаты, их направления движений обозначают на кинематических схемах механизма стрелками. Обобщенные координаты механизма – независимые между собой координаты, определяющие положение всех звеньев относительно стойки.
План положений механизма. Определение крайних положений механизма и хода рабочего органа.
План положений механизма – это масштабное графическое изображение кинематической схемы механизма для заданного положения ведущего звена.
План положений механизма вычерчивается в определенном масштабе
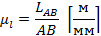
где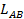 
- фактическая длина шатуна, м
АВ - длина отрезка, изображающего шатун на чертеже, мм
Кинематическое исследование механизма. Определение скоростей точек и звеньев механизма. Пример.
Кинематический анализ (исследование) механизмов – это аналитический и графический процесс расчета, в результате которого определяются
перемещения и траектории;
скорости;
ускорения.
Методы кинематического анализа:
а) графический или графоаналитический – нагляден, но менее точен;
б) аналитический – точный, но более сложный.
Определение скоростей точек механизма для заданного положения ведущего звена произведем графоаналитическим методом
Кинематическое исследование механизма. Определение ускорений точек и звеньев механизма. Пример
Кинематический анализ (исследование) механизмов – это аналитический и графический процесс расчета, в результате которого определяются
перемещения и траектории;
скорости;
ускорения.
Методы кинематического анализа:
а) графический или графоаналитический – нагляден, но менее точен;
б) аналитический – точный, но более сложный.
Определение ускорений точек механизма Так как кривошип вращается с постоянной угловой скоростью,
ускорение точки В кривошипа равно нормальному
Силовое исследование группы начальных звеньев. Уравновешивающий момент, реакция стойки на кривошип. Пример.
Синтез зубчатых механизмов.
Синтез зубчатых механизмов – это процесс поиска начальных (сопряженных) профилей зубьев, формирующих геометрические параметры звеньев зубчатого механизма с целью обеспечения заданных условий.
Синтез зубчатых механизмов выполняется в два этапа: структурный синтез и метрический синтез.
На этапе структурного синтеза осуществляется формирование структурной схемы механизма, т. е. обосновываются число подвижных звеньев и видов движений, ими совершаемых; количество элементов стойки; число, класс и подвижность кинематических пар; количество и вид кинематических цепей, а также дополнительно обосновывается введение в структуру механизма каждой избыточной связи и местной подвижности.
Этап метрического синтеза предусматривает определение геометрических параметров зубчатых колес, формирующих качественные показатели зубчатого механизма, а также обеспечивающих выполнение основных условий работоспособности механизмов данного вида.
18. Планетарные механизмы и их отличительные особенности. Передаточное число и синтез планетарных механизмов. Пример.
Каждый планетарный механизм состоит из
Центральных (солнечных и корончатых) колес с неподвижными геометрическими осями
Колес, называемых сателлитами, оси которых перемещаются в пространстве с помощью рычага « H», называемого водилом
Планетарные передачи по сравнению с обычными
Имеют меньшие габариты
Могут иметь две и более степеней подвижности
Имеют более низкий КПД из-за относительных перемещений звеньев, вызванных подвижностью осей
Требуют более высокой точности изготовления
Планетарные механизмы – сложные ЗП в составе которых имеются сателлиты, т.е. колёса с подвижными осями вращения
Синтез планетарного механизма заключается в подборе чисел зубьев Z1,Z2,Z3 и определении числа сателлитов k.
Обычно принимают k=3 ( в 99%).
Подбор чисел зубьев должен осуществляться с учетом как общих условий синтеза зубчатых механизмов, так и условий, учитывающих специфику структуры механизмов данного вида, т. е. на данном этапе синтеза необходимо обеспечить:
1)заданное передаточное число с требуемой точностью;
2)соосность входного и выходного звеньев;
3)соседство сателлитов;
4)сборку механизма;
5)отсутствие подреза зубьев колес с внешними зубьями;
6)отсутствие заклинивания зубьев колес во внутреннем зацеплении;
7)обеспечение минимальных габаритных размеров механизма.
19. Метод Виллиса для определения передаточных чисел планетарных механизмов. Пример.
При исследовании сателлитных (планетарных) механизмов используют метод обращения движения (метод Виллиса).Относительное движение звеньев не изменится, если этим звеньям механизма сообщить дополнительное вращение с какой-либо угловой скоростью.
Сообщим звеньям механизма 1, 2, Н дополнительное вращение с угловой скоростью –ωН.
Тогда угловая скорость водила станет равной нулю; для остальных звеньев получим:
Для звена 1: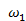 
- 
= 
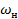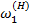
для звена 2: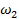 
- = 
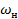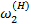
Расчет на прочность при сдвиге. Закон Гука. Примеры расчета на срез.
Гук экспериментально установил зависимость между касательным напряжением t и углом сдвига g (до тех пор пока не произошел срез):
t=G*g закон Гука при сдвиге: касательные напряжения t при сдвиге прямо пропорциональны углу сдвига g .
G - модуль упругости при сдвиге (модуль упругости второго рода) характеризует жесткость материала
Расчет:
Закон парности касательных напряжений: касательные напряжения t при сдвиге всегда направлены навстречу друг другу
Пример: Расчет болтового соединения на срез.
Дано: F – поперечная сила;
Материал болта сталь (допускаемое касательное напряжение = 60 МПа)
Найти: минимальный диаметр болта из условия прочности на срез
К концам стальных листов приложены силы F.
Касательные напряжения, возникающие в плоскости среза (на стыке листов) определяются по условию прочности при сдвиге
Основные понятия теории механизмов и машин: машина, механизм, звено механизма, кинематическая пара.
Машина – устройство, выполняющее механические движения, для преобразования энергии, материалов и информации с целью замены или облегчения физического и умственного труда человека.
1. Энергетические машины, в которых какой либо вид энергии преобразуется в механическую энергию или наоборот. К этой группе относятся как машины-двигатели (двигатели внутреннего сгорания транспортных средств, электродвигатели и т. п.) так и машины - преобразователи (компрессоры, электрические генераторы и т. п.).
2. Технологические или рабочие машины, предназначенные для выполнения производственных процессов по изменению формы, свойств и положения объектов труда (металлорежущие станки, литьевые машины, автомобили и т.п.).
3. Информационные машины, в которых происходит преобразование вводимой информации для контроля, регулирования и управления технологическими процессами (вычислительные и др. машины).
Механизм - часть машины, в котором рабочий процесс реализуется путем выполнения определенных механических движений. Механизмом называют совокупную систему взаимосвязанных тел, предназначенных для преобразования движения одного или нескольких тел в требуемые движения других тел.
Твердое тело, входящее в состав механизма, называют звеном. Звенья, обладающие относительной подвижностью, называются подвижными. Неподвижное звено механизма называют стойкой или направляющей и обозначают одной цифрой. Звено, которому сообщается движение, преобразуемое в требуемое движение других тел, называют входным звеном. Звено, совершающее движение, для выполнения которого предназначен механизм, называют выходным звеном. Остальные подвижные звенья называются промежуточными.
Соединение двух соприкасающихся звеньев, допускающих их относительное движение, называется кинематической парой.
Кинематические пары могут быть плоскими или пространственными. В первом случае относительное движение сочлененных звеньев возможно лишь в параллельных плоскостях во втором случае – и в непараллельных плоскостях.
Классификация кинематических пар (КП). Классы КП. Высшие и низшие КП.
Соединение двух соприкасающихся звеньев, допускающих их относительное движение, называется кинематической парой.
Кинематические пары могут быть плоскими или пространственными. В первом случае относительное движение сочлененных звеньев возможно лишь в параллельных плоскостях во втором случае – и в непараллельных плоскостях. Кинематические пары можно классифицировать по числу связей, налагаемых на относительное движение соприкасающихся звеньев или по числу степеней свободы. Известно, что свободное твердое тела в пространстве имеет шесть степеней свободы: три поступательных движения вдоль осей декартовой системы координат и три вращательных движения вокруг этих осей. Если звено вступает в кинематическую пару с другим звеном, то контакт между ними накладывает на их взаимное движение связи. Если таких связей будет наложено шесть, то кинематическая пара перестает существовать, т. к. образуется неподвижное соединение этих звеньев, то есть образуется новое звено. Если же число таких связей, наложенных элементами пары на взаимное движение её звеньев, будет U < 6, то число степеней свободы W такой пары определится формулой W = 6 – U. Очевидно, что 0 < U < 6. Следовательно, число связей кинематической пары может быть в пределах от одного до пяти. В связи с этим все кинематические пары по числу связей могут делиться на пять классов. К первому классу будем относить кинематические пары, налагающие на относительное движение звеньев одну связь, ко второму классу – пары, имеющие две связи и так далее. В этом случае пара пятого класса будет иметь пять связей и только одну степень свободы относительного движения звеньев. Связанная система звеньев, образующих между собой кинематические пары, называется кинематической цепью (рис. 34). Кинематические цепи подразделяются на открытые и замкнутые, плоские и пространственные. Открытой кинематической цепью называют такую, в которой имеются звенья, входящие только в одну кинематическую пару (рис. 34 а, в). Замкнутой кинематической цепью называют такую, в которой все звенья входят не менее чем в две кинематические пары (рис. 34 б, г). Плоские кинематические цепи образуются плоскими парами, в них точки
звеньев описывают траектории, лежащие в параллельных плоскостях. Кинематическая цепь называется пространственной, если точки её звеньев описывают неплоские траектории или траектории, лежащие в пересекающихся плоскостях. Наибольшее распространение на практике имеют плоские кинематические цепи. По виду звеньев, входящих в кинематическую цепь, последние разделяются на простые и сложные. Простой кинематической цепью называется такая цепь, в которой каждое звено входит не более чем в две кинематические пары (рис. 34 а, б). Сложной кинематической цепью называется такая, в которой имеется хотя бы одно звено, входящее более чем в две кинематические пары (рис. 34 в, г).
Дата: 2019-02-02, просмотров: 514.
