Приведение моментов сопротивления от одной оси вращения к другой может быть произведено на основании энергетического баланса системы. При этом потери мощности в промежуточных передачах учитываются введением в расчёты соответствующего КПД - 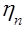. Обозначим через  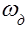угловую скорость вала двигателя, а  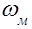- угловую скорость вала производственного механизма. На основании равенства мощностей получим:

 ,

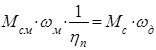отсюда

 ,

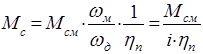где М_см - момент сопротивления производственного механизма, ;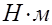

М_с – тот же момент сопротивления, приведённый к скорости вала двигателя, ;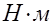

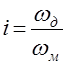 - передаточное число.

При наличии нескольких передач между двигателем и механизмом   ( см. рис.2.1 ) с передаточными числами i₁, i₂,…, i_n и соответствующими КПД 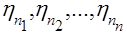 вала двигателя, определяется формулой:

.

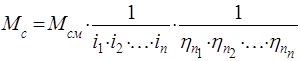Приведение сил сопротивления производится аналогично приведению моментов. Если скорость поступательного движения 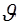, м/с, а угловая скорость вала двигателя 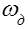, рад/с, то

,

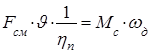гдеF_см – сила сопротивления производственного механизма, Н.

Отсюда приведённый к скорости вала двигателя момент сопротивления равен

.

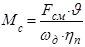В случае приведения вращательного движения к поступательному, приведённое усилие:

.

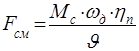Приведение моментов инерции к одной оси вращения основано на том, что суммарный запас кинетической энергии движущихся частей привода, отнесённый к одной оси, остаётся неизменным. При наличии вращающихся частей, обладающих моментом инерции I_д, I₁, I₂, …, I_n и угловыми скоростями 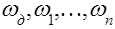 ( см. рис.2.1, а ), можно заменить их динамическое действие действием одного момента инерции, приведённого например, к скорости вала двигателя. В таком случае можно написать:

,

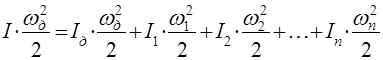отсюда результирующий или суммарный момент инерции, приведённый к валу двигателя:

,

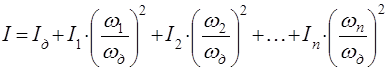где

I_д – момент инерции ротора двигателя и других элементов ( муфты, шестерни и т.п. ), установленных на валу двигателя.

Это соотношение следует из формулы, определяющей момент инерции тела массой m , кг,

,

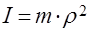где

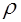 - радиус инерции, м.

Если сила тяжести выражена в ньютонах, то масса тела определяется из равенства:

,

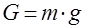где

g = 9,81 м/с² – ускорение свободного падения.

Момент инерции сплошного цилиндра относительно продольной оси вычисляется по формуле:

,

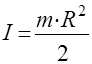где

R – радиус цилиндра, м.

Момент инерции сплошного цилиндрического тела, вращающегося вокруг своей оси:

,

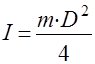где

m – масса тела, кг;

D – диаметр инерции тела, м.

Приведение масс, движущихся поступательно, осуществляется также на основании равенства запаса кинетической энергии:

.

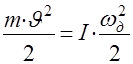Отсюда момент инерции, приведённый к валу двигателя:

.

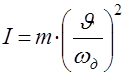Если механизм имеет вращающиеся и поступательно движущиеся элементы, то суммарный приведённый к валу двигателя момент инерции:

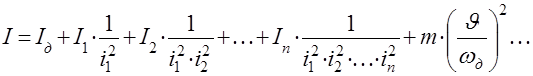
Для приведения момента инерции к поступательному движению нужно момент инерции заменить приведённой массой, т.е.

.

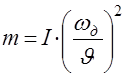Билет №3

1. Схема управления работой двух АД, исключающая их одновременную работу с тепловой защитой