Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОУ ВПО ЧЕРЕПОВЕЦКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

 

 

Факультет общих математических и естественнонаучных дисциплин

Кафедра химии

 

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

ПО  ДИСЦИПЛИНЕ

«ОБЩАЯ И НЕОРГАНИЧЕСКАЯ ХИМИЯ»

 

(Для студентов заочной формы обучения)

Часть 3

Учебно-методическое пособие

 

 

                                                       Специальности:    240301   Химическая технология

                                                        неорганических веществ;   280201 Охрана окру-

                                                           жающей  среды  и  рациональное  использование

                                                           природных ресурсов; 240801 Машины и аппара-

                             ты химических производств

 

 

Череповец

2007

 

 

Примеры решения задач по дисциплине «Общая и неорганическая химия» для студентов заочной формы обучения: В 3 ч. Ч. 3: Учеб.-метод. пособие. – Череповец: ГОУ ВПО ЧГУ, 2007. – 35 с.

 

 

Рассмотрено на заседании кафедры химии, протокол №  9 от 14.05. 07.

Одобрено редакционно-издательской комиссией факультета общих математических и естественнонаучных дисциплин ГОУ ВПО ЧГУ, протокол №  8 от 15.05. 07.

 

Составители:   О.А. Калько – канд. техн. наук, доцент;              

                      Ю.С. Кузнецова;

Н.В. Кунина

                          

 

Рецензенты:  С. Н. Балицкий  – канд. хим. наук, доцент (ГОУ ВПО ЧГУ);

                 Л.Ю. Кудрявцева – канд. техн. наук, доцент (ГОУ ВПО ЧГУ)

                      

 

 

Научный редактор: Г.А. Котенко – канд. хим. наук, профессор

 

 

                                                      © Калько О.А., Кунина Н.В.,

                                                           Кузнецова Ю.С., 2007

                                                      ©ГОУ ВПО Череповецкий государст-­

                                                                  венный  университет, 2007

 

ВВЕДЕНИЕ

Данное учебно-методическое пособие содержит краткие теоретические сведения и примеры решения задач по теме «Растворы» курса «Общая и неорганическая химия». Пособие предназначено для студентов заочной формы обучения в качестве вспомогательного руководства для самостоятельной работы при выполнении домашних контрольных работ. Содержание учеб­но-методического пособия соответствует государственному стандарту дисциплины «Общая и неорганическая химия» для химических специальностей.

 

 

РАСТВОРИМОСТЬ. СПОСОБЫ ВЫРАЖЕНИЯ

СОСТАВА РАСТВОРОВ

Примеры решения задач

 

Пример 1. Растворимость KClO₃ при 20 °С равна 7,3 г/100 г воды, а при 100 °C – 56,2 г/100 г воды. Какая масса хлората калия выкристаллизуется из 50,0 г раствора данной соли насыщенного при 100 °C, если раствор охладить до 20 °C?

Р е ш е н и е

При охлаждении раствора масса воды, остается постоянной, а масса растворенного вещества, а значит, и масса раствора в целом, меняются. Из определения растворимости следует, что при 100 °C раствор содержит 100,0 г воды и 56,2 г KClO₃. Масса такого раствора составляет (100 + 56,2) = 156,2 г. По пропорции определяем массу воды в 50 г раствора

156, 2 г раствора — 100,0 г Н₂О;

50,0 г раствора — m₁ г Н₂О;

Откуда m₁ = 32,0 г Н₂О.

Тогда масса соли в 50,0 г горячего раствора равна: (50,0 – 32,0) = 18,0 г.

    По значению растворимости при 20 °C определяем, сколько соли будет растворено в 32 г воды

в 100 г Н₂О — 7,3 г KClO₃;

в 32,0 г Н₂О — х₁ г KClO₃;

Откуда m₂ = 2,3 г KClO₃.

Тогда масса KClO₃, выкристаллизовавшаяся после охлаждения раствора, равна (18,0 – 2,3) = 15,7 г.

 

Пример 2. Рассчитайте массовую долю и моляльную концентрацию глюкозы в растворе, полученном путем растворения 25 г глюкозы (С₆Н₁₂О₆) в 100 см³ воды.

Р е ш е н и е

Находим массу раствора, считая плотность воды равной 1 г/см³

.

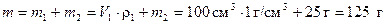Тогда по формуле (1) .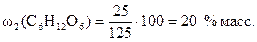

Для определения моляльной концентрации раствора найдем молярную массу глюкозы

М₂(С₆Н₁₂О₆) = 12·6 + 1·12 + 6·16 = 180 г/моль.

Тогда по формуле (3)  .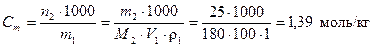

Пример 3. В дистиллированной воде объёмом 250 мл растворили кристаллогидрат FeSO₄ ·7H₂О массой 50 г. Определите массовую долю кристаллогидрата и безводного сульфата железа (II) в растворе.

Р е ш е н и е

Найдем массу раствора, считая плотность воды равной 1 г/мл

.

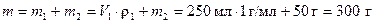Тогда по формуле (1) массовая доля кристаллогидрата FeSO₄ ·7H₂О

.

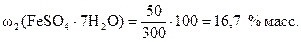Определяем молярную массу безводного сульфата железа (II) и молярную массу кристаллогидрата

М₂(FeSO₄) = 56 + 32 + 16·4= 152 г/моль;

М₂(FeSO₄ ·7H₂О) = 152 + 7·18 = 278 г/моль.

Массу безводной соли в 50 г FeSO₄ ·7H₂О определяем по пропорции

 1 моль (278 г) FeSO₄ ·7H₂О содержит 1 моль (152 г) FeSO₄ ;

50 г FeSO₄ ·7H₂О содержит       m₂ г FeSO₄ ;

Откуда           .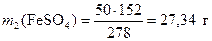

Массовая доля безводной соли FeSO₄ в 300 г раствора равна

 

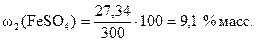
Пример 4. Вычислите массовую долю (% масс.), молярную и молярную эквивалентную концентрации растворенного вещества, а также определите моляльность и титр раствора, полученного при растворении 18 г фосфата калия в 250 см³ воды, если плотность раствора r = 1,31 г/см³ = = 1310 г/дм³.

Р е ш е н и е

Находим массу раствора, считая плотность воды равной 1 г/см³

.

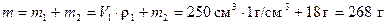Тогда по формуле (1)    .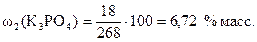

    Определяем молярную массу растворенного вещества

М₂(К₃РO₄) = 3∙39 + 31 + 4∙16 = 212 г/моль.

Молярную концентрацию находим по формуле (4)

 .

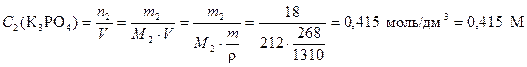    Для расчета молярной концентрации эквивалента вещества используем формулу (6)

,

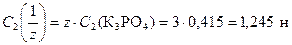где 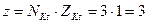; N_Kt – число катионов в 1 молекуле соли; Z_Kt – заряд катиона соли.

    Рассчитываем моляльную концентрацию раствора по формуле (3)

.

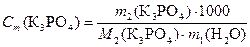
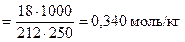    Вычисляем титр раствора по формуле (7)

 .

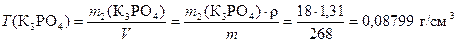Пример 5. Определите мольную долю сульфата алюминия в растворе с концентрацией 10 % масс.

Р е ш е н и е

Определяем молярные массы компонентов раствора

М₂(Al₂(SO₄)₃) = 2∙27 + 3∙(32 + 16·4) = 342 г/моль;

М₁(H₂О) = 18 г/моль.

По условию w₂(Al₂(SO₄)₃) = 10 % масс., значит в 100 г раствора содержится 10 г соли и 90 г воды. Тогда по формуле (8)

.

        

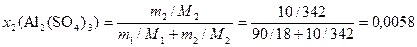Пример 6. Рассчитайте массовый процент Al₂(SO₄)₃ в растворе с мольной долей соли х₂ = 0,25.

Р е ш е н и е

Пусть общее количество раствора n = 1 моль, тогда мольная доля растворенного вещества будет равна числу моль данного компонента в растворе

.

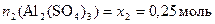Число моль растворителя определяем по формуле

.

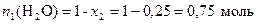Рассчитаем массы веществ, которые содержатся в 1 моль раствора

; .

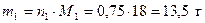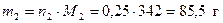Массовый процент Al₂(SO₄)₃ в растворе равен

 

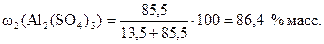
Пример 7. Рассчитайте, какой объём 2,5 %-ного раствора КMnO₄ и воды нужно взять для приготовления 40 мл 0,05 %-ного раствора. Плотность 0,05 %-ного раствора равна 1,003 г/мл, а 2,5 %-ного – 1,017 г/мл.

Р е ш е н и е

Примем обозначения для величин, указанных в условии задачи:

Исходный раствор: w₁  = 2,5 % масс.; r₁ = 1,0175 г/мл; V₁ – ?;

Конечный раствор: w₂  = 0,05 % масс.; r₂ = 1,003 г/мл; V₂ = 40 мл.

Приготовление раствора с концентрацией 0,05 % масс. из раствора с концентрацией 2,5 % масс. происходит путем разбавления последнего чистым растворителем, то есть водой, поэтому используем формулу (10). Из которой выражаем V₁

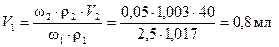
Объем воды найдем по формуле, считая плотность воды r(Н₂О) = 1 г/мл

.

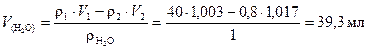       Пример 8. Сколько граммов 90 %-ного и 10 %-ного раствора серной кислоты необходимо взять для приготовления 800 г 40 %-ного раствора?

Р е ш е н и е

    Пользуясь правилом смешивания (иначе правилом креста), определяем соотношение весовых частей, в которых необходимо смешать 90 %-ный. и 10 %-ный растворы серной кислоты, чтобы получить 40 %-ный раствор по формуле (11)

m₁ / m₂ = (w₃ – w₂) / (w₁ – w₃) = (40 – 10) / (90 – 40) = 3/5.

    Таким образом, исходные растворы серной кислоты необходимо смешать в соотношении 3 : 5.

По условию задачи необходимо получить 800 г 40 %-ного раствора серной кислоты. Поэтому 800 г делим на две части пропорциональные полученному отношению

 ; .

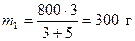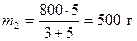    Следовательно, необходимо взять 300 г 90 %-ного и 500 г 10 %-ного раствора серной кислоты.

 

Пример 9. Какой объем 0,52 М раствора гидроксида натрия потребуется для нейтрализации 15,45 см³ раствора серной кислоты с массовой долей 3 %  масс. и плотностью 1,018 г/см³.

Р е ш е н и е

Объем гидроксида натрия следует находить по закону эквивалентов. Для этого необходимо пересчитать концентрацию раствора серной кислоты из % масс. в нормальность.

Находим массу раствора кислоты, используя объем и плотность

.

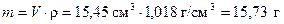Тогда из формулы (1) найдем массу серной кислоты

.

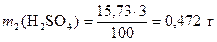    Определяем молярную массу эквивалента серной кислоты

М₂( 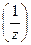Н₂SO₄) = .

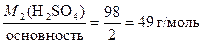По формуле (5) определяем нормальность раствора Н₂SO₄

 .

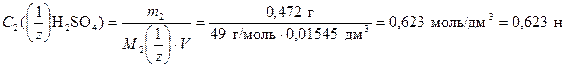По формуле (6) определяем нормальность раствора гидроксида натрия

.

Объем NaOH найдем по формуле (12)

 .

 

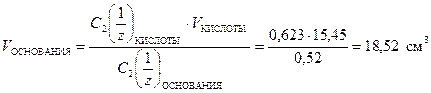Пример 10. Какое количество (см³) потребуется для приготовления 0,1 дм³ раствора серной кислоты с концентрацией 3,55 н из 96 %-ного Н₂SO₄ плотностью r = 1,836 г/см³.

Р е ш е н и е

    Массу Н₂SO₄, содержащуюся в растворе найдем из формулы (5)

 ;

 .

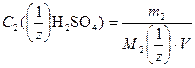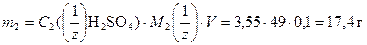    Объем 96 %-ного раствора серной кислоты, необходимый для приготовления 0,1 дм³ 3,55 н раствора найдем из формулы (1)

.

 

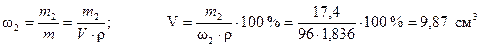Примеры решения задач

 

Пример 1. Вычислите давление насыщенного пара над раствором, содержащим 6,4 г нафталина (С₁₀Н₈) в 90 г бензола (С₆Н₆) при 20 °С. Давление насыщенного пара над чистым бензолом при данной температуре возьмите в справочнике.

Р е ш е н и е

Определим молярные массы нафталина (растворенное вещество) и бензола (растворитель)

М₂(С₁₀Н₈) = 128 г/моль;  М₁(С₆Н₆) = 78 г/моль.

По формуле (8) определяем мольную долю нафталина в растворе

.

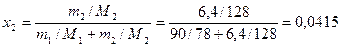Из справочника [8] при 20 °С для чистого бензола Р 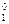 = 9953,82 Па. Тогда, из формулы (13) выразим давление насыщенного пара над раствором

.

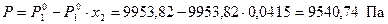Пример 2. Вычислите температуру кипения и температуру замерзания водного раствора фруктозы с массовой долей 5 % масс.

Р е ш е н и е

Поскольку массовая доля фруктозы равна 5 % масс., это значит, что в 100 г раствора содержится 5 г растворенного вещества и 95 г воды. Молярная масса фруктозы С₆Н₁₂О₆ равна М₂ = 180 г/моль. Тогда, по уравнению (3) моляльная концентрация раствора равна

.

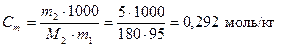Из справочника для растворителя выбираем

К_Э(Н₂О) = 0,52 (К·кг/моль); а К_К(Н₂О) = 1,86 (К·кг/моль).

По формуле (14) определяем изменение температуры кипения

DT_кип = К_Э × С _m  = 0,52 ×0,292 = 0,152 °С.

По формуле (15) определяем изменение температуры замерзания

DT_зам = К_К × С _m  = 1,86 ×0,292 = 0,543 °С.

Чистая вода кипит при 100°С и замерзает при 0 °С,а раствор глюкозы кипит при более высокой температуре, замерзает при более низкой

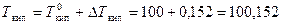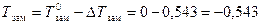 °С;

°С.

Пример 3. Рассчитайте осмотическое давление 20 %-ного водного раствора глюкозы (плотность раствора ρ = 1,08 г/мл = 1080 г/л) при 310 К, применяемого для внутривенного введения при отеке легкого. Каким будет этот раствор гипо-, гипер- или изотоническим по отношению к крови, если учесть, что Р_осм крови лежит в пределах  740 – 780 кПа?

Р е ш е н и е

Для определения осмотического давления необходимо перейти от процентной концентрации к молярной. Молярная масса глюкозы С₆Н₁₂О₆ равна М₂ = 180 г/моль. Тогда, по уравнению (4) молярная концентрация раствора равна

 . 

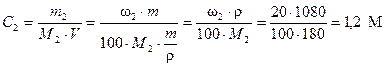По закону Вант-Гоффа (уравнение (18))

Р_осм = 1,2 × 8,314 × 310 = 3092,81 кПа.

Поскольку 3092,81 кПа > Р_осм(крови), то 20 %-ный раствор глюкозы является гипертоническим по отношению к крови.

 

Пример 4. Определить массу глюкозы С₆Н₁₂О₆ , которую должен содержать 1 дм³ раствора, чтобы быть изотоничным раствору, содержащему в 1 дм³ 9,2 г глицерина С₃Н₈О₃.

Р е ш е н и е

Определим молярную концентрацию глицерина по формуле (4)

С₂(С₃Н₈О₃) = 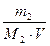= = 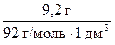0,1 моль/дм³.

При одинаковой температуре изотоничными будут растворы с одинаковой молярной концентрацией неэлектролита. Следовательно, масса глюкозы будет равна

m₂(С₆Н₁₂О₆) = С₂(С₃Н₈О₃) × M₂(С₆Н₁₂О₆) × V;

m₂(С₆Н₁₂О₆) = 0,1 моль/дм³ × 180 г/моль × 1 дм³ = 18 г.

    Пример 5. При растворении 0,4 г некоторого вещества в 10 г воды температура замерзания раствора понижается на 1,24°. Вычислить молекулярную массу растворенного вещества.

Р е ш е н и е

    По формуле (17)

M₂ = K_К × .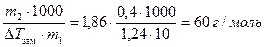

РАСТВОРЫ ЭЛЕКТРОЛИТОВ

Примеры решения задач

Пример 1. Раствор содержит 0,85 г хлорида цинка и 125 г воды, которая кристаллизуется при температуре –0,23 °С. Рассчитайте кажущуюся степень диссоциации хлорида цинка в данном растворе.

Р е ш е н и е

    Температура замерзания чистой воды равна Т 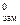 = 0 °С, тогда

DT_зам = Т 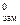 – T_зам = 0 – (–0,23) = 0,23 °С.

    Моляльность раствора рассчитаем по формуле (3)

.

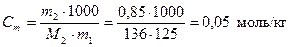Изотонический коэффициент для данного раствора определяем из формулы (36)

.

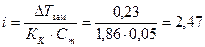Для соли CaCl₂ n = 3, тогда по уравнению (33) кажущаяся степень диссоциации равна

a = .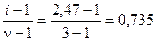

 

Пример 2.Определите концентрацию ионов ОН^– в 0,01 М растворе гидроксида аммония, если К_Д(NH₄OH) = 1,77 · 10^-5.

Р е ш е н и е

Данный электролит в водном растворе диссоциирует обратимо по схеме NH₄OH Û NH 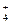 + ОН^–. Поскольку К_Д(NH₄OH) << 1, значит гидроксид аммония очень слабый электролит. Тогда для определения степени диссоциации NH₄ОН можно использовать формулу (25)

a =  .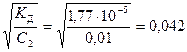

Концентрацию ионов ОН^– найдем по уравнению (20)

[ОН^–] = n× a ×C₂ = 1× 0,042× 0,01 = 4,2 · 10^-4.

Пример 3. Вычислите концентрацию ионов ОН ˉ в растворе, содержащем смесь NH₄OH (С₂ = 0,2 M) и NH₄Сl (С 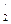 = 1 M), К_Д(NH₄OH) = = 1,77 · 10^-5.

Р е ш е н и е

Концентрация ионов ОН ˉ определяется уравнением диссоциации слабого электролита по схеме NH₄OH Û NH₄⁺ + OH ˉ .

Выражение для константы диссоциации имеет вид K_Д = .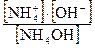

Тогда           [ОН ˉ] = .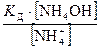

NH₄Сl  – сильный электролит, диссоциирует на ионы полностью по схеме NH₄Cl Û NH 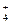 + Cl^–. Тогда [NH₄⁺] = С  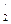= 1 моль/л, поскольку концентрацией ионов NH 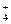, полученной за счет диссоциации слабого электролита NH₄OH, можно пренебречь. Отсюда

[ОН 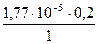^–] =  = 3,6×10^-6 моль/дм³.

 

Пример 4. Рассчитайте концентрации ионов в 0,01 М растворе K₂SO₄.

Р е ш е н и е

K₂SO₄ – сильный электролит, диссоциирует по уравнению K₂SO₄ ® 2K⁺ + SO 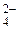. Следовательно, концентрации ионов определяем по формуле (21)

[K⁺] = 2× С₂ = 2 × 0,01 = 0,02 моль/дм³; [ SO 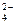] = С₂ = 0,01 моль/дм³.

 

Пример 5. Рассчитайте активность ионов водорода в 0,03 М растворе серной кислоты.

Р е ш е н и е

Н₂SO₄ − сильная двухосновная кислота, которая полностью распадается на ионы по уравнению Н₂SO₄ → 2H⁺ + SO 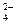. Тогда концентрации ионов из формулы (21) равны [Н⁺] = 2× 0,03 = 0,06 М; [SO 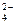] = 0,03 М. Ионную силу раствора рассчитаем по формуле (32)

I = ½ × (0,06·1² + 0,03 · 2²) = 0,09.

Коэффициент активности γ(Н⁺) найдем из справочника [8]. Для ионной силы I = 0,09   коэффициент активности однозарядного иона γ₊ = 0,847. Тогда по формуле (26)

а 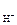 = [Н⁺] × g₊ = 0,06 ×0,847 = 0,051 М.

Пример 6. Определите активность нитрата стронция в растворе с концентрацией 0,06 моль/кг?

Р е ш е н и е

Sr(NO₃)₂ диссоциирует по уравнению Sr(NO₃)₂ Û Sr²⁺ + 2 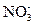. Так как С _m = 0,06 моль/кг, то равновесные концентрации ионов равны 

[Sr²⁺] = 0,06 моль/кг; [ 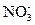] = 2 × 0,06 = 0,12 моль/кг.

По уравнению (32) находим ионную силу раствора

I = 1/2 × ([Sr²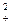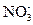⁺] × z  + [ ] × z ) = 1/2×(0,06×2² + 0,12×1²) = 0,18.

По формуле (31) вычисляем средний ионный коэффициент активности электролита

lg g_± = – 0,5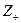×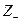½ × ½× 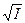 = – 0,5×½2 × 1½×  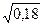= –0,424.

Следовательно, f_± = 10^–0,424 = 0,376.

Среднюю ионную моляльность электролита найдем по формуле (30)

С_± = .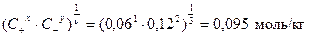

Активность Sr(NO₃)₂ оцениваем по уравнению (27)

а₂ = 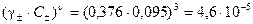 моль/кг.

 

 

Примеры решения задач

 

Пример 1. Вычислите степень диссоциации, концентрацию ионов водорода и гидроксид ионов, водородный и гидроксильный показатель для 2 М раствора уксусной кислоты, если K_д(СН₃СООН) = 1,75×10^-5.

Р е ш е н и е

Уксусная кислота – слабый электролит, диссоциирующий по схеме СН₃СООН Û СН₃СОО^– + Н⁺. K_д(СН₃СООН) << 1, поэтому для расчета степени диссоциации используем формулу (25)

a = 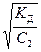= = 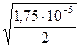2,96×10^-3 или 0,296 %

    Концентрацию ионов водорода найдем по уравнению (20)

[Н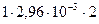⁺]  = = 5,92×10^-3 моль/дм³.

    Для определения концентрации ионов ОН^– формулу (38) преобразуем к виду

[ОН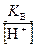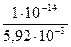^–] =  =  = 1,69∙10^-12 моль/дм³.

Водородный и гидроксильный показатели рассчитываем по формулам (39) и (41)

рН = –lg [Н⁺] = –lg(5,92×10^–3) = 2,23

рОН = 14 – рН = 14 – 2,23 = 11,77

 

Пример 2. Определите рН 0,017 М раствора муравьиной кислоты, если К_Д(НСООН) = 2·10^–4.

Р е ш е н и е

НСООН – слабая кислота, распадается на ионы по схеме НСООН Û НСОО^– + Н⁺,  поэтому расчет концентрации ионов Н⁺ ведем с использованием формул (25) и (20)

[Н⁺] = n × α· C₂ = n × .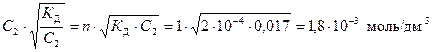

Водородный показатель рассчитываем по формуле (39)

рН = – lg 1,8 · 10^-3 = 2,75.

 

Пример 3. Определите рН в растворе Са(ОН)₂ с концентрацией 0,001 М.

Р е ш е н и е

Са(ОН)₂ – щелочь, по первой ступени степень диссоциации α = 1, а по второй ступени степень диссоциации незначительная, поэтому ею можно пренебречь. Тогда схему диссоциации данного сильного электролита следует представить таким образом

Са(ОН)₂ ® СаОН⁺ + ОН^–.

 Тогда [ОН^–] = [Са(ОН)₂] = 1×10^-3. Данный раствор является сильно разбавленным, поэтому при расчете  рОН можно использовать не активность, а концентрацию гидроксид-ионов. По уравнению (40)

рОН = – lg [ОН^–] = – lg(1×10^–3) = 3.

Из формулы (41) рН = 14 – рОН = 14 – 3 = 11.

 

Пример 4. Вычислите рН 0,1 М раствора азотной кислоты.

Р е ш е н и е

 Азотная кислота – сильная, в растворе практически полностью диссоциирует на ионы по схеме HNO₃ ® H⁺ + NO 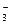. Степень диссоциации α ≈ 1, следовательно, [Н⁺] =[NO 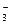] = С₂(НNO₃) = 0,1 моль/дм³. Поскольку концентрация кислоты достаточно велика, при расчете рН следует пользоваться активностью ионов водорода. Тогда по формуле (32)

I = ½ × (0,1·1² + 0,1 · 1²) = 0,1.

По уравнению (31 а) вычисляем коэффициент активности Н⁺

lg g₊ =  – 0,5×½(+1)²½× 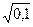 = –0,158; g₊ = 10^–0,158 = 0,695.

По формулам (26) и  (39)

а 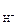 = [Н⁺] × g₊ = 0,1 ×0,695 = 0,0695 М.

рН = –lg а 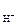= – lg 0,0695 = 1,16.

Пример 5. Рассчитайте молярную концентрацию раствора азотистой кислоты НNO₂, если  рН = 2,7.

Р е ш е н и е

Азотистая кислота – слабый электролит, диссоциирует по схеме

НNO₂ Û Н⁺ + NO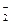

Из уравнения видно, что [Н⁺] = [NO 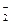]. Концентрации ионов найдем из формулы (39)

[Н⁺] = [NO 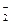] = 10^–рН = 10^–2,7 = 2×10^–3 моль/дм³.

Концентрация молекул кислоты, распавшихся на ионы, также составляет 2×10^–3 моль/дм³. Обозначив исходную концентрацию кислоты через С₂ и учитывая, что в начальный момент продуктов диссоциации не было, находим, что в состоянии равновесия концентрация недиссоциированных молекул кислоты  равна [НNO₂] = (С₂ − 2×10^–3) М.

    По формуле (22) константа диссоциации азотистой кислоты

.

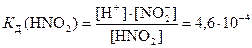Значение К_Д для азотистой кислоты взяли по справочнику [8]. Подставив в последнее выражение все известные концентрации, решаем уравнение относительно С₂

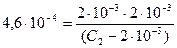; С₂ = 0,01 М.

 

Пример 6. Рассчитайте концентрацию основания Ва(ОН)₂ в растворе с рН = 11,3. Коэффициент активности γ (ОН⁻) = 0,965.

Р е ш е н и е

Ва(ОН)₂ – щелочь, сильный электролит, диссоциирует по схеме Ва(ОН)₂ → Ва²⁺ + 2ОН⁻. Из формулы (41)  

рОН = 14 – рН = 14 – 11,3 = 2,7.

Активность ионов ОН⁻ определим из уравнения (40)

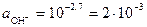моль/дм³.

 Из соотношения  (26) находим концентрацию ионов  ОН⁻ 

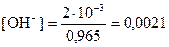 моль/дм³.

Из схемы диссоциации следует, что

С₂(Ва(ОН)₂) = 1/2×[ОН⁻] = 0,0021/2=0,00105 моль/дм³.

 

Пример 7. Рассчитайте рН буферного раствора, содержащего в 1 дм³ 0,1 моль СН₃СООН и 0,2 моль NaСН₃СОО. Оцените буферную ёмкость данного раствора по отношению к НСl.

Р е ш е н и е

По справочнику [8] находим значение константы диссоциации уксусной кислоты К_Д(СН₃СООН) = 1,75 · 10^–5.  Тогда

рК_Д(СН₃СООН) = –lgК_Д(СН₃СООН) = –lg(1,75 · 10^–5) = 4,757.

По формуле (43) определяем рН раствора

рН =  4,757 – lg 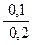 = 5,058.

При добавлении кислоты рН буферного раствора будет уменьшаться. Обозначим буферную ёмкость раствора по отношению к НСl через х моль. Тогда при добавлении х моль НСl к 1 дм³ раствора пойдет реакция

NaСН₃СОО + НСl = NaСl + СН₃СООН .

Концентрация СН₃СООН увеличится до (0,1 + х) моль/л, а концентрация NaСН₃СОО уменьшиться до (0,2 – х) моль/л.

    При добавлении НСl в количестве, равном буферной ёмкости раствора, рН понизится на единицу, т. е. будет равным 4,058. В этом случае из (39)

[Н⁺] = 10^–4,058 = 8,75·10^–5.

    По формуле (42)

[Н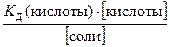⁺] =    или 8,75 · 10^-5 = ;

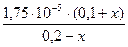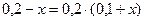; х = 6,67 моль/дм³.

Буферная ёмкость раствора по отношению к НСl равна 6,67 моль/л.    

                     

Пример 8. К 100 мл крови для понижения рН от 7,36 до 7,00 необходимо добавить 3,6 мл соляной кислоты с концентрацией 0,1 М. Чему равна буферная ёмкость крови по кислоте?

Р е ш е н и е

По формуле (45) найдем буферную ёмкость раствора по кислоте

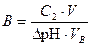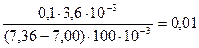=  моль/л.

                   

 

 

ПРОИЗВЕДЕНИЕ РАСТВОРИМОСТИ

     Краткие теоретические сведения

Для любого труднорастворимого электролита (Kt)_х(Аn)_у между его осадком и насыщенным раствором устанавливается равновесие вида

(Kt)_х(Аn)_у Û x ×Kt^{z +}  + y ×Аn^{z –}.

                                                                         ^{осадок                    насыщенный раствор}

Константа равновесия процесса диссоциации мало растворимого вещества в его насыщенном растворе называется произведением растворимости ПР.

Примеры решения задач

 

Пример 1. Вычислите произведение растворимости фторида кальция, если его растворимость в воде равна 0,024 моль/дм³.

Р е ш е н и е

Уравнение диссоциации имеет вид СаF₂↓Û  Са²⁺ + 2F ^–. Тогда по уравнению (48) равновесные концентрации ионов равны

[Са²⁺]= L;  [ F ^–]= 2× L .

По формуле (47)

ПР(СаF₂) = [Са²⁺]∙[ F ^–]² = L × (2 L)² = 4× L ³ = 4 × (0,024)³ = 5,53 × 10^-5.

Пример 2. Выпадет ли осадок йодида серебра при 25 °С после сливания 0,1 дм³ 0,005 М раствора нитрата серебра и 0,3 дм³ 0,002 М раствора иодида калия, если ПР(AgI)_табл = 1,1×10^-16?

Решение

При сливании указанных реактивов идет реакция

 

AgNO₃ + KI = AgI↓ + KNO₃ ,

Ag⁺ + I^– = AgI↓ .

Молярные концентрации ионов в растворах до смешивания равны

[Ag⁺] = 0,005 моль/дм³ ; [I^–] =0,002 моль/дм³.

Концентрации ионов в растворах после смешивания

[Ag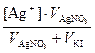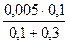⁺] = = = 1,25∙10^-3 моль/дм³; 

[I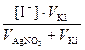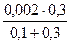^–] = = = 1,5∙10^-3 моль/дм³ .

По формуле (47) находим произведение концентраций ионов (ПР_расч)

ПР(AgI)_расч = [Ag⁺]×[I^–]= 1,25∙10^-3 ∙1,5∙10^-3 = 1,88×10^-6_.

AgI осаждается, так как соблюдается условие выпадения осадка

ПР(AgI)_расч > ПР(AgI)_табл .

Пример 3. Вычислите (не учитывая гидролиза) растворимость фосфата бария в моль/л и г/л, а также молярные концентрации ионов в насыщенном растворе данной соли, если ПР [Ва₃(РО₄)₂] = 6,3 · 10^-39.

Р е ш е н и е

Фосфат бария диссоциирует по схеме Ва₃(РО₄)₂↓↔ 3Ва²⁺ + 2РО 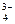, тогда по формуле (47)

ПР [Ва₃(РО₄)₂]  = [Ва²⁺]³ · [РО 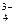]².

По уравнению (48) равновесные концентрации ионов равны

[Ва²⁺] = 3×L;       [РО 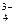] = 2×L .

Тогда по по формуле (50)   L = 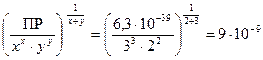 моль/л.

Молярная масса фосфата бария М₂(Ва₃(РО₄)₂) = 602 г/моль, тогда растворимость, выраженная в г/л

L = 602 · 9 · 10^-9 = 5,42 · 10^-6 г/л.

Концентрации ионов [Ва²⁺] = 3×L = 3 · 9 · 10^-9 = 2,7 · 10^-8 моль/л;

[РО 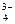] = 2×L = 9 · 10^-9 · 2 = 1,8 · 10^-8 моль/л.

Пример 4. Выпадет ли осадок галогенида серебра, если к 1 л  0,1 М раствора [Ag(NH₃)₂]NO₃, содержащему 1 моль аммиака добавить:

а) 1×10^–5 моль КВr;        б) 1×10^–5 моль КI.

Р е ш е н и е

Для решения вопроса о возможности разрушения комплексного иона за счет связывания комплексообразователя в малорастворимую соль необходимо оценить значения равновесных концентраций ионов в рассматриваемой системе. Для этого из справочника [8] выбираем значение константы нестойкости комплекса и произведения растворимости соответствующих солей

К_Н([Ag(NH₃)₂]⁺) = 5,9 · 10^–8;  ПР(AgBr) = 5,3 · 10^–13; ПР(AgI) = 8,3 · 10^–17.

    Данная комплексная соль диссоциирует по схеме

[Ag(NH₃)₂]NO₃ ® [Ag(NH₃)₂]⁺ + NO .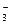

По определению для комплексного иона [Ag(NH₃)₂]⁺

К_Н([Ag(NH₃)₂]⁺) = .

[NH₃] ≈ С₂(NH₃) = 1 моль/л, так как концентрация молекул аммиака, образовавшихся вследствие вторичной диссоциации комплексного иона мала.

Из схемы первичной диссоциации следует, что

[[Ag(NH₃)₂]⁺] ≈ С₂([Ag(NH₃)₂]NO₃) = 0,1 моль/л.

Тогда концентрация ионов Ag⁺ равна

[Ag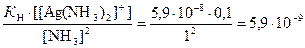⁺] = моль/л.

Концентрацию ионов Br ^–, достаточную для осаждения AgBr найдем из выражения для ПР (AgBr)

[Br 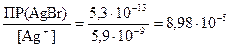^–] =  моль/л.

Так как необходимая для осаждения бромида серебра концентрация ионов брома ([Br ^–] = 8,98×10^–5 моль/дм³) больше добавляемой в составе бромида калия ([Br ^–] = 1×10^–5 моль/дм³), то осадок бромида серебра не выпадает.

Концентрацию ионов I^–, достаточную для осаждения AgI найдем по аналогии

[I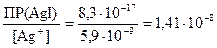^–] = моль/л.

Так как необходимая для осаждения йодида серебра концентрация ионов йода ([I ^–] = 1,41×10^–8 моль/дм³) меньше добавляемой в составе йодида калия ([I ^–] = 1×10^–5 моль/дм³), то реакция разрушения комплексного иона в данном случае будет протекать

[Ag(NH₃)₂]NO₃ + 2КI = AgI↓ + КNO₃ + 2NH₃ .

 

ГИДРОЛИЗ СОЛЕЙ

 

     Краткие теоретические сведения

 

Гидролизом соли называется взаимодействие ионов соли с молекулами воды, сопровождающееся изменением рН раствора. Гидролиз протекает только тогда, когда при взаимодействии ионов и воды образуются малодиссоциированные вещества. Известны следующие виды гидролиза солей.

1. Гидролиз по аниону.

В этом случае гидролизуются соли сильного основания и слабой кислоты, при этом реакция среды становится щелочной (рН > 7). Например

СН₃СООNa ® СН₃СОО ^– + Na⁺;

Na⁺ + HOH ® реакция практически не идет;

СН₃СОО ^– + HOH Û СН₃СООН + ОН ^–, рН > 7.

Молекулярное уравнение гидролиза

СН₃СООNa + HOH Û СН₃СООН + NaОН .

Если анион многозарядный, то гидролиз протекает ступенчато, например

Na₂CO₃ + HOH Û NaHCO₃ + NaOH;

 I ступень гидролиза: CO 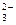 + HOH Û HCO  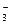+ OH ^–;

II ступень гидролиза: НCO 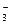 + HOH Û H₂CO₃ + NaOH .

Накапливающиеся в растворе ионы ОН ^– препятствуют протеканию II ступени гидролиза, поэтому практически гидролиз идет только по I ступени.

2.Гидролиз по катиону.

В этом случае гидролизуются соли слабого основания и сильной кислоты, при этом реакция среды становится кислой (рН < 7). Например

 (NH₄)₂SO₄ ® 2NH₄⁺ + SO ;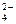

SO 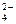 + HOH ® реакция практически не идет;

NH₄⁺ + HOH Û NH₄OH + H⁺, рН < 7.

Молекулярное уравнение гидролиза

(NH₄)₂SO₄ + HOH Û NH₄OH + NH₄HSO₄ .

Гидролиз не доходит до конца, так как накопление в растворе ионов водорода препятствует образованию свободной кислоты.

3. Гидролиз по катиону и аниону одновременно.

Такому виду гидролиза подвергаются соли слабого основания и слабой кислоты. В реакции участвуют и катион, и анион соли. Реакция среды определяется относительной силой образующихся слабой кислоты и слабого основания. Если K_Д (кислоты) > K_Д (основания), то рН < 7; если K_Д (кислоты)₎ < K_Д (основания), то рН > 7, а когда K_Д (кислоты) = K_Д (основания), то рН » 7. Например

NH₄COOH + HOH Û NH₄OH + HCOOH, рН = 7,

так как K_Д(HCOOH) = K_Д(NH₄OH) = 1,76 × 10^-5.

4. Необратимый полный гидролиз.

Если кислота и основание, образующие соль, являются не только слабыми электролитами, но и малорастворимы или неустойчивы и разлагаются с образованием газообразных продуктов, то гидролиз, как правило, протекает практически необратимо, например

Al₂S₃ + 6HOH ® 2Al(OH)₃¯ + 3H₂S ­;

2Al³⁺ + 3S^2– + 6HOH ® 2Al(OH)₃¯ + 3H₂S ­.

Количественно гидролиз соли характеризуется степенью гидролиза h и константой гидролиза K_г.

Степень гидролиза h показывает, какая часть соли находится в гидролизованном состоянии и выражается в долях единицы или в процентах

h = С_г / С₂ ,                                           (51)

где С_г – концентрация гидролизованной части соли; С₂ – общая концентрация растворенной соли.

Расчет константы гидролиза K_г и степени гидролиза h  следует вести по формулам:

1) гидролиз по аниону

K_г = 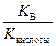,        h = 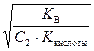 = 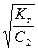,                           (52)

где K_{кислоты} – константа диссоциации слабой кислоты.

Если гидролиз протекает ступенчато, то в выражение для расчета константы гидролиза по первой ступени входит константа диссоциации слабого электролита по последней ступени.

Концентрация ионов ОН^–  и рН раствора соли могут быть вычислены по формулам

 [ОН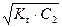^–] =  = h × С₂ ,                          (53)

рН = 14 – рОН = 14 + lg 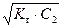.               (54)

 

2) гидролиз по катиону

K_г = 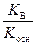,  h = 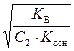 = 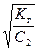,                            (55)

где K_осн – константа диссоциации слабого основания.

 [H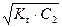⁺] =  = h × С₂ ,                                (56)

рН = –lg[H⁺] = –lg 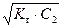.                             (57)

3) гидролиз по катиону и аниону одновременно:

K_г = 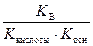 .                                        (58)

Для этого случая концентрация раствора соли практически не влияет на степень гидролиза

h = 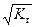.                                                  (59)

[H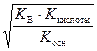⁺] =  ,                                            (60)

 рН = –lg 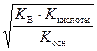.                                        (61)

 

 

Примеры решения задач

 

Пример 1. Определите характер среды водного раствора бората натрия.

Р е ш е н и е

Гидролиз соли, образованной сильным основанием NaOH и слабой многоосновной кислотой H₃BO₃ определяется ступенчатым характером диссоциации борной кислоты и обратного процесса – соединения ионов BO 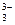 с ионами Н⁺.

Процесс гидролиза бората натрия можно выразить уравнениями:

I ступень: ВO 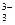 + HOH Û HВO 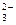+ OH^– ;

II ступень: НВO 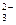 + HOH Û H₂ВO  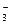+ OH^– ;

III ступень: H₂ВO 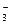 + НOH Û H₃BO₃ + OH^– .

Как правило, гидролиз заканчивается на I ступени. Тогда молекулярное уравнение гидролиза имеет вид:

Na₃BO₃ + HOH Û Na₂НBO₃ + NaOH, рН > 7(среда щелочная).

 

Пример 2. В какую сторону сместится гидролитическое равновесие при смешивании растворов карбоната натрия и сульфата алюминия?

Р е ш е н и е

Al₂(SO₄)₃ + 3Na₂CO₃ + 6HOH ® 2Al(OH)₃¯ + 3H₂O + 3CO₂­ + 3Na₂SO₄ .

В результате смешивания растворов катионы Н⁺, образующиеся при гидролизе Al₂(SO₄)₃, соединяются с анионами ОН^–, образующимися при гидролизе Na₂CO₃, что приводит к смещению равновесия реакции в сторону образования продуктов гидролиза. Смещение усиливается за счет разложения образующихся молекул Н₂CO₃ и выделения малорастворимого основания Al(OH)₃, поэтому реакция идет практически до конца. В ионной форме уравнение реакции имеет вид

2Al³⁺  + 3CO  + 6HOH ® 2Al(OH)₃¯ + 3H₂O + 3CO₂­

Пример 3. Вычислите константу гидролиза, степень гидролиза и рН    0,02 М раствора СН₃СООK. К_Д(СН₃СООН) = 1,8 · 10^–5.

Р е ш е н и е

Соль СН₃СООK образована сильным основанием КОН и слабой кислотой СН₃СООН. Ионное уравнение гидролиза имеет вид

СН₃СОО^– + НОН Û СН₃СООН + ОН^– .

    Для расчета константы и степени гидролиза используем формулу (52)

K_г = 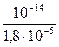 = 5,56×10^-10;

 h = 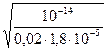 = 1,67×10^-4.

 

Пример 4. Вычислите константу гидролиза, степень гидролиза и рН 0,2 М раствора K₃PO₄, если константы диссоциации ортофосфорной кислоты по первой, второй и третьей ступеням соответственно равны

К_I  = 7,5∙10^–3; К_II = 6,25∙10^–8; К_III = 2,2∙10^–13 .

Р е ш е н и е

Соль K₃PO₄ образована сильным основанием КОН и слабой кислотой H₃PO₄. Так как гидролиз преимущественно протекает по первой ступени, тогда молекулярное и ионное уравнение гидролиза имеют вид

K₃PO₄ + Н₂O Û K₂HPO₄ + KОН

PO₄^3– + Н₂O Û HPO₄^2– + ОН^–

Для расчета константы гидролиза берем константу диссоциации ортофосфорной кислоты по третьей ступени

K_г = 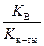 =  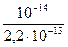= 4,55×10^–2.

Степень гидролиза рассчитываем по формуле (52)

 h = 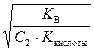 =  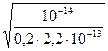= 0,477.

Концентрацию гидроксид ионов оценим по уравнению (53)

[ОН^–] = h × С₂ = 0,477×0,2 = 9,53×10^–2.    

рН раствора вычислим по формуле (54)

рН = 14 + lg 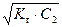 = 14 + lg  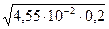= 12,98.

 

 

Список литературы

 

1. Павлов Н.Н. Общая и неорганическая химия: Учеб. для вузов. – М.: ООО «Дрофа», 2002.

2. Общая химия в формулах, определениях, схемах / И.Е. Шиманович, М.Л. Павлович, В.Ф. Тикавый, П.М. Малашко; Под ред. В.Ф. Тикавого. – Мн.: Унiверсiтэцкае, 1996.

3. Задачи по общей и неорганической химии: Учеб. пособие для студентов высш. учеб. заведений / Р.А. Лидин, В.А. Молочко, Л.Л. Андреева; Под ред.
Р.А. Лидина. – М.: Гуманитар. изд. центр ВЛАДОС, 2004.

4. Задачи и упражнения по общей химии: Учеб. пособие / Б.И. Адамсон, О.Н. Гончарук, В.Н. Камышова и др.; Под ред. Н.В. Коровина. – М.: Высш. шк., 2003.

5. Сборник задач и упражнений по общей химии: Учеб. пособие / С.А. Пузаков, В.А. Попоков, А.А. Филиппова. – М.: Высш. шк., 2004.

6. Сборник задач и упражнений по общей химии: Учеб. пособие для нехим. спец. вузов / Л.М. Романцева, З.И. Лещинская, В.А. Суханова. – 2-е изд., перераб. и доп. – М.: Высш. шк., 1991.

7. Глинка Н.Л. Задачи и упражнения по общей химии: Учеб. пособие для вузов. – М.: Интеграл-Пресс, 2001.

8. Рабинович В.А., Хавин З.Я. Краткий химический справочник. – Л.: Высш. шк., 1991.

9. Литвинова Т. Н., Сборник задач по общей химии: Учеб. пособие для вузов. – 3-е изд., перераб. - М.: ООО «Издательство Оникс»: ООО «Издательство «Мир и Образование», 2007. – 224 с.

Содержание

 

Введение ....................................................................................................      3

Растворимость. Способы выражения состава растворов ......................      3

Краткие теоретические сведения ...........................................................      3

Примеры решения задач .......................................................................     6

Разбавленные растворы неэлектролитов .................................................     11

Краткие теоретические сведения ...........................................................     11

Примеры решения задач .......................................................................     13

Растворы электролитов ............................................................................     15

Краткие теоретические сведения ...........................................................     15

Примеры решения задач .......................................................................     18

Ионное произведение воды. Буферные растворы ...................................     21

Краткие теоретические сведения ...........................................................     21

Примеры решения задач .......................................................................     22

Произведение растворимости ..................................................................     26

Краткие теоретические сведения ...........................................................     26

Примеры решения задач .......................................................................     27

Гидролиз солей .........................................................................................     30

Краткие теоретические сведения ...........................................................     30

Примеры решения задач .......................................................................     32

Литература ................................................................................................     34

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОУ ВПО ЧЕРЕПОВЕЦКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

 

 

Факультет общих математических и естественнонаучных дисциплин

Кафедра химии

 

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

ПО  ДИСЦИПЛИНЕ

«ОБЩАЯ И НЕОРГАНИЧЕСКАЯ ХИМИЯ»

 

(Для студентов заочной формы обучения)

Часть 3

Учебно-методическое пособие

 

 

                                                       Специальности:    240301   Химическая технология

                                                        неорганических веществ;   280201 Охрана окру-

                                                           жающей  среды  и  рациональное  использование

                                                           природных ресурсов; 240801 Машины и аппара-

                             ты химических производств

 

 

Череповец

2007

 

 

Примеры решения задач по дисциплине «Общая и неорганическая химия» для студентов заочной формы обучения: В 3 ч. Ч. 3: Учеб.-метод. пособие. – Череповец: ГОУ ВПО ЧГУ, 2007. – 35 с.

 

 

Рассмотрено на заседании кафедры химии, протокол №  9 от 14.05. 07.

Одобрено редакционно-издательской комиссией факультета общих математических и естественнонаучных дисциплин ГОУ ВПО ЧГУ, протокол №  8 от 15.05. 07.

 

Составители:   О.А. Калько – канд. техн. наук, доцент;              

                      Ю.С. Кузнецова;

Н.В. Кунина

                          

 

Рецензенты:  С. Н. Балицкий  – канд. хим. наук, доцент (ГОУ ВПО ЧГУ);

                 Л.Ю. Кудрявцева – канд. техн. наук, доцент (ГОУ ВПО ЧГУ)

                      

 

 

Научный редактор: Г.А. Котенко – канд. хим. наук, профессор

 

 

                                                      © Калько О.А., Кунина Н.В.,

                                                           Кузнецова Ю.С., 2007

                                                      ©ГОУ ВПО Череповецкий государст-­

                                                                  венный  университет, 2007

 

ВВЕДЕНИЕ

Данное учебно-методическое пособие содержит краткие теоретические сведения и примеры решения задач по теме «Растворы» курса «Общая и неорганическая химия». Пособие предназначено для студентов заочной формы обучения в качестве вспомогательного руководства для самостоятельной работы при выполнении домашних контрольных работ. Содержание учеб­но-методического пособия соответствует государственному стандарту дисциплины «Общая и неорганическая химия» для химических специальностей.

 

 

РАСТВОРИМОСТЬ. СПОСОБЫ ВЫРАЖЕНИЯ

СОСТАВА РАСТВОРОВ