у

                          Положительная

                   х

у                        Аналитическая. Коэф. коррел. стрем-ся к 1

                          r стрем-ся к 1. 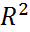à1

                   х

у                        Коэф. детерминации. стрем-ся к 0, r к -1

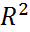                          à1

                   х

у                        Стохастическая.    

                   х 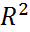                                       à0, rà0

Ковариационный анализ (ANCOVA).

Ковариаты:-Фиксированные, -Переменные

Коэффициент ковариации (корреляционный момент)

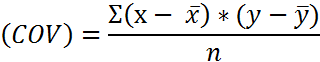
Билет № 8. Приведите классификацию аналитических характеристик тесноты линейной и нелинейной взаимосвязи отклика с одним, двумя и несколькими факторами.

Аналитические характеристики делятся на:

- с помощью порядковых статистик;

- ранговая корреляция;

- точечно-бисериальная корреляция;

Наиболее часто используемые:

- коэффициенты ковариации;

- коэффициенты корреляции (для парной, множественной и частной корреляции);

- корреляционное отношение (для криволинейной связи случайных величин);

- коэффициенты детерминации;

- Q - коэффициенты (редко применяются в технике).

Если коэфф. корреляции между фактором и откликом высокий – это предполагает влияние достоверного статистического влияния данного фактора.

Если коэф.корреляции высокий между двумя факторами – это говорит о наличии явления мултиколлинеарности (наличие линейной зависимости между объясняющими переменными (факторами) регрессионной модели).

Билет № 9. Какие аналитические характеристики тесноты взаимосвязи двух случайных величин Вы знаете? Приведите формулы их определения. Как эти характеристики определяются в рамках программы MS Excel.

Наиболее часто используемые аналитические характеристики «тесноты» связи делятся на следующие виды:

- коэффициенты ковариации;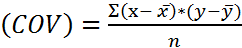

- коэффициенты корреляции (для парной, множественной и частной корреляции) ;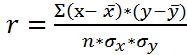

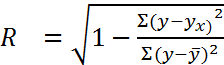
- корреляционное отношение (для криволинейной связи случайных величин);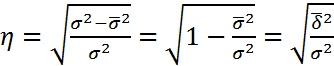

- коэффициенты детерминации;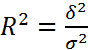

- Q - коэффициенты (редко применяются в технике).

Функции КОВАР и КОРРЕЛ определяют соответственно коэффициенты ковариации и корреляции, функция ПИРСОН.

В MS EXCEL имеются также инструменты анализа «Ковариация» и «Корреляция», сходные своими диалоговыми окнами. Они служат длятой же цели, что и соответствующие функции, но в отличие от функций в данном случае задаётся общий входной интервал с разделением анализируемых переменных по строкам или столбцам.

Билет № 10. При изменении режимов обработки контролировали значения подачи (2, 3, 4 и 5 мм/мин) и соответствующие значения усилия резания (150, 250, 340 и 420 кн). Как Вы будете рассчитывать коэффициент корреляции между этими параметрами, оценивать степень корреляционной связи и проверять значимость коэффициента корреляции?

Коэффициент корреляции считается по формуле:

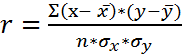 (линейный);

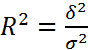 (множественный).

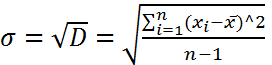(средний квадрат отклонений от среднего). Если коэф. корреляции близок к 1, то модель достаточно достоверна.

Билет № 11. Как связаны коэффициент детерминации (R²) и коэффициент корреляции (r), корреляционное отношение (ню?)? Чем обусловлена эта связь?

Чем больше совместное отклонение x и y от их средних значений, тем больше |r|. Деление на σ_Х и σ_y делает r безразмерным.

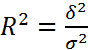- коэффициент детерминации,

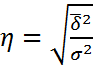- корреляционное отношение;

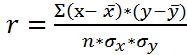 - коэффициент корреляции.

Билет № 12. Для характеристики силы связи между какими случайными величинами используется понятие «ранговой корреляции»? Как наиболее просто определить «тесноту» связи между этими случайными величинами? Какие «специализированные» коэффициенты ранговой корреляции Вы знаете?