Билет № 5. Как Вы представляете сущность корреляционного, дисперсионного и регрессионного анализов? Как, по Вашему мнению, они взаимосвязаны? Нарисуйте схему основных этапов исследования статистических зависимостей.
Корреля́ционный анализ устанавливает насколько тесно связаны случайные величины.
Дисперсионный анализ устанавливает существенное колебание одной или нескольких независимых случайных величин и их взаимодействия на дисперсную зависимость случайных велин.
Регрессионный анализ - статистический метод исследования влияния одной или нескольких независимых переменных 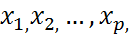 на зависимую переменную y.
на зависимую переменную y.
Этапы построения регрессионной модели:
 |







 | |||||||||
 |  | ||||||||
 | |||||||||
 | |||||||||
1-выбор независимых и зависимых случ. величин и числа опытов.
2-инф.этап, провод. активный или пассивный эксперимент.
3-корреляционный и дисперсионный анализ
4-этап параметрической модели
5-анализ мультиканальности и отбор сущ.фактов.
6-выч. коэф.регрессии
7-анализ точности и дост. точности получ. модели.
Билет № 6. Какие способы оценки тесноты взаимосвязи двух случайных величин Вы знаете? Приведите примеры.
Характеристики "тесноты" статистической связи:
1) Табличная (корреляционная матрица)
Графическая (корреляционный график)
3) Аналитические:
а) Ковариационный анализ (ANCOVA).
Ковариаты:-Фиксированные, -Переменные
Коэффициент ковариации (корреляционный момент)
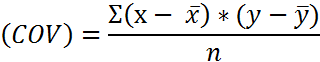
б) Коэффициент корреляции (прямолинейная связь):
-Простой (r, 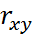 ) (парный, линейный)
) (парный, линейный) 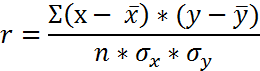
-Множественный (коэф. коррел-ии R)
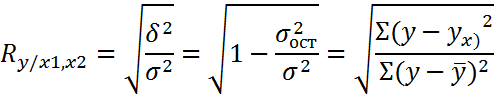
где 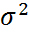 -общая дисперсия Y,
-общая дисперсия Y,
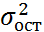 – остаточная дисперсия,
– остаточная дисперсия,
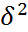 – дисперсия теоретических значений Y, рассчитанная по уравнению регрессии,
– дисперсия теоретических значений Y, рассчитанная по уравнению регрессии,
R для 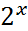 факторов (через парные r)
факторов (через парные r)

-Частные. Отражает связь между двумя величинами при фиксированных значениях других ( 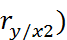
в) Корреляционное отношение, индекс корреляции (криволинейная связь):
-Эмпирическое 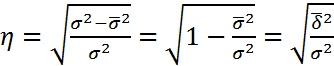
-Теоретическое 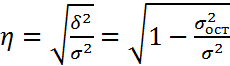
δ^2-характеризует отклонение групповых средних от общей средней.
г) Коэффициент детерминации:
-Частный ( 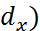
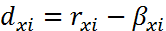
где 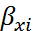 - коэф. уравнения множественной регресии, показывает на сколько % вариация результативного признака объясняется вариацией
- коэф. уравнения множественной регресии, показывает на сколько % вариация результативного признака объясняется вариацией 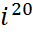 фактора
фактора
-Множественный ( 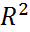 ) Доля вариации результативного признака, обусловленная изменением факторов
) Доля вариации результативного признака, обусловленная изменением факторов 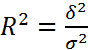
д) Q – коэффициент. 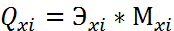 ,
,
где 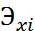 – коэф. эластичности
– коэф. эластичности
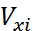 – коэф. вариации i^20 фактора.
– коэф. вариации i^20 фактора.
Билет № 7. Изобразите графические примеры «тесной» (аналитической и стохастической) и слабой связи двух случайных величин; положительной и отрицательной корреляции.
Билет № 10. При изменении режимов обработки контролировали значения подачи (2, 3, 4 и 5 мм/мин) и соответствующие значения усилия резания (150, 250, 340 и 420 кн). Как Вы будете рассчитывать коэффициент корреляции между этими параметрами, оценивать степень корреляционной связи и проверять значимость коэффициента корреляции?
Коэффициент корреляции считается по формуле:
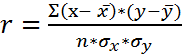 (линейный);
(линейный);
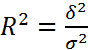 (множественный).
(множественный).
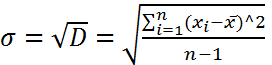 (средний квадрат отклонений от среднего). Если коэф. корреляции близок к 1, то модель достаточно достоверна.
(средний квадрат отклонений от среднего). Если коэф. корреляции близок к 1, то модель достаточно достоверна.
Билет № 11. Как связаны коэффициент детерминации (R2) и коэффициент корреляции (r), корреляционное отношение (ню?)? Чем обусловлена эта связь?
Чем больше совместное отклонение x и y от их средних значений, тем больше |r|. Деление на σХ и σy делает r безразмерным.
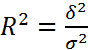 - коэффициент детерминации,
- коэффициент детерминации,
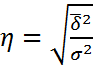 - корреляционное отношение;
- корреляционное отношение;
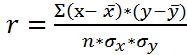 - коэффициент корреляции.
- коэффициент корреляции.
Билет № 12. Для характеристики силы связи между какими случайными величинами используется понятие «ранговой корреляции»? Как наиболее просто определить «тесноту» связи между этими случайными величинами? Какие «специализированные» коэффициенты ранговой корреляции Вы знаете?
Форму связи, Вы знаете?
Регрессионный анализ.
В широком понятии этого слова регрессионный анализ состоит из трёх основных тесно взаимосвязанных компонентов: корреляционного, дисперсионного и собственно регрессионного анализов
Задачи пэ:
1) Поиск оптимальных условий, обеспечивающих наилучшую реализацию процесса.
2) Построение интерполяционных формул.устанавливающих количественную связь м/д значением выходного параметра и фактором от которых он зависит, это интерполяционный эксперимент.
Требования к объектам исследования:
1. Воспроизводимость.
2. Управляемость.
Требования к параметрам оптимизации:
1. Должны иметь физический смысл.
2. Легко вычисляются.
3. Всегда задаются числом.
4. Должны быть одинаковыми.
5. Должны быть универсальными и полными.
Требования к исследуемым факторам:
1. Необходимость контроля и учета всех факторов.
2. Управляемость.
3. Совместность.
4. Независимость (ортагональность факторов).
Билет № 20. Этапы планирования эксперимента. Матрица планирования полного факторного эксперимента.
Этапы планирования эксперимента:
1. Выбор центроплана.
2. Выбор оптимальной величины варьирования.
3. Преобразование значений управляемых переменных (учитывающих в эксперименте).
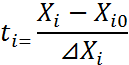
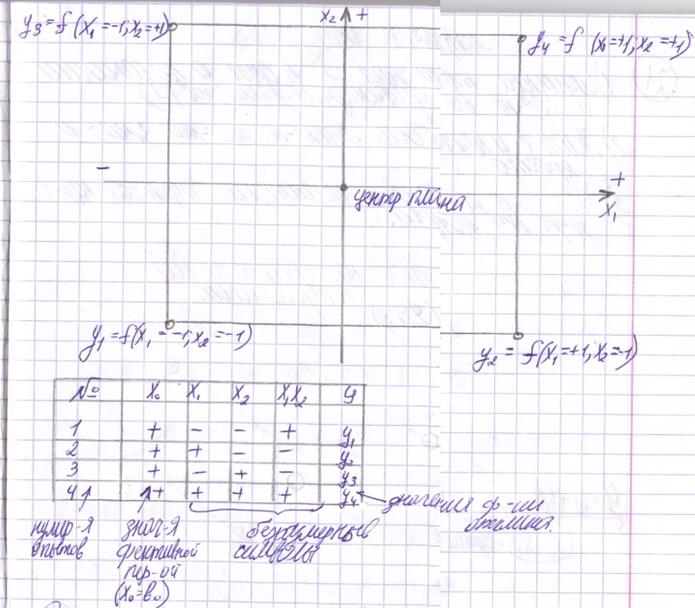
План эксперимента задается в виде матрицы планирования:

Билет № 5. Как Вы представляете сущность корреляционного, дисперсионного и регрессионного анализов? Как, по Вашему мнению, они взаимосвязаны? Нарисуйте схему основных этапов исследования статистических зависимостей.
Корреля́ционный анализ устанавливает насколько тесно связаны случайные величины.
Дисперсионный анализ устанавливает существенное колебание одной или нескольких независимых случайных величин и их взаимодействия на дисперсную зависимость случайных велин.
Регрессионный анализ - статистический метод исследования влияния одной или нескольких независимых переменных 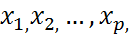 на зависимую переменную y.
на зависимую переменную y.
Этапы построения регрессионной модели:
 |







 | |||||||||
 |  | ||||||||
 | |||||||||
 | |||||||||
1-выбор независимых и зависимых случ. величин и числа опытов.
2-инф.этап, провод. активный или пассивный эксперимент.
3-корреляционный и дисперсионный анализ
4-этап параметрической модели
5-анализ мультиканальности и отбор сущ.фактов.
6-выч. коэф.регрессии
7-анализ точности и дост. точности получ. модели.
Билет № 6. Какие способы оценки тесноты взаимосвязи двух случайных величин Вы знаете? Приведите примеры.
Характеристики "тесноты" статистической связи:
1) Табличная (корреляционная матрица)
Графическая (корреляционный график)
3) Аналитические:
а) Ковариационный анализ (ANCOVA).
Ковариаты:-Фиксированные, -Переменные
Коэффициент ковариации (корреляционный момент)
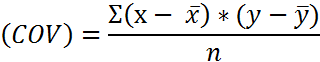
б) Коэффициент корреляции (прямолинейная связь):
-Простой (r, 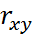 ) (парный, линейный)
) (парный, линейный) 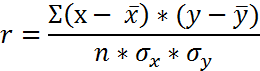
-Множественный (коэф. коррел-ии R)
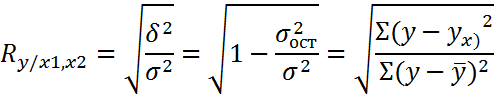
где 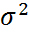 -общая дисперсия Y,
-общая дисперсия Y,
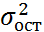 – остаточная дисперсия,
– остаточная дисперсия,
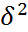 – дисперсия теоретических значений Y, рассчитанная по уравнению регрессии,
– дисперсия теоретических значений Y, рассчитанная по уравнению регрессии,
R для 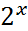 факторов (через парные r)
факторов (через парные r)

-Частные. Отражает связь между двумя величинами при фиксированных значениях других ( 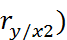
в) Корреляционное отношение, индекс корреляции (криволинейная связь):
-Эмпирическое 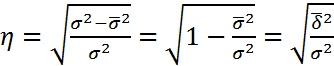
-Теоретическое 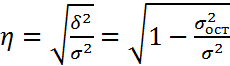
δ^2-характеризует отклонение групповых средних от общей средней.
г) Коэффициент детерминации:
-Частный ( 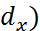
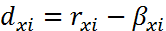
где 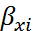 - коэф. уравнения множественной регресии, показывает на сколько % вариация результативного признака объясняется вариацией
- коэф. уравнения множественной регресии, показывает на сколько % вариация результативного признака объясняется вариацией 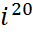 фактора
фактора
-Множественный ( 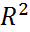 ) Доля вариации результативного признака, обусловленная изменением факторов
) Доля вариации результативного признака, обусловленная изменением факторов 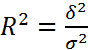
д) Q – коэффициент. 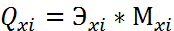 ,
,
где 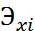 – коэф. эластичности
– коэф. эластичности
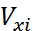 – коэф. вариации i^20 фактора.
– коэф. вариации i^20 фактора.
Билет № 7. Изобразите графические примеры «тесной» (аналитической и стохастической) и слабой связи двух случайных величин; положительной и отрицательной корреляции.
Дата: 2019-02-02, просмотров: 333.