Составной частью изучения учебного курса «Основы телекоммуникаций» является выполнение студентами - заочниками письменной контрольной работы.
Для подготовки к контрольной работе необходимо изучить теоретический материал, выполнить рекомендации и задания для самостоятельной работы.
Контрольная работа выявляет приобретенные студентами знания по определенной учебной теме, показывает умение правильно формировать и обосновывать теоретические положения, кругозор студента, его начитанность. Студенческая контрольная работа дает возможность судить о том, как усвоил студент ту или иную тему курса, насколько глубоко и правильно разобрался в рекомендованной литературе, умеет ли излагать полученные знания, применять теоретический материал для решения практических задач и умение делать выводы по итогам решения. Кроме того, контрольная работа показывает, какие пробелы имеются в знаниях студента по данной теме, какие допущены ошибки.
Чтобы контрольная отвечала предъявленным требованиям, автор должен обнаружить знания по всей теме, а не только по одному из ее разделов.
Контрольное задание состоит из трех вопросов и составлено для десяти вариантов.
Первое задание всех десяти вариантов относится к разделу 1, второе, третье задание соответствует второму разделу программы.
Прежде чем приступить к выполнению контрольного задания, ознакомьтесь с порядком выбора варианта и требованиями к оформлению контрольной работы.
Контрольное задание составлено в 10 вариантах. Выбор варианта осуществляется в соответствии с номером, под которым записана фамилия студента в журнале учебной группы: последняя цифра номеров с 1 по 9 обозначает соответственно номер 1,2,3,4,5,6,7,8,9 варианта контрольной работы; цифре 0 соответствует 10 варианту.
Внимательно изучите указания по оформлению контрольной работы. Выполнение этих требований обязательно.
Указания по оформлению домашней контрольной работы.
Работа должна быть аккуратно оформлена. При оформлении необходимо придерживаться следующих правил:
- контрольные работы выполняются в тетради в клетку, с
отчерченными полями, все страницы должны быть пронумерованы в
верхнем углу;
- последовательность заполнения тетради: условие задания 1(пол-
ностью) - ее решение, условие задания 2 - ее решение и т.д.;
- после записи условия задачи приводятся расчеты, схемы, а также
рисунки, графики и т.п., которые должны вычерчиваться остро
заточенным карандашом, аккуратно в достаточно крупном масштабе; не
допускается использование ксерокопий;
-рисунки должны сопровождаться порядковым номером и
соответствующей подрисуночной надписью, нумерация рисунков
сквозная;
-после выполнения всех заданий приводится список используемой литературы с указанием издательства и года издания, личная подпись и дата выполнения работы;
-работа высылается на рецензирование в соответствии с учебным графиком; после получения зачтенной работы Вы должны внести исправления в соответствии с рецензией и показать их преподавателю во время экзаменационной сессии, но до зачета.
ЗАДАНИЯ НА КОНТРОЛЬНУЮ РАБОТУ
Задание №1
Проанализировать граф сети, составить матрицы связности, инцидентности для ориентированного и неориентированного графа.
Порядок выполнения:
1. Написать определение графа сети.
2. Вычертить граф сети согласно своего варианта, пронумеровать вершины, ребра.
3. Составить матрицы связности, инцидентности.
4. Разработать граф сети из 8 вершин, пронумеровать вершины, ребра.
5. Составить матрицы связности, инцидентности для графа из 8 вершин.
Исходные данные:
Дано модельное представление сети связи как объект и анализа.
Методический материал и пример выполнения задания №1
Сеть связи (телекоммуникационная связь) как объект синтеза и анализа представляет собой совокупность пунктов сети и соединяющих их линий. В качестве математической модели такого объекта используется граф.
Графом называется некоторая совокупность точек и связывающих их линий.
Точка графа называются вершинами, а линии – дугами. Граф математически обозначается как G(N,V), где N – конечное множество вершин мощностью n,а V-конечное множество дуг мощностью m.
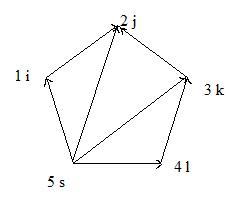
Рисунок 1 - Ориентированный граф
Вершины можно обозначить строчными буквами(i,j,k,l,s) либо цифрами (1,2,3,4,5) (рисунок 1 ), а дуги соответственно парами {(i,j),(j,k),(k,l)…} либо {(1,2),(2,3),(3,4),…}, где первый индекс определяет начало, а второй –конец дуги.
Граф, в котором задается направление дуг, называется ориентированным (Б), а в противном случае – неориентированным (А). Неориентированные дуги называются ребрами.
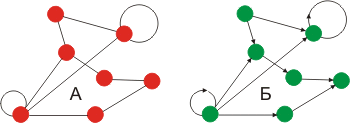
Между двумя вершинами, соединенными дугой (ребром), существует отношение смежности (для ориентированного графа вершины I и j смежны, если дуга начинается в i и направлена в j).
Между вершиной и соединенными с ней дугами( ребрами) существует отношение инцидентности.
Граф, каждой дуге(ребру) которого поставлены в соответствие некоторых числовых характеристик, называемые весами, представляет собой взвешенный граф. При необходимости веса могут быть приписаны также вершинам графа.
Взвешенный граф принято называть сетью ( в данном случае имеется в виду сетевая модель, а не сама сеть). Весовыми характеристиками сети могут быть расстояния, пропускная способность, стоимость и т.д.
Помимо геометрического изображения в виде точек и линий, граф может быть представлен в дискретной форме. Именно эта форма используется при вводе графовой модели ЭВМ.
Одним из наиболее распространенных дискретных представлений графа является матрица смежностей. Эта матрица A=[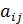 
] размером n x n элементов, которые могут принимать значения:
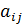= 1, если в графе G существует дуга (ребро) между вершинами i и j;
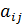= 0, в противном случае.
Матрица смежностей графа, приведенного на рисунке 1, имеет вид
A =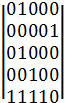 
Для хранения матрицы сменности в памяти ЭВМ, как видим, необходимо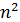 
ячеек. У неориентированного графа матрица смежности симметрична главной диагонали, и, следовательно, в памяти может храниться лишь один её треугольник, что позволяет экономить память, но усложняет ее работу на ЭВМ.
Если перенумеровать в произвольном порядке дуги (ребра) графа G и поставить эти номера в соответствие номерам строк некоторой матрицы B=[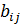 
], а номера столбцов оставить по-прежнему соответствующим номерам вершин графа, то такой матрице можно отобразить отношение инцидентности элементов графа G. Элементы матрицы 
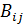могут принимать значения {0,1}.
Перенумеруем дуги для рассматриваемого графа: (I,j)-1; (j,k)- 2; (k,l)-3; (l,s)—4; (s,i)-5; (s,j)-6; (s,k)-7. Тогда матрица инцидентности будет иметь вид:
B= 
Задание №2
Осуществить процедуру кодирования сигналов в системе связи с ИКМ.
Порядок выполнения:
1. Вычертить схему кодера взвешивающего типа.
2. Выполнить кодирование отсчетов согласно вариантам заданий, приведенным в таблице 1.
Исходные данные
Таблица 1
| № варианта | Амплитуда АИМ-сигнала IАИМ, Δ |
| 1 | 85,1; -34,8; 40,5; 82,7; -92,3; -70,4; 101,8 |
| 2 | -47,2; 33,3; 61,8; -75,5; -97,6; 99,9; 106,0 |
| 3 | -39,8; 42,2; 59,7; -77,6; -81,3; -98,6; -102,5 |
| 4 | 44,4; -53,2; 69,4; -78,3; 89,1; -93,8; 110,7 |
| 5 | 49,2; 57,6; -88,9; 95,4; 109,6; -64,3; -118,7 |
| 6 | -31,5; -45,2; -60,9; 74,5; 80,9; 96,1; 115,3; |
| 7 | 35,6; -51,9; 67,8; -72,4; 85,6; -94,3; 108,1; |
| 8 | 38,4; -56,2; -68,9; -79,4; -86,3; 97,4; 103,6; |
| 9 | -48,5; -52,9; 65,3; 71,2; 83,4; 90,6; -112,3 |
| 10 | 41,5; 58,9; -62,7; -73,6; 82,9; -91,3; -111,4 |
3. Результаты поэтапного кодирования первого амплитудного отсчета занесите в таблицу 2.
Таблица 2
| Такты (разряды) кодиро- вания |
IЭТ |
IАИМ - IЭТ | Состояние выхода компара- тора «0» или «1» | Выходы ЛУ | |
| Состояние ключей ГЭТ «вкл» («выкл») | Запись решения | ||||
| 1 | 0 | ||||
| 2 | 64 | ||||
| 3 | 32 | ||||
| 4 | 16 | ||||
| 5 | 8 | ||||
| 6 | 4 | ||||
| 7 | 2 | ||||
| 8 | 1 | ||||
SКВ = │IАИМ│- ∑│IЭТ│
4. Определить ошибку квантования.
5. Результаты кодирования остальных отсчетов занесите в таблицу 3
Таблица 3
| Амплитудный отсчет IАИМ | 7-разрядная кодовая комбинация | Ошибка квантования |
Методический материал и пример выполнения задания №2
Принцип работы кодера заключается в уравновешивании кодируемых отсчетов эталонными токами или просто эталонами с определенными весами (значениями) Кодирование в этом случае можно представить как процесс поэтапного взвешивания на чашечных весах, снабженных указателями «больше-меньше». На одну чашу весов помещается кодируемый отсчет, а на другую последовательно устанавливают эталоны, начиная с большего веса. На каждом из этапов (тактов) взвешивания по указателю «больше-меньше» принимают соответствующее решение. По окончании взвешивания отсчет будет уравновешен эталонами, сумма которых с точностью до эталона наименьшего веса будет равна «весу» отсчета. Значение эталона наименьшего веса и будет максимально возможной ошибкой квантования.
Принцип построения кодера с линейной шкалой квантования показан на рисунке 2.
Рассмотрим принцип работы кодера.
Кодер содержит компаратор КЭ генератор эталонных токов ГЭТ, логическое устройство ЛУ, преобразователь кода ПК.
Компаратор (указатель «больше-меньше») определяет знак разности между амплитудами токов кодируемого сигнала и суммой эталонных токов IАИМ - IЭТ. Если в момент такта кодирования IАИМ - IЭТ >0, т.е. IАИМ >IЭТ, то на выходе компаратора формируется 0 (пробел). Если IАИМ<IЭТ, то формируется 1 (импульс).
ЛУ служит для записи решений компаратора после каждого такта кодирования и управления работой ключей Кл1-Кл7.
Преобразователь кода ПК преобразует параллельный код в последовательный, формируя выходной ИКМ сигнал. Управление работой узлов кодера осуществляется сигналами, поступающими от генераторного оборудования ГО системы передачи.
Если шаг линейного квантования Δ, тогда значения эталонных токов будут Δ, 2Δ, 4Δ,…., 2m-1Δ, где m – разрядность кодовой комбинации. Структура кодовой группы формируется на выходах 1, 2,…, m логического устройства.
Перед началом кодирования все выходы ЛУ устанавливаются в состояние 0. В моменты, предшествующие такту кодирования, выходы Лу последовательно, начиная с первого, переводятся в состояние 1. Решение компаратора это состояние сохраняет, если в момент такта кодирования на его выходе формируется 0; если на выходе компаратора формируется 1, выход ЛУ переводится в 0. Состояние выхода ЛУ, отмеченное как 1, означает замыкание соответствующего ключа или подключение эталонного тока определенного веса в точку суммирования эталонных токов (вход 2 компаратора). Состояние 1 первого выхода ЛУ замыкает Кл.1, второго выхода – Кл.2 и т.д.
Работу кодера можно пояснить на примере кодирования отрицательного отсчета с амплитудой IАИМ = -105,3Δ. Кодирование такого отсчета производится 1-разрядной кодовой группой, что позволяет закодировать 128 уровней. Для этого используются 7 эталонных токов с условными весами Δ, 2Δ, 4Δ, 8Δ,…, 64Δ.
Дата: 2019-02-02, просмотров: 587.
