Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

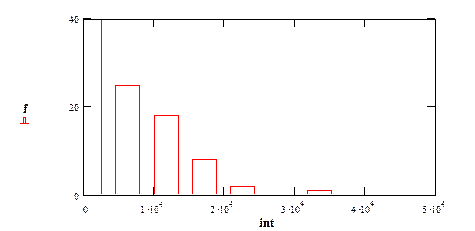
Рис.9. Гистограмма

 

 

Проверка статистических гипотез:

 

Гипотеза №1: Распределение исходных данных о наработке до отказа соответствует экспоненциальному закону.

 

Число отказов при зафиксированных наработках объектов в случае экспоненциального закона распределения равно:

;

;

;

;

;

;

;

;

;

;

;

;

;

.

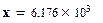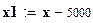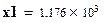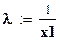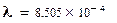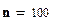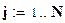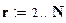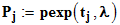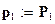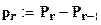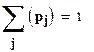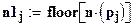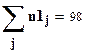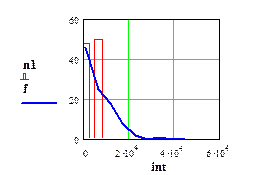
Рис. 10. Гистограмма частот отказов при экспоненциальном законе распределения и полигон частот исходной выборки

Параметр экспоненциального закона в данном случае откорректирован путём уменьшения математического ожидания "x" исходной выборки.

Критерий Хи-квадрат Пирсона при гипотезе экспоненциального закона распределения наработок до отказа:

;

.

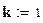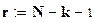Число степеней свободы

.

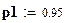Доверительная вероятность

;

.

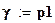 Квантиль Хи-квадрат распределения при вероятности 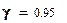и числе степеней свободы 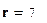равна .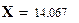 

;

;

.

 

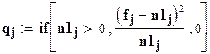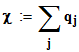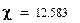 Вывод. Сравнение вычисленного значения критерия 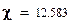 и значения квантили 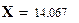показывает, что вычисленное значение меньше. Это позволяет сделать вывод о том, что гипотеза экспоненциального закона распределения наработок до отказа может быть принята с доверительной вероятностью 0,95.

Гипотеза №2. Распределение исходных данных о наработке до отказа соответствует нормальному закону .

 

Число отказов при зафиксированных наработках объектов при нормальном законе распределения равно:

;

;

;

.

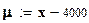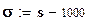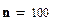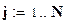Статистические оценки математического ожидания "x" и среднеквадратического отклонения "s" корректируются для получения согласия с проверяемой гипотезой: 

;

;

;

;

;

;

;

.

                                       

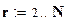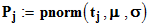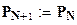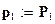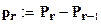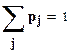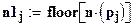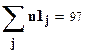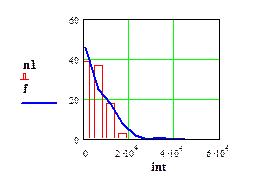
Рис 11. Гистограмма частот отказов при нормальном законе распределения и  полигон частот исходной выборки

 

 

                      

 

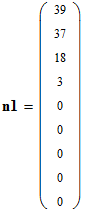
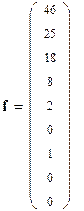
Вычисление критерия Хи-квадрат Пирсона при гипотезе нормального закона распределения наработок до отказа:

;

.

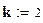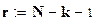Число степеней свободы

.

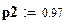Доверительная вероятность

;

.

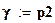 Квантиль Хи -квадрат распределения при вероятности 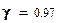и числе степеней свободы  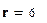равна: .

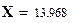Расчётное значение критерия:

;

;

.

 

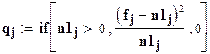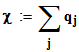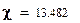 Вывод. Сравнение вычисленного значения критерия 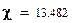 и значения квантили 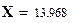показывает, что вычисленное значение меньше. Это позволяет сделать вывод о том, что гипотеза распределения отказов в анализируемой выборке наработок до отказа по нормальному закону может быть принята   с уровнем доверия .

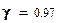Примечание. Для получения согласия при проверке гипотезы может потребоваться корректировка математического ожидания, полученного по статистической выборке.

 

Гипотеза №3. Распределение исходных данных о наработке до отказа соответствует закону Вейбулла

 

Параметры закона Вейбулла:

;

;

;

;

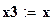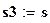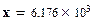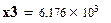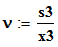-коэффициент вариации;

;

.

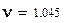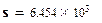Параметр формы в распределении Вейбулла находятся по одной их формул: при коэффициенте вариации меньше единицы первая формула, а в противном случае - вторая.

;

;

;

;

;

;

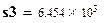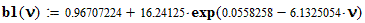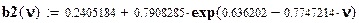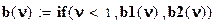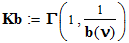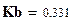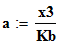-параметр масштаба в распределении Вейбулла;

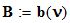-параметр формы в распределении Вейбулла.

Вероятность попадания случайной величины в заданный интервал при распределении Вейбулла находится по формуле:

;

;

;

;

;

.

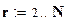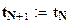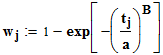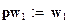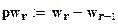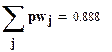Число отказов в выделенных интервалах наработки объекта при законе Вейбулла равно:

;

.

 

                               

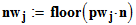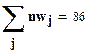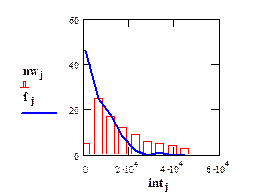
Рис.12. Гистограмма при распределении наработок до отказа по закону Вейбулла и полигон частот исходной выборки

Вычисление критерия Хи-квадрат Пирсона при законе распределения наработок до отказа соответствующего распределению Вейбулла :

;

;

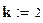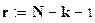Число степеней свободы .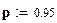

Доверительная вероятность

;

.

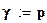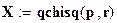 Квантиль Хи -квадрат распределения при вероятности 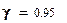 и числе степеней свободы  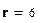 равна: .

                                                                                         

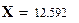Расчётное значение критерия:

;

.

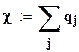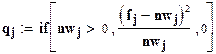 Вывод. Сравнение вычисленного значения критерия 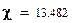 и значения квантили 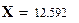показывает, что вычисленное значение больше. Это позволяет сделать вывод о том, что распределение отказов в анализируемой выборке наработок до отказа  не соответствует закону Вейбулла. Вывод сделан с уровнем доверия 0,95.

 

Лабораторная работа №3