СИСТЕМ”
Методические указания к комплексу лабораторных работ
и контрольные задания для студентов
специальностей 220301 “Автоматизация технологических процессов и
производств” (в машиностроении), 280101 “Безопасность жизнедеятельности в техносфере”, направлений подготовки 220400.62 «Управление в технических системах», 220700.62 «Автоматизация технологических процессов и
производств», 280700.62»Техносферная безопасность»
Курган 2012
Кафедра автоматизации производственных процессов
Дисциплина “Надежность технических систем”, “Диагностика и надежность автоматизированных систем” (специальности 220301, 280101, 140211)
Cоставили: канд.техн.наук, доц. Кузнецов В.П.
ст.преп. Дмитриева О.В.
Утверждены на заседании кафедры “ 2 ” сентября 2004г.
Рекомендованы методическим советом университета
“____”_________2004г.
СОДЕРЖАНИЕ
| Введение | 4 |
| 1. Теоретическое введение 1.1. Основные проблемы надежности технических объектов 1.2. Показатели надежности невосстанавливаемых объектов 1.3. Показатели надежности объектов, восстанавливаемых в процессе применения 1.4. Интервальные оценки | 5 5 6 6 8 |
| 2. Различные виды распределения 2.1. Равномерное распределение на отрезке 2.2. Показательное распределение 2.3. Нормальное распределение 2.4. Гамма-распределение 2.5. ХИ-квадрат распределение 2.6. Распределение Вейбулла 2.7. Квантиль функции распределения | 8 9 9 10 11 12 12 13 |
| 3. О выборе теоретического распределения наработки до отказа | 14 |
| 4. Проверка согласия эмпирического закона распределения случайной величины и выдвинутой гипотезы | 14 |
| 5. Цепи Маркова без поглощения | 15 |
| 6. Цепи Маркова с поглощением | 16 |
| 7. Задания для выполнения работ 7.1. Лабораторная работа №1 7.2. Лабораторная работа №2 7.3. Лабораторная работа №3 7.4. Лабораторная работа №4 7.5. Лабораторная работа №5 | 17 17 18 20 21 23 |
| Приложения | 25 |
| Литература | 42 |
Введение
Программы расчёта надёжности технических объектов выполнены в среде MATHCAD 2000, которая исключительно удобна для решения учебных задач. Каждая решаемая задача содержит блок исходной информации, подробный алгоритм вычисления основных показателей и снабжена необходимыми пояснениями и графиками. Заканчивается каждый алгоритм постановкой задачи на самостоятельное исследование, которое должен выполнить обучающийся. Результаты такого исследования отражаются в выводах, составленных по рекомендованной форме, но с результатами, полученными индивидуально каждым обучающимся.
Для всех практических работ подготовлены контрольные вопросы, ответы на которые должен знать исполнитель к моменту защиты. Эти вопросы приведены в конце каждой работы.
Перед началом выполнения практической работы студент должен прослушать лекции по соответствующей теме или проработать материал самостоятельно по рекомендованной литературе.
Цель работы - ознакомиться с различными методами расчета надежности объектов с помощью программы MathCad.
1. Теоретическое введение
1.1. Основные проблемы надежности
технических объектов
Теория надежности изучает процессы возникновения отказов объектов и способы борьбы с отказами. Для удобства решения задач часто различают два вида объектов: элементы и системы.
Система предназначена для самостоятельного выполнения определенной практической задачи. Элемент является составной частью системы. Обычно элемент не предназначается для самостоятельного применения вне связи с другими элементами. В принципе систему можно разбить на любое число элементов, необходимое для исследования (расчета) надежности. Однако деление системы на элементы нельзя считать произвольным. Каждый элемент должен обладать способностью выполнять в системе определенные функции. Иногда ставится условие, чтобы элемент был такой частью системы, которая может быть восстановлена только путем полной замены.
Различают два основных состояния объектов: работоспособное и неработоспособное. Работоспособным называют состояние объекта, при котором значения всех параметров, характеризующих способность выполнять заданные функции, соответствуют требованиям нормативно-технической и (или) конструкторской документации.
Состояние объекта, при котором значение хотя бы одного параметра, характеризующего способность выполнять заданные функции, не соответствуют требованиям нормативно-технической и (или) конструкторской документации, называют неработоспособными.
Отказ – событие, заключающееся в нарушении работоспособного состояния объекта, то есть в переходе в неработоспособное состояние.
Обычно неработоспособным называют такое состояние объекта, при котором его нельзя применять. Однако возможны задачи, в которых неработоспособным считают состояние объекта, при котором он не может продолжать выполнять свое назначение. Возможны и другие признаки неработоспособного состояния объекта (например, запрещается применение объекта по соображениям безопасности). Поэтому при оценке надежности необходимо заранее оговорить, какое состояние объекта считается неработоспособным.
Для объектов разного назначения и устройства применяются различные показатели надежности. Можно выделить четыре группы технических объектов, различающиеся показателями и методами оценки надежности:
1) невосстанавливаемые объекты, применяемые до первого отказа (резистор, конденсатор);
2) восстанавливаемые вне процесса применения объекта (автопилот);
3) восстанавливаемые в процессе применения объекты, для которых недопустимы перерывы в работе (резервированная линия связи);
4) восстанавливаемые в процессе применения объекты, для которых допустимы кратковременные перерывы в работе (робот, станок).
1.2. Показатели надежности
невосстанавливаемых объектов
Для оценки надежности невосстанавливаемых объектов используют вероятностные характеристики случайной величины – наработки Т объекта от начала его эксплуатации до первого отказа. Под наработкой понимают продолжительность или объем работы объекта, измеряемые в часах, циклах или других единицах.
Полной характеристикой любой случайной величины является ее закон распределения, то есть соотношение между возможными значениями случайной величины и соответствующими этим значениям вероятностями. Распределение наработки до отказа может быть описано с помощью различных показателей надежности невосстанавливаемых объектов. К числу таких показателей относятся: функция надежности р(t); плотность распределения наработки на отказ f(t), интенсивность отказов l(t).
Функцией надежности называют функцию, выражающую вероятность того, что Т – случайная наработка до отказа – будет не менее заданной наработки (0, t), отсчитываемый от начала эксплуатации. Наряду с функцией надежности применяют функцию ненадежности, которая характеризует вероятность отказа объекта на интервале (0, t).
Плотность распределения наработки до отказа f(t) является дифференциальной формой закона распределения наработки до отказа. Плотность f(t) является неотрицательной функцией, причем
.
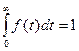График f(t) часто называют кривой распределения наработки до отказа.
1.3. Показатели надежности объектов,
восстанавливаемых в процессе применения
Показатели надежности объектов, восстанавливаемых в процессе применения, вычисляются лишь в календарном времени. Такие объекты можно разделить на две группы.
К первой группе относятся объекты, для которых в течение заданного времени работы допускается отказы и вызванные ими кратковременные перерывы в работе. Для объектов этой группы большое значение имеет свойство готовности – способности находиться в процессе эксплуатации значительную долю времени в работоспособном и готовом состоянии.
Ко второй группе относятся объекты, отказы которых в течение заданного времени недопустимы. Если в этих объектах (системах) имеются избыточные элементы, то при отказах некоторых из них объект остается работоспособным и можно проводить ремонт отказавших элементов во время выполнения задачи.
Один и тот же объект может быть отнесен к разным группам в зависимости от режима его применения.
Надежность первой группы может быть оценена при помощи мгновенных и числовых показателей. Одним из мгновенных показателей является параметр потока восстановлений w0(t). Однако обычно применяют вероятность Г(t1) застать объект работоспособным (готовым к применению) в момент времени t1 либо вероятность П(t1) = 1 – Г(t1) того, что объект в момент времени t1 будет неработоспособным (будет находиться в состоянии вынужденного простоя). Зависимость Г(t) называется функцией готовности.
Как Г(t1), так и П(t1) определяются в предположении, что при t = 0 объект работоспособен, т.е. Г(0) = 1, П(0) = 0.
Объект может находиться в момент времени t в работоспособном состоянии при осуществлении одного из двух несовместных событий: 1) объект в течение времени (0, t) не отказал; 2) объект отказывал и восстанавливался и после последнего восстановления больше не отказывал.
Функция готовности Г(t) равна сумме вероятностей появления указанных событий.
Наряду с функцией готовности применяют коэффициент готовности kГ. Согласно ГОСТ 27.002-83, коэффициент готовности определяется как вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени, кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается. Также коэффициент готовности можно понимать как долю времени, в течение которого объект работоспособен, от общего времени эксплуатации объекта.
Надежность восстанавливаемых объектов второй группы (отказы недопустмы, возможно восстановление некоторых элементов во время выполнения задачи) чаще всего оценивают с помощью условной вероятности безотказной работы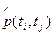 
в течение заданного интервала времени (ti, tj) при условии, что в начальный момент времени все элементы работоспособны.
Отличие 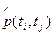от соответствующего показателя для невосстанавливаемого объекта состоит в том, что при вычислении 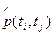учитывается восстановление отказавших элементов при работоспособном объекте (системе). Обычно оценка 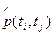для проектируемых объектов производится при допущении о показательных распределениях времени безотказной работы и времени восстановления элементов.
Для объектов второй группы могут в качестве показателей надежности использоваться также параметр потока отказов, средняя наработка на отказ и другие характеристики.
1.4. Интервальные оценки
В оценке показателей надежности вследствие малых объемов наблюдений существуют случайные ошибки. Например, при испытаниях высоконадежных объектов отказы могут не наблюдаться вообще или происходят редко. Значения точечных оценок параметров распределений сильно зависят от количества наблюденных отказов. Поэтому часто целесообразно находить интервальные оценки параметров распределения, определяя границы доверительного интервала, который с доверительной вероятностью g покроет истинное значение параметра распределения при данном объеме выборки.
Интервальной называют оценку, которая определяется двумя числами – концами интервала. Интервальные оценки позволяют установить точность и надежность оценок.
Пусть найденная по данным выборки статистическая характеристика q* служит оценкой неизвестного параметра q. Будем считать q постоянным числом (q может быть и случайной величиной). Ясно, что q* тем точнее определяет параметр q, чем меньше абсолютная величина разности êq – q* ê. Другими словами, если d > 0 и êq – q* ê< d, то, чем меньше d, тем оценка точнее. Таким образом, положительное число d характеризует точность оценки.
Однако статистические методы не позволяют категорически утверждать, что оценка q* удовлетворяет неравенству êq – q* ê< d; можно лишь говорить о вероятности g, с которой это неравенство осуществляется.
Надежностью (доверительной вероятностью) оценки q по q* называют вероятность g, с которой осуществляется неравенство êq – q* ê< d. Обычно надежность оценки задается наперед, причем в качестве g берут число, близкое к единице. Наиболее часто задают надежность, равную 0,95; 0,99 и 0,999.
Пусть вероятность того, что êq – q* ê< d, равна g:
Р[ êq – q* ê< d ] = g.
Заменив неравенство êq – q* ê< d равносильным ему двойным неравенством -d<q - q*<d или q* - d<q<q*+d, имеем
Р[ q* - d<q<q*+d ] = g.
Это соотношение следует понимать так: вероятность того, что интервал (q* - d, q* + d ), заключает в себе (покрывает) неизвестный параметр q, равна g.
Доверительным называют интервал (q* – d, q* +d), который покрывает неизвестный параметр с заданной надежностью g.
2. Различные виды распределения
Возможны два пути оценки показателей надежности невосстанавливаемых объектов по данным об отказах: вычисление экспериментального распределения наработки до отказа и вычисление параметров теоретического распределения наработки до отказа.
Оба пути имеют свои достоинства и недостатки. Исторически сложилось, что вероятностные методы исследования в основном развиваются по пути использования теоретических распределений.
В качестве теоретических распределений наработки до отказа могут быть использованы любые применяемые в теории вероятностей непрерывные распределения. В принципе можно взять любую кривую, площадь под которой равна 1, и использовать ее в качестве кривой распределения случайной величины. Однако существуют различные стандартные виды распределения случайных величин.
2.1. Равномерное распределение в отрезке [c,d]
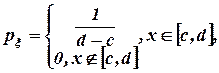
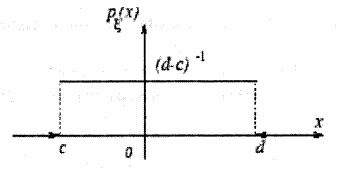
Рис. 1. График равномерного распределения
2.2. Показательное распределение с параметром l >0 
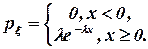
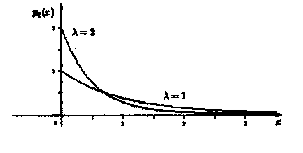
Рис. 2. График показательного распределения
Показательное распределение называют также экспоненциальным. Его применяют чаще других при оценке надежности объектов. Это объясняется рядом причин.
Во-первых, при постоянных интенсивностях отказов получаются очень простые формулы для оценки показателей надежности. Это связано с тем, что при l = const вероятность безотказной работы в течение заданной наработки Dt не зависит от наработки, накопленной до начала интервала Dt.
Во-вторых, показательное распределение наработки до отказа типично для объектов, состоящих из многих элементов с различными распределениями наработки до отказа. Кроме того, для некоторых объектов можно устранить повышенную интенсивность отказов в начальный период эксплуатации применением "тренировки". Если в процессе эксплуатации этих объектов нет периода значительного износа, то интенсивность отказов можно приближенно считать постоянной.
В-третьих, при ограниченных экспериментальных данных трудно обнаружить значительные отклонения от гипотезы l = const, даже если имеется возможная нестационарность l(t). Если экспериментальных данных недостаточно, чтобы выявить истинный характер зависимости l(t), принимают в качестве первого приближения l = const.
2.3. Нормальное распределение
Нормальное (или гауссовское) распределение sÎN(a,s2), a Î R, s > 0:
.
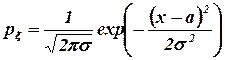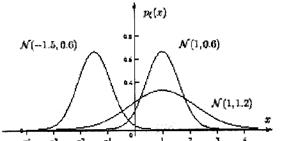
Рис. 3. График нормального распределения
Стандартное нормальное распределение – N(0,1):
.
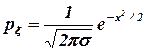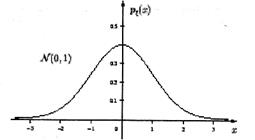
Рис. 4. График стандартного нормального распределения
Необходимо отметить, что вопреки распространенному мнению при отказах элементов за счет износа распределение наработки до отказа будет далеко не всегда нормальным. Часто условием нормального распределения наработки до отказа является малый разброс значений скорости изнашивания элементов. Ввиду большого теоретического и прикладного значения нормального распределения его стараются иногда применить и при явно несимметричных распределениях наработки до отказа. Для этого подбирают некоторую функцию случайной наработки до отказа, например, Y = lg T; Y= T2, с таким расчетом, чтобы случайная величина Y имела приближенно нормальное распределение. Например, довольно часто используется логарифмически нормальное распределение усталостной долговечности, при котором предполагается, что логарифм числа циклов нагрузки до разрушения образца распределен по нормальному закону.
2.4. Гамма-распределение
Плотность гамма-распределения
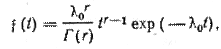
где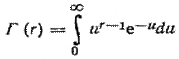 
- гамма-функция.
В теории надежности гамма-распределение обычно используется при целом r. При r = 1 получается показательное распределение. В данном случае показательное распределение – это распределение наработки до первого отказа. При целом r>1 гамма-распределение является распределением суммы r независимых случайных величин, каждая из которых имеет показательное распределение с параметром l0 = 1/mt. Гамма-распределение при целом r иногда называют распределением Эрланга. Для такого распределения
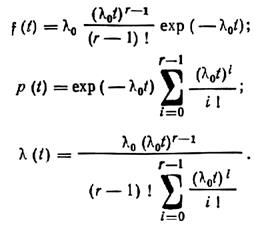
Математическое ожидание наработки до отказа mt = r / l0, дисперсия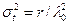 
.
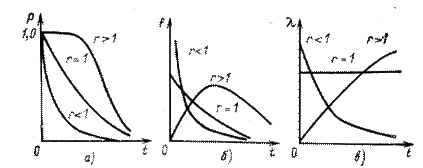
Рис. 5. Графики гамма-распределения:
а - функция надежности; б - кривые распределения; в - интенсивности отказов.
При больших r гамма-распределение сводится нормальному распределению с параметрами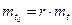 
; 
.
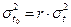В качестве примера использования гамма-распределения представим себе резервированную систему, состоящую из r одинаковых элементов, причем под нагрузкой находится один элемент, а остальные поочередно автоматически включаются в работу после отказа работающего элемента. При показательном распределении наработки до отказа элементов суммарная наработка системы до отказа будет подчинена гамма-распределению.
Хи-квадрат распределение
Пусть x1, …,xn – независимые стандартные нормальные случайные величины (N(0,1)). c2-распределением с n степенями свободы называется распределение следующей случайной величины:
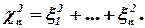
Это распределение сосредоточенно на положительной полуоси и имеет плотность
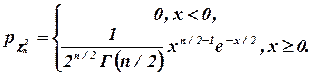
где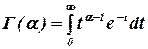 
- гамма-функция.
2.6. Распределение Вейбулла
Плотность распределения Вейбулла
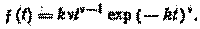
Распределение Вейбулла имеет два параметра: k и n. Параметр k определяет масштаб, при его изменении кривая распределения сжимается или растягивается.
При n = 1 распределение Вейбулла превращается в показательное. Обычно значения n выбирают в пределах от 1 до 2.
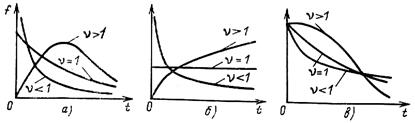
Рис. 6. Графики распределения Вейбулла при k=1:
а – кривые распределения, б – интенсивности отказов,
в – функция надежности
Для распределения Вейбулла функция надежности p(t) и интенсивность отказов l(t) выражаются формулами:
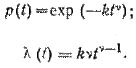
Математическое ожидание наработки до отказа
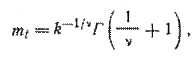
где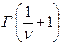 
- гамма-функция.
Распределение Вейбулла иногда используется для описания надежности шариковых подшипников и некоторых типов электронных ламп (n = 1,4¸1,7).
Более подробные сведения об упомянутых выше теоретических распределениях можно найти в соответствующих курсах теории вероятностей.
2.7. Квантиль функции распределения
Будем предполагать, что функция распределения F(t) некоторой непрерывной случайной величины x есть строго возрастающая функция. В дальнейшем a - число между 0 и 1.
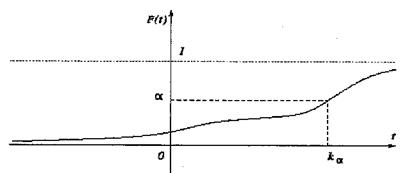
Рис. 7. Функция распределения непрерывной случайной величины
Квантилью уровня a для распределения, порождаемого функцией F(t), называется число ka, являющееся решением уравнения
F(ka) = a.Другими словами, ka = F–1(a), где F–1 : (0,1) à R – функция, обратная к функции F.
Из определения вытекает, что
P{ka1 £ x £ ka2} = a2 – a1,
где 0 < a1 < a2 < 1. В частности, ka монотонно растет по a.
Квантили часто называют также процентными точками распределения.
3. О выборе типа теоретического распределения
наработки до отказа
В настоящее время нет ясного физического толкования происхождения применяемых распределений наработки до отказа.
Вместе с тем, во многих случаях за время эксплуатации или испытаний на надежность успевает отказать лишь незначительная доля первоначально имевшихся объектов. Полученным статистическим данным соответствует начальная (левая) часть экспериментального распределения. Поэтому значения числовых характеристик, найденные в результате обработки опытных данных, сильно зависят от типа предполагаемого распределения наработки до отказа. Например, значения средней наработки до отказа могут различаться в сотни раз.
Для выбора типа теоретического распределения наработки до отказа целесообразно использовать информацию об изменениях в объектах перед возникновением отказов. Для этого необходимо знать, в результате каких физических процессов появляется соответствующее распределение. Иначе говоря, выбранному теоретическому распределению наработки до отказа должна соответствовать определенная модель приближения объекта к отказу. Желательно, чтобы эти модели отражали основные особенности физических процессов приближения к отказам.
Такую оговорку приходится делать потому, что в последние годы при рассмотрении математических вопросов надежности используют модели, которые условно можно назвать формально-вероятностными. Например, может вводиться предположение о вероятности отказа отдельных частей объектов, а не об изменении фактических параметров. Существуют и другие вероятностные модели развития отказов. Эти модели несколько облегчают выбор типа теоретического распределения наработки до отказа. Для осуществления такого выбора необходимы сведения о физических процессах приближения к отказам.
4. Проверка согласия эмпирического закона
распределения случайной величины и выдвинутой гипотезы
Процедура проверки согласия опытного и теоретического распределений случайной величины х заключается в получении упорядоченного ряда результатов наблюдений этой величины
х1 £ х2 £, … , £ хn,
построении на основании их функции накопленных частот и сравнения этой функции с заданной теоретической функцией.
Процедура осуществляется с целью установления функции распределения случайной величины х, применяемой для различных теоретико-вероятностных расчетов, статистического анализа, а также обоснования выборов планов статистического контроля, регулирования и испытаний качества продукции.
Наблюдения случайной величины х должны проводиться в практически одинаковых условиях, исследуемая совокупность должна быть однородной. Нарушение требований однородности может привести к ошибочным выводам.
Число наблюдений случайной величины х для проверки согласия опытного и теоретического распределения должно быть больше 100, если используют критерий Колмогорова и c2, и больше 50, если используют критерий w2.
Для наблюдений случайной величины х должны применяться средства измерения с ценой деления, не превышающей 0,2 предполагаемой величины среднего квадратического отклонения исследуемого распределения.
5. цепи Маркова без поглощения
Формирование моделей для расчета надежности систем и энергоустановок производится с учетом реальных потоков событий, в результате которых происходит эволюция рассматриваемых объектов из состояния в состояние. Потоки событий возникают по причинам отказов, восстановлений, замены, плановых ремонтов элементов систем. Эволюция состояний описывается в виде траекторий переходов из одного состояния в другое с помощью цепей Маркова.
Цепи Маркова отображают возможные состояния системы. При этом каждое состояние рассматривается как результат воздействия возможных событий. Переход из одного состояния в другое осуществляется по дуге, характеризующей интенсивность перехода: частоту отказов или восстановлений (рис. 9).
а)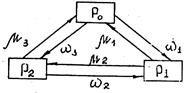 
б)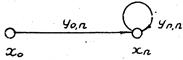 
Рис. 8. Графы цепей Маркова:
а – без поглощения; б – с поглощением
Статистическая модель системы (граф ЦМ), соответствующая графу цепи Маркова, описывается линейными уравнениями вида:
,
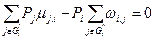где Рi, Рj – вероятности состояний;
mj,I, wI,j – интенсивность переходов;
G'I – подмножество состояний марковского процесса, из которых возможны переходы в i–е состояние;
G"I – подмножество состояний, в которые возможны переходы из i-го состояния.
Для решения системы уравнения (3.1) относительно Рi и Рj дополнительно вводится уравнение нормировки:
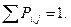
Граф ЦМ, показанный на рисунке 8 а, описывается уравнениями:
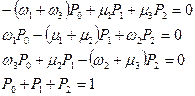
Входящие в эту систему уравнения интенсивности переходов рассчитываются по выражениям:
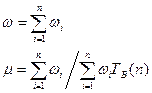
где n – количество элементов в системе или энергоустановке;
Тв(п) – продолжительность восстановительных ремонтов или простоя.
6. Цепи Маркова с поглощением
Граф ЦМ с поглощением описывает процесс последовательного прямого перехода из начального состояния х0 в конечное хn (возможны промежуточные состояния). Конечное состояние в данном случае называется поглощающим, промежуточное – транзитным (рис. 8,б).
При стационарном процессе, когда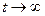 
, элементный граф ЦМ может быть представлен системой уравнений:
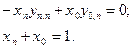
Решение этих уравнений относительно конечного состояния производится подстановкой
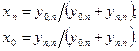
Полученные выражения можно идентифицировать с состояниями элемента (технического или эргатического – человека) до и после отказа с интенсивностью отказа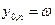 
. Начальное состояние при этом характеризуется коэффициентом готовности х0=kГ (работоспособности), конечное – коэффициентом простоя хп=kп (неработоспособности). Собственный контур конечного состояния определяется интенсивностью восстановлений 
.
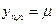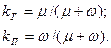
Для эргатического элемента, соответственно: x - интенсивность отказов (1/ч); n - интенсивность восстановлений.
Безотказность – свойство объекта сохранять непрерывно заданные показатели в установленных нормативно-технической документации пределах.
7. Задания для выполнения работ
7.1. Лабораторная работа №1
Таблица 1
| Номер варианта | Количество наблюдаемых объектов, ед. | Количество зафиксированных отказов, ед. | Доверительная вероятность, % |
| 1 | 25 | 7 | 95 |
| 2 | 31 | 2 | 95 |
| 3 | 13 | 3 | 85 |
| 4 | 18 | 1 | 90 |
| 5 | 24 | 3 | 95 |
| 6 | 27 | 4 | 95 |
| 7 | 29 | 2 | 85 |
| 8 | 17 | 5 | 90 |
| 9 | 21 | 8 | 95 |
| 10 | 31 | 9 | 90 |
| 11 | 13 | 6 | 95 |
| 12 | 18 | 7 | 95 |
| 13 | 24 | 2 | 95 |
| 14 | 27 | 3 | 85 |
| 15 | 29 | 5 | 90 |
| 16 | 17 | 4 | 95 |
| 17 | 13 | 3 | 85 |
| 18 | 19 | 5 | 90 |
3. Рассмотреть при различной доверительной вероятности частный случай, когда число отказов L =0.
Результаты исследования отразить в выводах.
1. Вероятность безотказной работы анализируемых объектов находится в интервале от ... до .... Этот результат получен с доверительной вероятностью g =....
2. Для повышения информативности оценки вероятности безотказной работы необходимо увеличить объём выборки исходных данных или определять закон распределения наработок до отказа, что требует новых исходных данных в виде наработок объектов до отказа.
3. С увеличением доверительной вероятности ......
4. С изменением числа отказов от ... до ... интервальные оценки изменяются следующим образом ...
5. При числе отказов, равном нулю ...
Вопросы для защиты лабораторной работы
1. Что такое гарантированная оценка показателей надёжности?
2. Что является пределом верхней интервальной оценки Рбр при доверительной вероятности, стремящейся к единице?
3. Что является пределом нижней интервальной оценки Рбр при доверительной вероятности, стремящейся к единице?
4. Как будет выглядеть гарантированная оценка Рбр при числе отказов равном нулю?
5. Что такое доверительная вероятность?
6. Что такое квантиль функции распределения случайной величины?
7.2. Лабораторная работа №2
Определение закона распределения надёжности невосстанавливаемых
технических объектов по полностью определённой выборке
Исследовать:
1. Определить закон распределения надежности предложенного объекта.
2. Проверить выдвинутую гипотезу.
РЕЗУЛЬТАТ ИССЛЕДОВАНИЙ ОТРАЗИТЬ В ВЫВОДАХ
1. Распределение наработок до отказа для группы анализируемых объектов может быть представлено экспоненциальным законом с параметром l = … или усечённо-нормальным законом с соответствующими параметрами при доверительной вероятности = 0,95.
Таблица 2
| В | Параметр | Номер интервала наблюдения | ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| 1 | Наработка до отказа, ч | 176 | 272 | 368 | 464 | 560 | 656 | 752 | 848 | 944 |
| Количество отказов | 4 | 5 | 12 | 17 | 23 | 24 | 11 | 4 | 0 | |
| 2 | Наработка до отказа, ч | 142 | 268 | 394 | 520 | 646 | 772 | 898 | 1024 | 1150 |
| Количество отказов | 3 | 2 | 14 | 22 | 30 | 15 | 9 | 5 | 0 | |
| 3 | Наработка до отказа, ч | 126 | 4074 | 8022 | 11970 | 15920 | 19870 | 23810 | 27760 | 31710 |
| Количество отказов | 44 | 34 | 9 | 9 | 1 | 0 | 3 | 0 | 0 | |
| 4 | Наработка до отказа, ч | 444 | 570 | 696 | 822 | 948 | 1074 | 1200 | 1326 | 1452 |
| Количество отказов | 3 | 9 | 20 | 20 | 23 | 19 | 6 | 0 | 0 | |
| 5 | Наработка до отказа, ч | 139 | 283 | 427 | 571 | 715 | 859 | 1003 | 1147 | 1291 |
| Количество отказов | 2 | 1 | 10 | 25 | 31 | 19 | 9 | 3 | 0 | |
| 6 | Наработка до отказа, ч | 16 | 3742 | 7468 | 11190 | 14920 | 18650 | 22370 | 26100 | 29820 |
| Количество отказов | 58 | 25 | 7 | 7 | 3 | 0 | 0 | 0 | 0 | |
| 7 | Наработка до отказа, ч | 312 | 510 | 708 | 906 | 1104 | 1302 | 1500 | 1698 | 1896 |
| Количество отказов | 4 | 7 | 18 | 25 | 20 | 19 | 7 | 0 | 0 | |
| 8 | Наработка до отказа, ч | 562 | 709 | 856 | 1003 | 1150 | 1297 | 1444 | 1591 | 1738 |
| Количество отказов | 10 | 5 | 18 | 11 | 23 | 10 | 12 | 11 | 0 | |
| 9 | Наработка до отказа, ч | 674 | 854 | 1034 | 1214 | 1394 | 1574 | 1754 | 1934 | 2114 |
| Количество отказов | 4 | 5 | 22 | 25 | 19 | 13 | 7 | 5 | 0 | |
| 10 | Наработка до отказа, ч | 432 | 686 | 940 | 1194 | 1448 | 1702 | 1956 | 2210 | 2464 |
| Количество отказов | 5 | 2 | 14 | 31 | 27 | 14 | 7 | 0 | 0 | |
| 11 | Наработка до отказа, ч | 482 | 714 | 946 | 1178 | 1410 | 1642 | 1874 | 2106 | 2338 |
| Количество отказов | 4 | 7 | 10 | 23 | 25 | 20 | 8 | 3 | 0 | |
| 12 | Наработка до отказа, ч | 489 | 791 | 1093 | 1395 | 1697 | 1999 | 2301 | 2603 | 2905 |
| Количество отказов | 3 | 4 | 23 | 34 | 23 | 9 | 3 | 1 | 0 | |
2. По внешнему виду гистограммы распределения и полигона частот при проверке третьей гипотезы можно сделать вывод, что соответствующей корректурой параметров формы и масштаба можно подтвердить согласие и с законом Вейбулла.
3. Возможными причинами отказов могут быть:
- нарушение уровня функционирования из-за постепенного изменения параметров объекта;
- исчерпание запасов прочности узлов, ресурс которых определяется износом;
- исчерпание долговечности узлов, элементов и деталей, которым предусмотрен плановый капитальный ремонт;
- наработка до предельного состояния невосстанавливаемых элементов;
- отказ элементов из-за механического разрушения деталей вследствие накопления усталостных повреждений.
Вопросы для защиты ЛАБОРАТОРНОЙ работы
1. Как проверяется согласие эмпирического закона распределения случайной величины и выдвинутой гипотезы?
2. Что такое квантиль функции распределения случайной величины?
3. В каких случаях на практике встречается экспоненциальный закон распределения наработок до отказа?
4. Какие отказы чаще всего приводят к распределению наработок по закону Вейбулла?
5. Как по внешнему виду гистограммы можно обоснованно выдвинуть гипотезу о законе распределения случайной величины?
7.3. Лабораторная работа №3
Вариант
Среднее время безотказной
Работы, ч
Вариант
Лабораторная работа №1
Лабораторная работа №3
Лабораторная работа №4
Лабораторная работа № 5
СИСТЕМ”
для студентов
специальностей 220301 “Автоматизация технологических процессов и
производств” (в машиностроении), 280101 “Безопасность жизнедеятельности в техносфере”, 140211 “Электроснабжение”
Редактор Т.В.Тимофеева
__________________________________________________________________
Подписано к печати Бумага тип.№1
Формат 60х84 1/16 Усл.печ.л. Уч.изд.л.
Заказ Тираж 150 Цена свободная
Издательство Курганского государственного университета.
640669, г.Курган, ул.Гоголя 25.
Курганский государственный университет, ризограф.
СИСТЕМ”
Методические указания к комплексу лабораторных работ
и контрольные задания для студентов
специальностей 220301 “Автоматизация технологических процессов и
производств” (в машиностроении), 280101 “Безопасность жизнедеятельности в техносфере”, направлений подготовки 220400.62 «Управление в технических системах», 220700.62 «Автоматизация технологических процессов и
производств», 280700.62»Техносферная безопасность»
Курган 2012
Кафедра автоматизации производственных процессов
Дисциплина “Надежность технических систем”, “Диагностика и надежность автоматизированных систем” (специальности 220301, 280101, 140211)
Cоставили: канд.техн.наук, доц. Кузнецов В.П.
ст.преп. Дмитриева О.В.
Утверждены на заседании кафедры “ 2 ” сентября 2004г.
Рекомендованы методическим советом университета
“____”_________2004г.
СОДЕРЖАНИЕ
| Введение | 4 |
| 1. Теоретическое введение 1.1. Основные проблемы надежности технических объектов 1.2. Показатели надежности невосстанавливаемых объектов 1.3. Показатели надежности объектов, восстанавливаемых в процессе применения 1.4. Интервальные оценки | 5 5 6 6 8 |
| 2. Различные виды распределения 2.1. Равномерное распределение на отрезке 2.2. Показательное распределение 2.3. Нормальное распределение 2.4. Гамма-распределение 2.5. ХИ-квадрат распределение 2.6. Распределение Вейбулла 2.7. Квантиль функции распределения | 8 9 9 10 11 12 12 13 |
| 3. О выборе теоретического распределения наработки до отказа | 14 |
| 4. Проверка согласия эмпирического закона распределения случайной величины и выдвинутой гипотезы | 14 |
| 5. Цепи Маркова без поглощения | 15 |
| 6. Цепи Маркова с поглощением | 16 |
| 7. Задания для выполнения работ 7.1. Лабораторная работа №1 7.2. Лабораторная работа №2 7.3. Лабораторная работа №3 7.4. Лабораторная работа №4 7.5. Лабораторная работа №5 | 17 17 18 20 21 23 |
| Приложения | 25 |
| Литература | 42 |
Введение
Программы расчёта надёжности технических объектов выполнены в среде MATHCAD 2000, которая исключительно удобна для решения учебных задач. Каждая решаемая задача содержит блок исходной информации, подробный алгоритм вычисления основных показателей и снабжена необходимыми пояснениями и графиками. Заканчивается каждый алгоритм постановкой задачи на самостоятельное исследование, которое должен выполнить обучающийся. Результаты такого исследования отражаются в выводах, составленных по рекомендованной форме, но с результатами, полученными индивидуально каждым обучающимся.
Для всех практических работ подготовлены контрольные вопросы, ответы на которые должен знать исполнитель к моменту защиты. Эти вопросы приведены в конце каждой работы.
Перед началом выполнения практической работы студент должен прослушать лекции по соответствующей теме или проработать материал самостоятельно по рекомендованной литературе.
Цель работы - ознакомиться с различными методами расчета надежности объектов с помощью программы MathCad.
1. Теоретическое введение
1.1. Основные проблемы надежности
технических объектов
Теория надежности изучает процессы возникновения отказов объектов и способы борьбы с отказами. Для удобства решения задач часто различают два вида объектов: элементы и системы.
Система предназначена для самостоятельного выполнения определенной практической задачи. Элемент является составной частью системы. Обычно элемент не предназначается для самостоятельного применения вне связи с другими элементами. В принципе систему можно разбить на любое число элементов, необходимое для исследования (расчета) надежности. Однако деление системы на элементы нельзя считать произвольным. Каждый элемент должен обладать способностью выполнять в системе определенные функции. Иногда ставится условие, чтобы элемент был такой частью системы, которая может быть восстановлена только путем полной замены.
Различают два основных состояния объектов: работоспособное и неработоспособное. Работоспособным называют состояние объекта, при котором значения всех параметров, характеризующих способность выполнять заданные функции, соответствуют требованиям нормативно-технической и (или) конструкторской документации.
Состояние объекта, при котором значение хотя бы одного параметра, характеризующего способность выполнять заданные функции, не соответствуют требованиям нормативно-технической и (или) конструкторской документации, называют неработоспособными.
Отказ – событие, заключающееся в нарушении работоспособного состояния объекта, то есть в переходе в неработоспособное состояние.
Обычно неработоспособным называют такое состояние объекта, при котором его нельзя применять. Однако возможны задачи, в которых неработоспособным считают состояние объекта, при котором он не может продолжать выполнять свое назначение. Возможны и другие признаки неработоспособного состояния объекта (например, запрещается применение объекта по соображениям безопасности). Поэтому при оценке надежности необходимо заранее оговорить, какое состояние объекта считается неработоспособным.
Для объектов разного назначения и устройства применяются различные показатели надежности. Можно выделить четыре группы технических объектов, различающиеся показателями и методами оценки надежности:
1) невосстанавливаемые объекты, применяемые до первого отказа (резистор, конденсатор);
2) восстанавливаемые вне процесса применения объекта (автопилот);
3) восстанавливаемые в процессе применения объекты, для которых недопустимы перерывы в работе (резервированная линия связи);
4) восстанавливаемые в процессе применения объекты, для которых допустимы кратковременные перерывы в работе (робот, станок).
1.2. Показатели надежности
невосстанавливаемых объектов
Для оценки надежности невосстанавливаемых объектов используют вероятностные характеристики случайной величины – наработки Т объекта от начала его эксплуатации до первого отказа. Под наработкой понимают продолжительность или объем работы объекта, измеряемые в часах, циклах или других единицах.
Полной характеристикой любой случайной величины является ее закон распределения, то есть соотношение между возможными значениями случайной величины и соответствующими этим значениям вероятностями. Распределение наработки до отказа может быть описано с помощью различных показателей надежности невосстанавливаемых объектов. К числу таких показателей относятся: функция надежности р(t); плотность распределения наработки на отказ f(t), интенсивность отказов l(t).
Функцией надежности называют функцию, выражающую вероятность того, что Т – случайная наработка до отказа – будет не менее заданной наработки (0, t), отсчитываемый от начала эксплуатации. Наряду с функцией надежности применяют функцию ненадежности, которая характеризует вероятность отказа объекта на интервале (0, t).
Плотность распределения наработки до отказа f(t) является дифференциальной формой закона распределения наработки до отказа. Плотность f(t) является неотрицательной функцией, причем
.
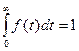График f(t) часто называют кривой распределения наработки до отказа.
1.3. Показатели надежности объектов,
восстанавливаемых в процессе применения
Показатели надежности объектов, восстанавливаемых в процессе применения, вычисляются лишь в календарном времени. Такие объекты можно разделить на две группы.
К первой группе относятся объекты, для которых в течение заданного времени работы допускается отказы и вызванные ими кратковременные перерывы в работе. Для объектов этой группы большое значение имеет свойство готовности – способности находиться в процессе эксплуатации значительную долю времени в работоспособном и готовом состоянии.
Ко второй группе относятся объекты, отказы которых в течение заданного времени недопустимы. Если в этих объектах (системах) имеются избыточные элементы, то при отказах некоторых из них объект остается работоспособным и можно проводить ремонт отказавших элементов во время выполнения задачи.
Один и тот же объект может быть отнесен к разным группам в зависимости от режима его применения.
Надежность первой группы может быть оценена при помощи мгновенных и числовых показателей. Одним из мгновенных показателей является параметр потока восстановлений w0(t). Однако обычно применяют вероятность Г(t1) застать объект работоспособным (готовым к применению) в момент времени t1 либо вероятность П(t1) = 1 – Г(t1) того, что объект в момент времени t1 будет неработоспособным (будет находиться в состоянии вынужденного простоя). Зависимость Г(t) называется функцией готовности.
Как Г(t1), так и П(t1) определяются в предположении, что при t = 0 объект работоспособен, т.е. Г(0) = 1, П(0) = 0.
Объект может находиться в момент времени t в работоспособном состоянии при осуществлении одного из двух несовместных событий: 1) объект в течение времени (0, t) не отказал; 2) объект отказывал и восстанавливался и после последнего восстановления больше не отказывал.
Функция готовности Г(t) равна сумме вероятностей появления указанных событий.
Наряду с функцией готовности применяют коэффициент готовности kГ. Согласно ГОСТ 27.002-83, коэффициент готовности определяется как вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени, кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается. Также коэффициент готовности можно понимать как долю времени, в течение которого объект работоспособен, от общего времени эксплуатации объекта.
Надежность восстанавливаемых объектов второй группы (отказы недопустмы, возможно восстановление некоторых элементов во время выполнения задачи) чаще всего оценивают с помощью условной вероятности безотказной работы 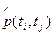в течение заданного интервала времени (ti, tj) при условии, что в начальный момент времени все элементы работоспособны.
Отличие 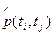от соответствующего показателя для невосстанавливаемого объекта состоит в том, что при вычислении 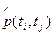учитывается восстановление отказавших элементов при работоспособном объекте (системе). Обычно оценка 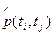для проектируемых объектов производится при допущении о показательных распределениях времени безотказной работы и времени восстановления элементов.
Для объектов второй группы могут в качестве показателей надежности использоваться также параметр потока отказов, средняя наработка на отказ и другие характеристики.
1.4. Интервальные оценки
В оценке показателей надежности вследствие малых объемов наблюдений существуют случайные ошибки. Например, при испытаниях высоконадежных объектов отказы могут не наблюдаться вообще или происходят редко. Значения точечных оценок параметров распределений сильно зависят от количества наблюденных отказов. Поэтому часто целесообразно находить интервальные оценки параметров распределения, определяя границы доверительного интервала, который с доверительной вероятностью g покроет истинное значение параметра распределения при данном объеме выборки.
Интервальной называют оценку, которая определяется двумя числами – концами интервала. Интервальные оценки позволяют установить точность и надежность оценок.
Пусть найденная по данным выборки статистическая характеристика q* служит оценкой неизвестного параметра q. Будем считать q постоянным числом (q может быть и случайной величиной). Ясно, что q* тем точнее определяет параметр q, чем меньше абсолютная величина разности êq – q* ê. Другими словами, если d > 0 и êq – q* ê< d, то, чем меньше d, тем оценка точнее. Таким образом, положительное число d характеризует точность оценки.
Однако статистические методы не позволяют категорически утверждать, что оценка q* удовлетворяет неравенству êq – q* ê< d; можно лишь говорить о вероятности g, с которой это неравенство осуществляется.
Надежностью (доверительной вероятностью) оценки q по q* называют вероятность g, с которой осуществляется неравенство êq – q* ê< d. Обычно надежность оценки задается наперед, причем в качестве g берут число, близкое к единице. Наиболее часто задают надежность, равную 0,95; 0,99 и 0,999.
Пусть вероятность того, что êq – q* ê< d, равна g:
Р[ êq – q* ê< d ] = g.
Заменив неравенство êq – q* ê< d равносильным ему двойным неравенством -d<q - q*<d или q* - d<q<q*+d, имеем
Р[ q* - d<q<q*+d ] = g.
Это соотношение следует понимать так: вероятность того, что интервал (q* - d, q* + d ), заключает в себе (покрывает) неизвестный параметр q, равна g.
Доверительным называют интервал (q* – d, q* +d), который покрывает неизвестный параметр с заданной надежностью g.
2. Различные виды распределения
Возможны два пути оценки показателей надежности невосстанавливаемых объектов по данным об отказах: вычисление экспериментального распределения наработки до отказа и вычисление параметров теоретического распределения наработки до отказа.
Оба пути имеют свои достоинства и недостатки. Исторически сложилось, что вероятностные методы исследования в основном развиваются по пути использования теоретических распределений.
В качестве теоретических распределений наработки до отказа могут быть использованы любые применяемые в теории вероятностей непрерывные распределения. В принципе можно взять любую кривую, площадь под которой равна 1, и использовать ее в качестве кривой распределения случайной величины. Однако существуют различные стандартные виды распределения случайных величин.
2.1. Равномерное распределение в отрезке [c,d]
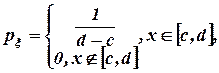
Рис. 1. График равномерного распределения
2.2. Показательное распределение с параметром l >0
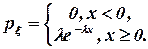
Рис. 2. График показательного распределения
Показательное распределение называют также экспоненциальным. Его применяют чаще других при оценке надежности объектов. Это объясняется рядом причин.
Во-первых, при постоянных интенсивностях отказов получаются очень простые формулы для оценки показателей надежности. Это связано с тем, что при l = const вероятность безотказной работы в течение заданной наработки Dt не зависит от наработки, накопленной до начала интервала Dt.
Во-вторых, показательное распределение наработки до отказа типично для объектов, состоящих из многих элементов с различными распределениями наработки до отказа. Кроме того, для некоторых объектов можно устранить повышенную интенсивность отказов в начальный период эксплуатации применением "тренировки". Если в процессе эксплуатации этих объектов нет периода значительного износа, то интенсивность отказов можно приближенно считать постоянной.
В-третьих, при ограниченных экспериментальных данных трудно обнаружить значительные отклонения от гипотезы l = const, даже если имеется возможная нестационарность l(t). Если экспериментальных данных недостаточно, чтобы выявить истинный характер зависимости l(t), принимают в качестве первого приближения l = const.
2.3. Нормальное распределение
Нормальное (или гауссовское) распределение sÎN(a,s2), a Î R, s > 0:
.
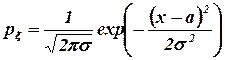Рис. 3. График нормального распределения
Стандартное нормальное распределение – N(0,1):
.
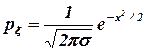Рис. 4. График стандартного нормального распределения
Необходимо отметить, что вопреки распространенному мнению при отказах элементов за счет износа распределение наработки до отказа будет далеко не всегда нормальным. Часто условием нормального распределения наработки до отказа является малый разброс значений скорости изнашивания элементов. Ввиду большого теоретического и прикладного значения нормального распределения его стараются иногда применить и при явно несимметричных распределениях наработки до отказа. Для этого подбирают некоторую функцию случайной наработки до отказа, например, Y = lg T; Y= T2, с таким расчетом, чтобы случайная величина Y имела приближенно нормальное распределение. Например, довольно часто используется логарифмически нормальное распределение усталостной долговечности, при котором предполагается, что логарифм числа циклов нагрузки до разрушения образца распределен по нормальному закону.
2.4. Гамма-распределение
Плотность гамма-распределения
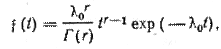
где 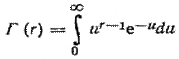- гамма-функция.
В теории надежности гамма-распределение обычно используется при целом r. При r = 1 получается показательное распределение. В данном случае показательное распределение – это распределение наработки до первого отказа. При целом r>1 гамма-распределение является распределением суммы r независимых случайных величин, каждая из которых имеет показательное распределение с параметром l0 = 1/mt. Гамма-распределение при целом r иногда называют распределением Эрланга. Для такого распределения
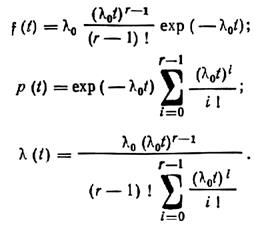
Математическое ожидание наработки до отказа mt = r / l0, дисперсия .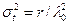
Рис. 5. Графики гамма-распределения:
а - функция надежности; б - кривые распределения; в - интенсивности отказов.
При больших r гамма-распределение сводится нормальному распределению с параметрами ; .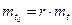
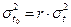В качестве примера использования гамма-распределения представим себе резервированную систему, состоящую из r одинаковых элементов, причем под нагрузкой находится один элемент, а остальные поочередно автоматически включаются в работу после отказа работающего элемента. При показательном распределении наработки до отказа элементов суммарная наработка системы до отказа будет подчинена гамма-распределению.
Хи-квадрат распределение
Пусть x1, …,xn – независимые стандартные нормальные случайные величины (N(0,1)). c2-распределением с n степенями свободы называется распределение следующей случайной величины:
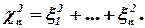
Это распределение сосредоточенно на положительной полуоси и имеет плотность
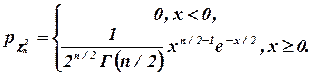
где 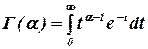- гамма-функция.
2.6. Распределение Вейбулла
Плотность распределения Вейбулла
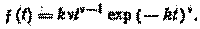
Распределение Вейбулла имеет два параметра: k и n. Параметр k определяет масштаб, при его изменении кривая распределения сжимается или растягивается.
При n = 1 распределение Вейбулла превращается в показательное. Обычно значения n выбирают в пределах от 1 до 2.
Рис. 6. Графики распределения Вейбулла при k=1:
а – кривые распределения, б – интенсивности отказов,
в – функция надежности
Для распределения Вейбулла функция надежности p(t) и интенсивность отказов l(t) выражаются формулами:
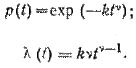
Математическое ожидание наработки до отказа
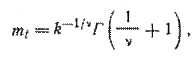
где 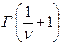- гамма-функция.
Распределение Вейбулла иногда используется для описания надежности шариковых подшипников и некоторых типов электронных ламп (n = 1,4¸1,7).
Более подробные сведения об упомянутых выше теоретических распределениях можно найти в соответствующих курсах теории вероятностей.
2.7. Квантиль функции распределения
Будем предполагать, что функция распределения F(t) некоторой непрерывной случайной величины x есть строго возрастающая функция. В дальнейшем a - число между 0 и 1.
Рис. 7. Функция распределения непрерывной случайной величины
Квантилью уровня a для распределения, порождаемого функцией F(t), называется число ka, являющееся решением уравнения
F(ka) = a.Другими словами, ka = F–1(a), где F–1 : (0,1) à R – функция, обратная к функции F.
Из определения вытекает, что
P{ka1 £ x £ ka2} = a2 – a1,
где 0 < a1 < a2 < 1. В частности, ka монотонно растет по a.
Квантили часто называют также процентными точками распределения.
3. О выборе типа теоретического распределения
наработки до отказа
В настоящее время нет ясного физического толкования происхождения применяемых распределений наработки до отказа.
Вместе с тем, во многих случаях за время эксплуатации или испытаний на надежность успевает отказать лишь незначительная доля первоначально имевшихся объектов. Полученным статистическим данным соответствует начальная (левая) часть экспериментального распределения. Поэтому значения числовых характеристик, найденные в результате обработки опытных данных, сильно зависят от типа предполагаемого распределения наработки до отказа. Например, значения средней наработки до отказа могут различаться в сотни раз.
Для выбора типа теоретического распределения наработки до отказа целесообразно использовать информацию об изменениях в объектах перед возникновением отказов. Для этого необходимо знать, в результате каких физических процессов появляется соответствующее распределение. Иначе говоря, выбранному теоретическому распределению наработки до отказа должна соответствовать определенная модель приближения объекта к отказу. Желательно, чтобы эти модели отражали основные особенности физических процессов приближения к отказам.
Такую оговорку приходится делать потому, что в последние годы при рассмотрении математических вопросов надежности используют модели, которые условно можно назвать формально-вероятностными. Например, может вводиться предположение о вероятности отказа отдельных частей объектов, а не об изменении фактических параметров. Существуют и другие вероятностные модели развития отказов. Эти модели несколько облегчают выбор типа теоретического распределения наработки до отказа. Для осуществления такого выбора необходимы сведения о физических процессах приближения к отказам.
4. Проверка согласия эмпирического закона
распределения случайной величины и выдвинутой гипотезы
Процедура проверки согласия опытного и теоретического распределений случайной величины х заключается в получении упорядоченного ряда результатов наблюдений этой величины
х1 £ х2 £, … , £ хn,
построении на основании их функции накопленных частот и сравнения этой функции с заданной теоретической функцией.
Процедура осуществляется с целью установления функции распределения случайной величины х, применяемой для различных теоретико-вероятностных расчетов, статистического анализа, а также обоснования выборов планов статистического контроля, регулирования и испытаний качества продукции.
Наблюдения случайной величины х должны проводиться в практически одинаковых условиях, исследуемая совокупность должна быть однородной. Нарушение требований однородности может привести к ошибочным выводам.
Число наблюдений случайной величины х для проверки согласия опытного и теоретического распределения должно быть больше 100, если используют критерий Колмогорова и c2, и больше 50, если используют критерий w2.
Для наблюдений случайной величины х должны применяться средства измерения с ценой деления, не превышающей 0,2 предполагаемой величины среднего квадратического отклонения исследуемого распределения.
5. цепи Маркова без поглощения
Формирование моделей для расчета надежности систем и энергоустановок производится с учетом реальных потоков событий, в результате которых происходит эволюция рассматриваемых объектов из состояния в состояние. Потоки событий возникают по причинам отказов, восстановлений, замены, плановых ремонтов элементов систем. Эволюция состояний описывается в виде траекторий переходов из одного состояния в другое с помощью цепей Маркова.
Цепи Маркова отображают возможные состояния системы. При этом каждое состояние рассматривается как результат воздействия возможных событий. Переход из одного состояния в другое осуществляется по дуге, характеризующей интенсивность перехода: частоту отказов или восстановлений (рис. 9).
а)
б)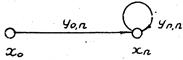
Рис. 8. Графы цепей Маркова:
а – без поглощения; б – с поглощением
Статистическая модель системы (граф ЦМ), соответствующая графу цепи Маркова, описывается линейными уравнениями вида:
,
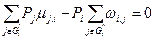где Рi, Рj – вероятности состояний;
mj,I, wI,j – интенсивность переходов;
G'I – подмножество состояний марковского процесса, из которых возможны переходы в i–е состояние;
G"I – подмножество состояний, в которые возможны переходы из i-го состояния.
Для решения системы уравнения (3.1) относительно Рi и Рj дополнительно вводится уравнение нормировки:
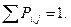
Граф ЦМ, показанный на рисунке 8 а, описывается уравнениями:
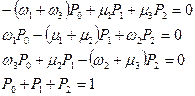
Входящие в эту систему уравнения интенсивности переходов рассчитываются по выражениям:
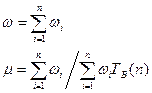
где n – количество элементов в системе или энергоустановке;
Тв(п) – продолжительность восстановительных ремонтов или простоя.
6. Цепи Маркова с поглощением
Граф ЦМ с поглощением описывает процесс последовательного прямого перехода из начального состояния х0 в конечное хn (возможны промежуточные состояния). Конечное состояние в данном случае называется поглощающим, промежуточное – транзитным (рис. 8,б).
При стационарном процессе, когда 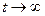, элементный граф ЦМ может быть представлен системой уравнений:
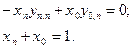
Решение этих уравнений относительно конечного состояния производится подстановкой
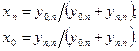
Полученные выражения можно идентифицировать с состояниями элемента (технического или эргатического – человека) до и после отказа с интенсивностью отказа 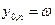. Начальное состояние при этом характеризуется коэффициентом готовности х0=kГ (работоспособности), конечное – коэффициентом простоя хп=kп (неработоспособности). Собственный контур конечного состояния определяется интенсивностью восстановлений .
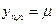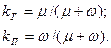
Для эргатического элемента, соответственно: x - интенсивность отказов (1/ч); n - интенсивность восстановлений.
Безотказность – свойство объекта сохранять непрерывно заданные показатели в установленных нормативно-технической документации пределах.
7. Задания для выполнения работ
7.1. Лабораторная работа №1
Интервальная оценка показателей безотказности
Исследовать:
1. Влияние величины доверительной вероятности на интервал гарантированной оценки вероятности безотказной работы.
2. Влияние числа отказов на размер области гарантированной оценки вероятности безотказной работы.
Таблица 1
| Номер варианта | Количество наблюдаемых объектов, ед. | Количество зафиксированных отказов, ед. | Доверительная вероятность, % |
| 1 | 25 | 7 | 95 |
| 2 | 31 | 2 | 95 |
| 3 | 13 | 3 | 85 |
| 4 | 18 | 1 | 90 |
| 5 | 24 | 3 | 95 |
| 6 | 27 | 4 | 95 |
| 7 | 29 | 2 | 85 |
| 8 | 17 | 5 | 90 |
| 9 | 21 | 8 | 95 |
| 10 | 31 | 9 | 90 |
| 11 | 13 | 6 | 95 |
| 12 | 18 | 7 | 95 |
| 13 | 24 | 2 | 95 |
| 14 | 27 | 3 | 85 |
| 15 | 29 | 5 | 90 |
| 16 | 17 | 4 | 95 |
| 17 | 13 | 3 | 85 |
| 18 | 19 | 5 | 90 |
3. Рассмотреть при различной доверительной вероятности частный случай, когда число отказов L =0.
Результаты исследования отразить в выводах.
1. Вероятность безотказной работы анализируемых объектов находится в интервале от ... до .... Этот результат получен с доверительной вероятностью g =....
2. Для повышения информативности оценки вероятности безотказной работы необходимо увеличить объём выборки исходных данных или определять закон распределения наработок до отказа, что требует новых исходных данных в виде наработок объектов до отказа.
3. С увеличением доверительной вероятности ......
4. С изменением числа отказов от ... до ... интервальные оценки изменяются следующим образом ...
5. При числе отказов, равном нулю ...
Вопросы для защиты лабораторной работы
1. Что такое гарантированная оценка показателей надёжности?
2. Что является пределом верхней интервальной оценки Рбр при доверительной вероятности, стремящейся к единице?
3. Что является пределом нижней интервальной оценки Рбр при доверительной вероятности, стремящейся к единице?
4. Как будет выглядеть гарантированная оценка Рбр при числе отказов равном нулю?
5. Что такое доверительная вероятность?
6. Что такое квантиль функции распределения случайной величины?
7.2. Лабораторная работа №2
Определение закона распределения надёжности невосстанавливаемых
технических объектов по полностью определённой выборке
Исследовать:
1. Определить закон распределения надежности предложенного объекта.
2. Проверить выдвинутую гипотезу.
РЕЗУЛЬТАТ ИССЛЕДОВАНИЙ ОТРАЗИТЬ В ВЫВОДАХ
1. Распределение наработок до отказа для группы анализируемых объектов может быть представлено экспоненциальным законом с параметром l = … или усечённо-нормальным законом с соответствующими параметрами при доверительной вероятности = 0,95.
Таблица 2
| В | Параметр | Номер интервала наблюдения | ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||
| 1 | Наработка до отказа, ч | 176 | 272 | 368 | 464 | 560 | 656 | 752 | 848 | 944 |
| Количество отказов | 4 | 5 | 12 | 17 | 23 | 24 | 11 | 4 | 0 | |
| 2 | Наработка до отказа, ч | 142 | 268 | 394 | 520 | 646 | 772 | 898 | 1024 | 1150 |
| Количество отказов | 3 | 2 | 14 | 22 | 30 | 15 | 9 | 5 | 0 | |
| 3 | Наработка до отказа, ч | 126 | 4074 | 8022 | 11970 | 15920 | 19870 | 23810 | 27760 | 31710 |
| Количество отказов | 44 | 34 | 9 | 9 | 1 | 0 | 3 | 0 | 0 | |
| 4 | Наработка до отказа, ч | 444 | 570 | 696 | 822 | 948 | 1074 | 1200 | 1326 | 1452 |
| Количество отказов | 3 | 9 | 20 | 20 | 23 | 19 | 6 | 0 | 0 | |
| 5 | Наработка до отказа, ч | 139 | 283 | 427 | 571 | 715 | 859 | 1003 | 1147 | 1291 |
| Количество отказов | 2 | 1 | 10 | 25 | 31 | 19 | 9 | 3 | 0 | |
| 6 | Наработка до отказа, ч | 16 | 3742 | 7468 | 11190 | 14920 | 18650 | 22370 | 26100 | 29820 |
| Количество отказов | 58 | 25 | 7 | 7 | 3 | 0 | 0 | 0 | 0 | |
| 7 | Наработка до отказа, ч | 312 | 510 | 708 | 906 | 1104 | 1302 | 1500 | 1698 | 1896 |
| Количество отказов | 4 | 7 | 18 | 25 | 20 | 19 | 7 | 0 | 0 | |
| 8 | Наработка до отказа, ч | 562 | 709 | 856 | 1003 | 1150 | 1297 | 1444 | 1591 | 1738 |
| Количество отказов | 10 | 5 | 18 | 11 | 23 | 10 | 12 | 11 | 0 | |
| 9 | Наработка до отказа, ч | 674 | 854 | 1034 | 1214 | 1394 | 1574 | 1754 | 1934 | 2114 |
| Количество отказов | 4 | 5 | 22 | 25 | 19 | 13 | 7 | 5 | 0 | |
| 10 | Наработка до отказа, ч | 432 | 686 | 940 | 1194 | 1448 | 1702 | 1956 | 2210 | 2464 |
| Количество отказов | 5 | 2 | 14 | 31 | 27 | 14 | 7 | 0 | 0 | |
| 11 | Наработка до отказа, ч | 482 | 714 | 946 | 1178 | 1410 | 1642 | 1874 | 2106 | 2338 |
| Количество отказов | 4 | 7 | 10 | 23 | 25 | 20 | 8 | 3 | 0 | |
| 12 | Наработка до отказа, ч | 489 | 791 | 1093 | 1395 | 1697 | 1999 | 2301 | 2603 | 2905 |
| Количество отказов | 3 | 4 | 23 | 34 | 23 | 9 | 3 | 1 | 0 | |
2. По внешнему виду гистограммы распределения и полигона частот при проверке третьей гипотезы можно сделать вывод, что соответствующей корректурой параметров формы и масштаба можно подтвердить согласие и с законом Вейбулла.
3. Возможными причинами отказов могут быть:
- нарушение уровня функционирования из-за постепенного изменения параметров объекта;
- исчерпание запасов прочности узлов, ресурс которых определяется износом;
- исчерпание долговечности узлов, элементов и деталей, которым предусмотрен плановый капитальный ремонт;
- наработка до предельного состояния невосстанавливаемых элементов;
- отказ элементов из-за механического разрушения деталей вследствие накопления усталостных повреждений.
Вопросы для защиты ЛАБОРАТОРНОЙ работы
1. Как проверяется согласие эмпирического закона распределения случайной величины и выдвинутой гипотезы?
2. Что такое квантиль функции распределения случайной величины?
3. В каких случаях на практике встречается экспоненциальный закон распределения наработок до отказа?
4. Какие отказы чаще всего приводят к распределению наработок по закону Вейбулла?
5. Как по внешнему виду гистограммы можно обоснованно выдвинуть гипотезу о законе распределения случайной величины?
7.3. Лабораторная работа №3
Дата: 2019-02-02, просмотров: 465.
