Определение классов элемента фермы

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Классы элемента фермы определяются для каждого из расчетов по формулам (2.1)–(2.5) и заносятся в таблицу сравнения классов (табл. 2), приведенную ниже.

					Таблица 2

	Длина	Положение	Класс	Класс	Максимально
	Загружения	Положение	Класс	Класс	допустимая
Вид расчета	Загружения	вершины л.в.	элемента	нагрузки	допустимая
Вид расчета	Линии	вершины л.в.	элемента	нагрузки	скорость
	Линии	Α	К	К₀	скорость
	Λ	Α	К	К₀	V, км/ч
	Λ				V, км/ч

На прочность

На устойчивость

На выносливость

Определение класса подвижного состава

В задании № 2 необходимо определить класс перспективного подвижного состава грузоподъёмностью 151 т (или габарита Тпр) принимается по приложению и тяжеловесного транспортера, который следует в составе поезда.

Таблица классификации 28-осного транспортера с грузом 400 т, условия пропуска ко-торого определяются в данном задании, приведена в приложении 9. Классы транспортера К₀ определяются по указанной таблице методом линейной интерполяции для тех же значений длин загружения λ и положений вершины линии влияния α, при которых определялись классы элемента. Полученные классы К₀ заносят в таблицу сравнения классов (табл. 2).

Определение условий пропуска нагрузки

Для определение условий пропуска нагрузки по рассчитанному элементу фермы необходимо сравнить классы элемента К с классами нагрузки К₀.

Скорость движения нагрузки по мосту определяется по графику 1 и заносится в таблицу 2. Если значение скорости получается менее 5 км/час, то вносится запись «пропуск невозможен».

В строке «расчет на выносливость» табл. 2 скорость не определяется, т.к. низкий класс элемента по выносливости не является основанием для ограничения скорости. В этом случае выполняется усиление элемента в полном объеме.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Содержание, реконструкция, усиление и ремонт мостов и труб / В.О. Осипов, Ю.Г.Козьмин и др. по редакцией В.О.Осипова и Ю.Г.Козьмина. – М.: Транспорт, 1996. – 471 с.

2. Руководство по определению грузоподъемности металлических пролетных строений железно-дорожных мостов. – М., 2015. – 398 с.

3. Руководство по пропуску подвижного состава по железнодорожным мостам. – М.,

2015. – 496 с.

ПРИЛОЖЕНИЯ

Основные расчетные сопротивления

Приложение 1 [2] Металл Толщина проката, мм R, МПа (тс/см²) I Сварочное железо (в том числе 160 (1,60) заклепки) Литое железо выплавки до 1906 г. 185 (1,85) (в том числе заклепки) Литое железо выплавки после 1906 г. (в том числе заклепки); стали 190 (1,90) марок: Ст3; Ст3 мост.; М16С 16Д (ГОСТ 6713) До 20 195 (1,95) 16Д (ГОСТ 6713) 21-40 185 (1,85) 16Д (ГОСТ 6713) 41-60 175 (1,75) II 15ХСНД (ГОСТ 6713) 8-32 265 (2,65) 15ХСНД (ГОСТ 6713) 33-55 255 (2,55) 10ХСНД (ГОСТ 6713) 8-15 315 (3,15) 10ХСНД (ГОСТ 6713) 16-32 315 (3,15) 10ХСНД (ГОСТ 6713) 33-40 315 (3,15) 15ХСНД (СТО 13657842-1-2009) 8-50 265 (2,65) 10ХСНД (СТО 13657842-1-2009) 8-50 315 (3,15) 14ХГНДЦ (ТУ 14-4-5355-98*) 8-50 265 (2,65) 09Г2С (ГОСТ 19281) фасонный 265 (2,65) 09Г2СД (ГОСТ 19281) фасонный 265 (2,65) III Стальное литье, в том числе и 170 (1,70) неизвестных марок Стали марок: Ст5 в катках и болтах – шарнирах 200 (2,00) Ст2 (для заклепок) 190 (1,90) 09Г2 (для заклепок и болтов) 240 (2,40) 40Х (для высокопрочных болтов) 770 (7,70) 40Х13 (ГОСТ 5632) круглый 1050(10,50) Чугун, в том числе и неизвестных 55 (0,55) марок, на растяжение при изгибе

Приложение 2

Эталонная временная вертикальная эквивалентная нагрузка k _c схемы С1 для треугольных линий влияния (без учета динамического коэффициента)

	Нагружения			Эталонная нагрузка k_c, кН/м пути (тс/м
					пути)
	линии влияния (λ),									1+18/(30+λ)
				Положение вершины линии влияния
	м,
				α=0		α =0,5

	1			49,03(5,000)		49,03(5,000)				1,5806
	1,5			39,15 (3,992)		34,25 (3,493)				1,5714
	2			30,55(3,115)		26,73 (2,726)				1,5625
	3			24,16(2,464)		21,14 (2,156)				1,5455
	4			21,69(2,212)		18,99 (1,936)				1,5294
	5			20,37(2,077)		17,82 (1,817)				1,5143
	6			19,50(1,988)		17,06 (1,740)				1,5000
	7			18,84(1,921)		16,48 (1,681)				1,4865
	8			18,32(1,868)		16,02 (1,634)				1,4737
	9			17,87(1,822)		15,63 (1,594)				1,4615
	10			17,47(1,781)		15,28 (1,558)				1,4500
	12			16,78(1,711)		14,68 (1,497)				1,4286
	14			16,19(1,651)		14,16 (1,444)				1,4091
	16			15,66(1,597)		13,71 (1,398)				1,3913
	18			15,19(1,549)		13,30 (1,356)				1,3750
	20			14,76(1,505)		12,92 (1,317)				1,3600
	25			13,85(1,412)		12,12 (1,236)				1,3273
	30			13,10(1,336)		11,46 (1,169)				1,3000
	35			12,50(1,275)		10,94 (1,116)				1,2769
	40			12,01(1,225)		10,51 (1,072)				1,2571
	45			11,61(1,184)		10,16 (1,036)				1,2400
	50			11,29(1,151)		9,875 (1,007)				1,2250
	60			10,80(1,101)		9,807 (1,000)				1,2000
	70			10,47(1,068)		9,807		(1,000)		1,1800
	80			10,26(1,046)		9,807 (1,000)				1,1636
	90			10,10(1,030)		9,807 (1,000)				1,1500
		100	10,00(1,020)				9,807 (1,000)		1,1385
		110	9,944(1,014)				9,807 (1,000)		1,1286
		120	9,895(1,009)				9,807 (1,000)		1,1200
		130	9,865(1,006)				9,807 (1,000)		1,1125
		140	9,846(1,004)				9,807 (1,000)		1,1059
		150	9,807(1,000)				9,807 (1,000)		1,1000
		160	9,807 (1,000)				9,807 (1,000)		1,0947
		170	9,807 (1,000)				9,807 (1,000)		1,0900
		180	9,807 (1,000)				9,807 (1,000)		1,0857
		190	9,807 (1,000)				9,807 (1,000)		1,0818
		200	9,807 (1,000)				9,807 (1,000)		1,0783
Примечания:
λ		- длина загружения линии влияния;
a		- коэффициент, определяющий положение вершины линии влияния;
a = a₀ / l , где a₀			- расстояние от вершины до ближайшего конца линии
влияния. Для промежуточных значений α							величину нагрузки		k_c следует
определять по интерполяции.

3. КОЭФФИЦИЕНТ НАДЕЖНОСТИ n _{k [2]}

Длина загружения	Коэффициент n_k
λ, м	Коэффициент n_k
λ, м

λ <50	1,15- λ *0.001
50<λ <50	1,10- (λ -50)*0.0005
λ >=150	1,05

4. МАССА БАЛОК ПРОЕЗЖЕЙ ЧАСТИ [2]

Длина панели	Масса продольных
Длина панели	балок проезжей части
d, м	p₁, кН/м пути
	p₁, кН/м пути
5,5	7,2
7,7	7,5
8,25	7,6
11
11	8,0

	5 . МАССА МЕТАЛЛА ПРОЛЕТНЫХ СТРОЕНИЙ [2]
	Масса металла пролетных строений p₁ (кН/м пути) по годам расчетных норм
Расчетный пролет
L_p, м
L_p, м	1884	1896	1907	1925
	1884	1896	1907	1925
44	25	26	27	31
55	28	30	33	34

66	32	35	37	36
77	34	38	42	44
88	36	43	46	48
110	45	50	53	62

Приложение 6[2]


		Параметры A _з

λ, м	Аз		Λ, м		Аз
λ, м	а=0	а=0.5	Λ, м	а=0		а=0.5

3	3,07	4,01	11	7,26		9,49

4	3,90	5,10	15	8,99		11,74

5	4,53	5,92	20	11,28		14,74

6	5,06	6,60	25	13,70		17,88

7	5,54	7,23	30	16,22		21,18

8	5,98	7,81	35	18,76		24,49

9	6,42	8,39	40	21,32		27,84

10	6,84	8,94	45	23,84		31,13

Примечание. Промежуточные значения параметра				принимаются по

интерполяции.

7. МАССА МОСТОВОГО ПОЛОТНА [2]

	Масса мостового
Тип мостового полотна	Полотна
	p₂, кН/м пути


Мостовые брусья	7,0
Мостовые брусья	7,0
без тротуаров
без тротуаров

Мостовые брусья	9,0


тротуары деревянные
тротуары деревянные

Мостовые брусья	11,0


тротуары из ж/б плит

Безбалластные ж/б плиты	16,0
без тротуаров

Безбалластные ж/б плиты	20,0
тротуары из ж/б плит

8. ЛИНИИ ВЛИЯНИЯ И ПРАВИЛА ИХ ЗАГРУЖЕНИЯ [2]

Элементы

Схема фермы, линии влияния

фермы

Н 0

В1-3

а₁

b₁

a₁

b₁

а₁

Н2-4

λ₁

λ₂

λ₁

a₂

В1-Н2

− α

Ω₁

Ω₂

^λ2

b₂

1 − α

λ₁

λ₂

a₂

^λ1

Ω₂

− α

Н2-В3

^λ2

b₂

Ω₁

–

1− α

a₁

b₂

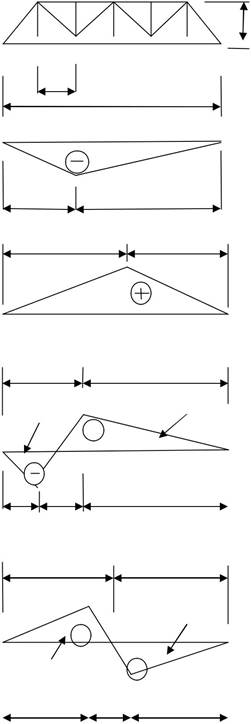
Ω

		Ω =	a₁b₁
		Ω =	2H
		Ω =	a₁b₁
		Ω =	2H
Ω₁	= −		a₂²
Ω₁	= −	2(1 − α )L sin α ₀
		2(1 − α )L sin α ₀
Ω ₂	= +		b²
Ω ₂	= +		2
			2

2(1 − α )L sinα ₀

Ω₁	= +		a₂²
Ω₁	= +	2(1	− α )L sin α ₀
		2(1	− α )L sin α ₀
Ω ₂	= −		b₂²
Ω ₂	= −	2(1	− α )L sinα ₀
		2(1	− α )L sinα ₀

Примечания:

1. Для поясов от постоянной и временной нагрузки Ω_p = Ω_k = Ω.

2. Для раскосов от постоянной нагрузки Ω_p = Ω₁ + Ω₂ (со своими знаками); от временной нагрузки принимается дважды: Ω_k = Ω₁ и Ω_k = Ω_2.

3. В формулы (2.1)–(2.5) подставляются абсолютные значения величин Ω_p и Ω_k; значение допус-каемой нагрузки k подсчитывается дважды и принимается меньшее ее значение.

9. ТАБЛИЦА КЛАССОВ НАГРУЗКИ [3]

Перспективный полувагон грузоподъемностью 151 т

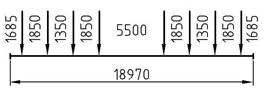
	α=0,0		α=0,5
Длина линии	Эквивалентная нагрузка,		Эквивалентная нагрузка,
влияния, м	Эквивалентная нагрузка,	Класс	Эквивалентная нагрузка,	Класс
влияния, м	тс/м	Класс	тс/м	Класс
	тс/м		тс/м

1	50,00	10,00	50,00	10,00
2	33,13	10,64	25,00	9,17
3	25,84	10,49	18,34	8,51
4	23,28	10,52	17,50	9,04
5	20,90	10,06	17,20	9,47
6	19,31	9,71	16,11	9,26
7	18,27	9,51	15,51	9,23
8	17,11	9,16	15,00	9,18
9	16,35	8,97	14,32	8,98
10	15,74	8,84	13,60	8,73
12	15,14	8,85	12,77	8,53
14	14,83	8,98	12,12	8,39
16	14,48	9,07	12,01	8,59
18	13,91	8,98	11,83	8,72
20	13,40	8,90	11,58	8,79
25	12,81	9,07	11,04	8,93
30	12,42	9,30	10,86	9,29
35	12,27	9,62	10,60	9,50
40	11,96	9,76	10,58	9,87
45	11,82	9,98	10,67	10,30
50	11,69	10,16	10,67	10,60
60	11,49	10,44	10,65	10,65
70	11,37	10,65	10,59	10,59
80	11,26	10,76	10,56	10,56
90	11,19	10,86	10,58	10,58
100	11,12	10,90	10,58	10,58
110	11,08	10,93	10,55	10,55
120	11,03	10,93	10,56	10,56
130	11,00	10,93	10,57	10,57
140	10,96	10,92	10,56	10,56
150	10,94	10,94	10,55	10,55
160	10,91	10,91	10,56	10,56
170	10,89	10,89	10,56	10,56
180	10,87	10,87	10,56	10,56
190	10,85	10,85	10,55	10,55

Восьмиосный полувагон габарита Т_пр

	α=0,0		Α=0,5
Длина линии	Эквивалентная нагрузка,		Эквивалентная нагрузка,
влияния, м	Эквивалентная нагрузка,	Класс	Эквивалентная нагрузка,	Класс
влияния, м	тс/м	Класс	тс/м	Класс
	тс/м		тс/м

1	44,00	8,80	44,00	8,80
2	29,15	9,36	22,00	8,07
3	22,73	9,22	16,13	7,48
4	20,49	9,26	15,40	7,95
5	18,39	8,85	15,14	8,33
6	16,99	8,55	14,18	8,15
7	16,07	8,37	13,65	8,12
8	15,33	8,21	13,20	8,08
9	14,83	8,14	12,71	7,97
10	14,59	8,19	12,50	8,02
12	14,16	8,28	11,73	7,84
14	13,78	8,35	11,76	8,14
16	13,30	8,33	11,55	8,26
18	12,68	8,19	11,30	8,33
20	12,20	8,11	10,91	8,28
25	11,63	8,24	10,02	8,11
30	11,33	8,48	9,73	8,32
35	11,15	8,75	9,54	8,55
40	10,85	8,86	9,53	8,89
45	10,70	9,04	9,61	9,28
50	10,62	9,23	9,65	9,58
60	10,41	9,46	9,62	9,62
70	10,31	9,65	9,52	9,52
80	10,19	9,74	9,52	9,52
90	10,13	9,83	9,56	9,56
100	10,05	9,85	9,53	9,53
110	10,01	9,87	9,50	9,50
120	9,96	9,87	9,52	9,52
130	9,93	9,87	9,53	9,53
140	9,89	9,85	9,51	9,51
150	9,87	9,87	9,50	9,50
160	9,85	9,85	9,51	9,51
170	9,82	9,82	9,51	9,51
180	9,81	9,81	9,50	9,50
190	9,79	9,79	9,50	9,50
200	9,78	9,78	9,51	9,51

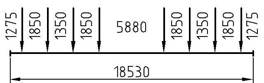
Двадцативосьмиосный сочлененный транспортер грузоподъ-

емностью 400 т (тип 3996)

6.9.47.1. Один транспортер при длине перевозимого груза 15 м

Длина		α=0,0			α=0,5
линии	Эквивалентная	Класс		Эквивалентная	Класс
влияния,	Эквивалентная	с динами-	без дина-	Эквивалентная	с динами-	без дина-
влияния,	нагрузка, тс/м	с динами-	без дина-	нагрузка, тс/м	с динами-	без дина-
м	нагрузка, тс/м	кой	Мики	нагрузка, тс/м	кой	мики
м		кой	Мики		кой	мики
1	50,00	10,00	6,33	50,00	10,00	6,33
2	29,50	9,47	6,06	25,00	9,17	5,87
3	24,50	9,94	6,43	18,02	8,36	5,41
4	22,07	9,98	6,52	18,18	9,39	6,14
5	20,99	10,11	6,67	16,79	9,24	6,10
6	20,21	10,17	6,78	16,97	9,75	6,50
7	19,40	10,10	6,79	16,85	10,02	6,74
8	18,88	10,11	6,86	16,25	9,94	6,75
9	18,56	10,19	6,97	16,45	10,32	7,06
10	18,32	10,29	7,09	16,33	10,48	7,23
12	17,88	10,45	7,32	16,19	10,81	7,57
14	17,51	10,61	7,53	15,93	11,03	7,83
16	17,24	10,80	7,76	15,84	11,33	8,14
18	17,05	11,01	8,01	15,75	11,62	8,45
20	16,82	11,18	8,22	15,63	11,87	8,73
25	15,57	11,03	8,31	14,82	11,99	9,03
30	14,34	10,73	8,26	13,76	11,77	9,05
35	13,23	10,38	8,13	12,71	11,39	8,92
40	12,30	10,04	7,99	11,72	10,93	8,70
45	11,54	9,75	7,86	10,85	10,47	8,45
50	11,34	9,85	8,04	10,13	10,06	8,21
60	11,16	10,14	8,45	9,07	9,07	7,56
70	10,75	10,07	8,53	8,70	8,70	7,37
80	10,26	9,81	8,43	8,66	8,66	7,44
90	9,77	9,49	8,25	8,46	8,46	7,36
100	9,31	9,13	8,02	8,20	8,20	7,20
110	8,94	8,82	7,81	7,92	7,92	7,02
120	8,64	8,56	7,65	7,62	7,62	6,80
130	8,37	8,32	7,48	7,35	7,35	6,61
140	8,16	8,13	7,35	7,12	7,12	6,44
150	7,92	7,92	7,20	6,92	6,92	6,29
160	7,67	7,67	7,01	6,74	6,74	6,16
170	7,42	7,42	6,81	6,58	6,58	6,04
180	7,17	7,17	6,60	6,43	6,43	5,92
190	6,94	6,94	6,42	6,28	6,28	5,81
200	6,72	6,72	6,23	6,12	6,12	5,68

				10. КОЭФФИЦИЕНТ φ

λ	0	10	20	30	40	50	60	70	80	90	100

φ	0,93	0,92	0,90	0,88	0,85	0,82	0,78	0,74	0,69	0,63	0,56


λ	110	120	130	140	150	160	170	180	190	200

φ	0,49	0,43	0,38	0,34	0,31	0,28	0,25	0,23	0,21	0,19

Гибкость элемента λ определяется в двух плоскостях (при изгибе в плоскости фермы и при изгибе из плоскости фермы), принимается наибольшее значение из всех рассчитанных по формуле:

λ = l₀/r ,

где l₀ – свободная длина элемента, см, принимается:

– для элементов поясов (в обеих плоскостях) равной длине панели фермы;

– для раскосов принимается два значения:

l₀ l₀	=		h
					– при изгибе в плоскости фермы, см;
					– при изгибе в плоскости фермы, см;
			cosα ₀
l₀	=	0,8		h		– при изгибе из плоскости фермы, см;
l₀	=	0,8		cosα ₀		– при изгибе из плоскости фермы, см;

h – расчетная высота фермы пролетного строения, см; α₀ – угол наклона раскоса к поясу фермы;

r = ^I ^бр – радиус инерции сечения элемента, см;

^Fбр

I_бр – момент инерции брутто сечения элемента, см⁴; F_бр – площадь сечения брутто, см².

Значения радиуса инерции (r _x и r _y) и момента инерции брутто сечения (I _x_,бр и I _y_,бр) определяются относительно обеих осей, перпендикулярных плоскостям изгиба (приложение 11).

Дата: 2019-02-02, просмотров: 248.

⇐ Предыдущая 1 234 5 6 Следующая ⇒