Решение.

Составим экономико-математическую модель задачи (ЭММ) Обозначим через

 x₁ – количество товара 1-го вида, выпускаемое предприятием

 х₂ – количество товара 2-го вида, выпускаемое предприятием;

 x₃ – количество товара 3-го вида, выпускаемое предприятием;

 x₄ – количество товара 4-го вида, выпускаемое предприятием.

Тогда х₁, х₂, х₃, х₄ – план работы предприятия, а выражение

                 (30х₁ + 25х₂ + 56х₃ + 48х₄) – реализуемая прибыль.

      По условию задачи эта прибыль должна быть максимальной, т. е.

                              max(30х₁ + 25х₂ + 56х₃ + 48х₄)                           (1).

Теперь учтём сырьё, которое идёт на производство товара.

Выражение  (3х₁ + 5х₂ + 2х₃ + 4х₄)    показывает, сколько расходуется сырья на изготовление товара.

         По условию задачи              3х₁ + 5х₂ + 2х₃ + 4х₄≤ 6000.

Учтём теперь рабочую силу, которая идёт на производство товара. Выражение              (22х₁ + 14х₂ + 18х₃ + 30х₄)        показывает, сколько идёт рабочих часов на изготовление товара.

          По условию задачи                22х₁ + 14х₂ + 18х₃ + 30х₄ ≤ 4000.

Теперь учтём оборудование, которое используется при производстве товара.

Выражение (10х₁ + 14х₂ + 8х₃ + 16х₄) показывает, сколько расходуется станко-часов на изготовление товара.

           По условию задачи 10х₁ + 14х₂ + 8х₃ + 16х₄ ≤ 1280.

Так как переменные х₁, х₂, х₃, х₄ имеют экономический смысл, то будем рассматривать их значения только неотрицательными.

Теперь запишем ЭММ задачи

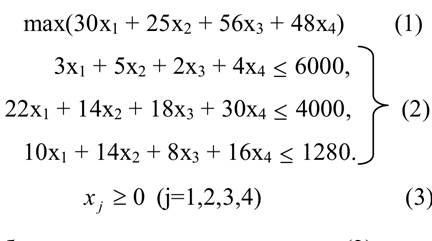
    Здесь выражение (1) – цель работы предприятия, неравенства (2) – ограничения на ресурсы, а неравенства (3) – условия неотрицательности на переменные.

Рассмотрим другую задачу.

Задача 2. При составлении суточного рациона кормления скота можно использовать свежее сено (не более 50 кг) и силос (не более 85 кг). Рацион должен обладать определённой питательностью (число кормовых единиц не менее 30) и содержать питательные вещества: белок (не менее 1 кг), кальций (не менее 100 г) и фосфор (не менее 80 г).

В таблице приведены данные о содержании указанных компонентов в 1 кг каждого продукта питания и себестоимость этих продуктов.

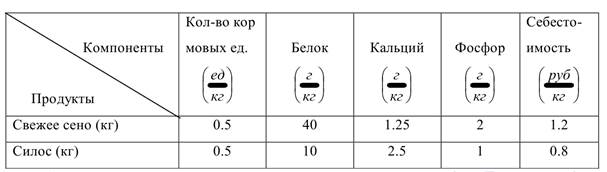
Какой суточный рацион питания скота нужно составить, чтобы стоимость его была минимальной?                                      

Решение.

Обозначим через х₁ – количество свежего сена в рационе, х₂ – количество силоса в рационе.

Тогда х₁, х₂ – суточный рацион кормления скота, а выражение (1.2х₁ + 0.8х₂) его стоимость.

          Но по условию задачи эта стоимость должна быть минимальной, т. е.

min(1.2х₁ + 0.8х₂).

    Теперь учтём условия питательности рациона. Выражение (0.5х₁ + 0.5х₂) учитывает количество кормовых единиц в рационе.

   По условию задачи                        0.5х₁ + 0.5х₂ ≥30.

   Выражение (40х₁ + 10х₂) учитывает количество белка в рационе.

    По условию задачи                       40х₁ + 10х₂ ≥ 1000.

    Выражение (1.25х₁ + 2.5х₂) учитывает количество кальция в рационе.

     По условию задачи                    1.25х₁ + 2.5х₂ ≥ 100.

      Выражение (2х₁ + х₂) учитывает количество фосфора в рационе.

      По условию задачи                     2х₁ + х₂ ≥ 80.

Так как переменные х₁, х₂ имеют экономический смысл, то будем рассматривать их значения только неотрицательными.

Теперь запишем ЭММ задачи