Экономико-математическая модель задачи (ЭММ).

ЭММ закрытой транспортной задачи.

ЭММ для открытых ТЗ.

Общая постановка транспортной задачи (ТЗ).

Пусть имеется m поставщиков А₁, А₂,..., А_m, которые хранят или производят все однородный продукт соответственно в количествах а₁,а₂,...,а_m. Пусть имеется n потребителей  этого продукта B₁,B₂,...,B_n , которые потребляют его соответственно в количествах b₁,b₂,...,b_n . Известны стоимости перевозок единицы продукта от i − го поставщика к j − му потребителю. Она составляет с_ij . В совокупности элементы с_ij образуют матрицу стоимостей C  размерностью (m х n), т.е.

Матрица стоимостей C

Найти такой план перевозок, чтобы все потребности были удовлетворены, а общая стоимость перевозок была минимальной.

Экономико-математическая модель задачи (ЭММ).

Решение.

Составим экономико-математическую модель задачи (ЭММ). Для этого просуммируем все поставки однородного продукта

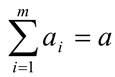
Величину a будем называть общим запасом.

Просуммируем все потребности однородного продукта

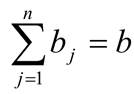
Величину b будем называть общей  потребностью.

Если a = b , то ТЗ будем называть закрытой, в противном случае – открытой.

Будем составлять ЭММ для закрытой ТЗ.

  Обозначим через х_ij количество единиц продукта, перевозимого от i − го поставщика к j − му потребителю. В совокупности элементы х_ij образуют матрицу Х размерностью (m х n), т.е.

Матрица Х и будет планом перевозок.

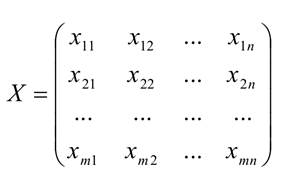
Вычислим сумму произведений элементов матрицы С на соответствующие элементы матрицы Х, получим общую стоимость перевозок, т.е.

Общая стоимость перевозок

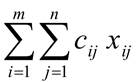
По условию задачи нам нужна минимальная стоимость перевозок, т.е.

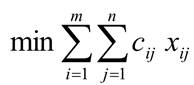
Это выражение, является целью составителя плана перевозок – целевая функция.

 Теперь просуммируем в отдельности элементы строк матрицы Х.

   Рассмотрим сумму элементов i − ой строки

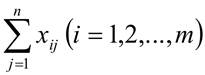
 Эта сумма означает перевозки продукта от i − го поставщика ко всем потребителям. По условию задачи эта сумма должна равняться а_i, т.е.

Получили ограничения на запасы задачи.

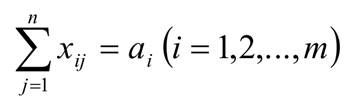
Аналогично, просуммируем в отдельности элементы столбцов матрицы Х. Рассмотрим сумму элементов j − го столбца

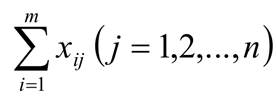
    Эта сумма означает перевозки продукта от всех поставщиков к j − му потребителю. По условию задачи эта сумма должна равняться b_j , т.е.

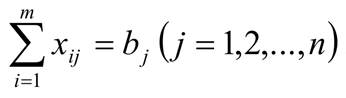
Получили ограничения на потребности задачи.

 Так как элементы матрицы Х имеют содержательный смысл, то будем считать, что все они неотрицательные. В результате получили ЭММ закрытой транспортной задачи: