Лекция 3
Постановка транспортной задачи (ТЗ)
Общая постановка транспортной задачи (ТЗ).
Экономико-математическая модель задачи (ЭММ).
ЭММ закрытой транспортной задачи.
ЭММ для открытых ТЗ.
Общая постановка транспортной задачи (ТЗ).
Пусть имеется m поставщиков А1, А2,..., Аm, которые хранят или производят все однородный продукт соответственно в количествах а1,а2,...,аm. Пусть имеется n потребителей этого продукта B1,B2,...,Bn , которые потребляют его соответственно в количествах b1,b2,...,bn . Известны стоимости перевозок единицы продукта от i − го поставщика к j − му потребителю. Она составляет сij . В совокупности элементы сij образуют матрицу стоимостей C размерностью (m х n), т.е.
Матрица стоимостей C

Найти такой план перевозок, чтобы все потребности были удовлетворены, а общая стоимость перевозок была минимальной.
Экономико-математическая модель задачи (ЭММ).
Решение.
Составим экономико-математическую модель задачи (ЭММ). Для этого просуммируем все поставки однородного продукта
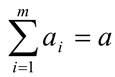
Величину a будем называть общим запасом.
Просуммируем все потребности однородного продукта
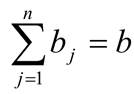
Величину b будем называть общей потребностью.
Если a = b , то ТЗ будем называть закрытой, в противном случае – открытой.
Будем составлять ЭММ для закрытой ТЗ.
Обозначим через хij количество единиц продукта, перевозимого от i − го поставщика к j − му потребителю. В совокупности элементы хij образуют матрицу Х размерностью (m х n), т.е.
Матрица Х и будет планом перевозок.
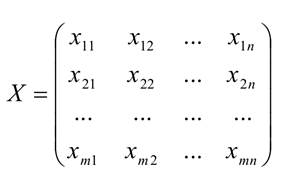
Вычислим сумму произведений элементов матрицы С на соответствующие элементы матрицы Х, получим общую стоимость перевозок, т.е.
Общая стоимость перевозок
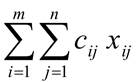
По условию задачи нам нужна минимальная стоимость перевозок, т.е.
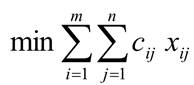
Это выражение, является целью составителя плана перевозок – целевая функция.
Теперь просуммируем в отдельности элементы строк матрицы Х.
Рассмотрим сумму элементов i − ой строки
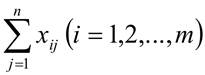
Эта сумма означает перевозки продукта от i − го поставщика ко всем потребителям. По условию задачи эта сумма должна равняться аi, т.е.
Получили ограничения на запасы задачи.
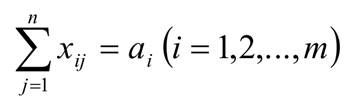
Аналогично, просуммируем в отдельности элементы столбцов матрицы Х. Рассмотрим сумму элементов j − го столбца
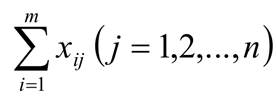
Эта сумма означает перевозки продукта от всех поставщиков к j − му потребителю. По условию задачи эта сумма должна равняться bj , т.е.
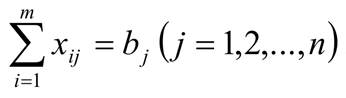
Получили ограничения на потребности задачи.
Так как элементы матрицы Х имеют содержательный смысл, то будем считать, что все они неотрицательные. В результате получили ЭММ закрытой транспортной задачи:
ЭММ для открытых ТЗ.
Рассмотрим ЭММ для открытых ТЗ, когда общий запас не равен общей потребности, т.е. a ≠ b .
Здесь возможны два случая a > b или a < b. Рассмотрим последовательно эти случаи.
Если a > b , то не все поставки будут вывезены. В этом случае ЭММ будет иметь вид:
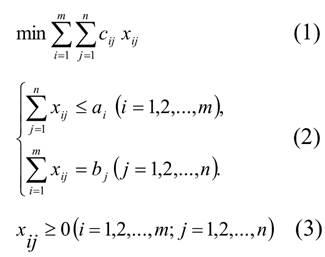
Получили по форме общую ЗЛП. Для сведения её к канонической ЗЛП нужно к левым частям неравенств первой части ограничения (2) прибавить фиктивные переменные xin+1 (i =1,2,...,m). Аналитически это означает, что к матрице Х добавляется (n +1)−ый столбец фиктивных переменных, т.е.
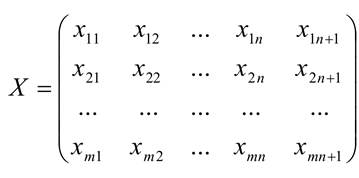
Решение.
Составим экономико-математическую модель задачи (ЭММ) Обозначим через
x1 – количество товара 1-го вида, выпускаемое предприятием
х2 – количество товара 2-го вида, выпускаемое предприятием;
x3 – количество товара 3-го вида, выпускаемое предприятием;
x4 – количество товара 4-го вида, выпускаемое предприятием.
Тогда х1, х2, х3, х4 – план работы предприятия, а выражение
(30х1 + 25х2 + 56х3 + 48х4) – реализуемая прибыль.
По условию задачи эта прибыль должна быть максимальной, т. е.
max(30х1 + 25х2 + 56х3 + 48х4) (1).
Теперь запишем ЭММ задачи
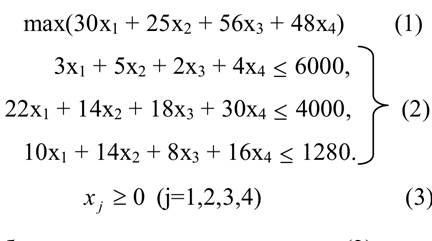
Здесь выражение (1) – цель работы предприятия, неравенства (2) – ограничения на ресурсы, а неравенства (3) – условия неотрицательности на переменные.
Рассмотрим другую задачу.
Задача 2. При составлении суточного рациона кормления скота можно использовать свежее сено (не более 50 кг) и силос (не более 85 кг). Рацион должен обладать определённой питательностью (число кормовых единиц не менее 30) и содержать питательные вещества: белок (не менее 1 кг), кальций (не менее 100 г) и фосфор (не менее 80 г).
Решение.
Обозначим через х1 – количество свежего сена в рационе, х2 – количество силоса в рационе.
Тогда х1, х2 – суточный рацион кормления скота, а выражение (1.2х1 + 0.8х2) его стоимость.
Но по условию задачи эта стоимость должна быть минимальной, т. е.
min(1.2х1 + 0.8х2).
Теперь учтём условия питательности рациона. Выражение (0.5х1 + 0.5х2) учитывает количество кормовых единиц в рационе.
По условию задачи 0.5х1 + 0.5х2 ≥30.
Выражение (40х1 + 10х2) учитывает количество белка в рационе.
По условию задачи 40х1 + 10х2 ≥ 1000.
Выражение (1.25х1 + 2.5х2) учитывает количество кальция в рационе.
По условию задачи 1.25х1 + 2.5х2 ≥ 100.
Выражение (2х1 + х2) учитывает количество фосфора в рационе.
По условию задачи 2х1 + х2 ≥ 80.
Так как переменные х1, х2 имеют экономический смысл, то будем рассматривать их значения только неотрицательными.
Теперь запишем ЭММ задачи

Рассмотрим ещё одну задачу.
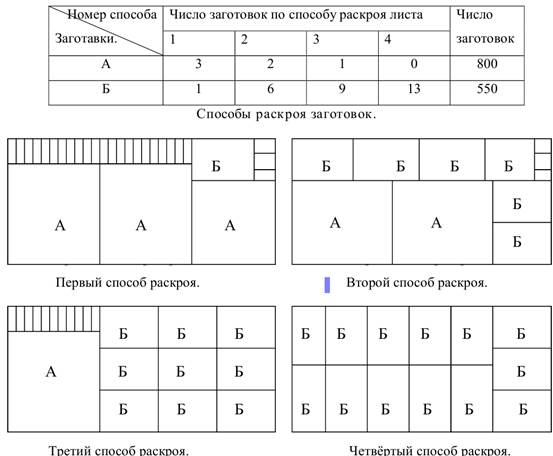
Задача 3. Из листов материала размером 6 м на 13 м нужно выкроить заготовки двух видов А и Б размерами соответственно 4 м на 5 м и 2 м на 3 м в количествах 80штук и 550 штук, израсходовав при этом возможно меньше материала. Для раскроя используются четыре способа. В таблице указано число заготовок каждого вида, получающегося из листа материала.
Решение
Обозначим через х1 – число листов израсходованных по первому способу раскроя, х2 – число листов израсходованных по второму способу раскро х3 – число листов израсходованных по третьему способу раскроя, х4 – число листов израсходованных по четвёртому способу раскроя.
Тогда выражение (х1 + х2 + х3 + х4) – общий расход листов для выкройки заготовок.
По условию задачи он должен быть минимальным, т. е.
min(х1 + х2 + х3 + х4).
Теперь учтём план выпуска заготовок А и Б. Выражение (3х1 + 2х2 + х3) показывает число заготовок вида А, раскроенных четырьмя способами.
По условию задачи 3х1 + 2х2 + х3 ≥ 800.
Выражение (х1 + 6х2 + 9х3 + 13х4 ) показывает число заготовок вида Б, раскроенных четырьмя способами.
По условию задачи х1 + 6х2 + 9х3 + 13х4 ≥ 550.
Так как переменные х1, х2, х3, х4 имеют экономический смысл, то будем рассматривать их значения только неотрицательными.
Теперь запишем ЭММ задачи
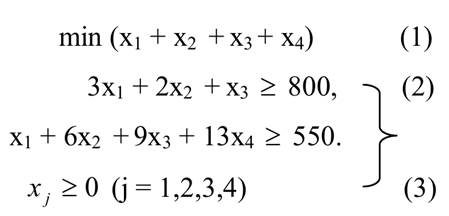
Здесь выражение (1) – цель заготовителя заготовок, неравенства (2) – ограничения на получение количества заготовок вида А и Б, а неравенства (3) – условия неотрицательности на переменные. Ниже мы решим все рассмотренные задачи разными методами.
Лекция 3
Постановка транспортной задачи (ТЗ)
Дата: 2019-02-02, просмотров: 334.