Если a < b, то не все потребности будут удовлетворены. В этом случае ЭММ будет иметь вид:

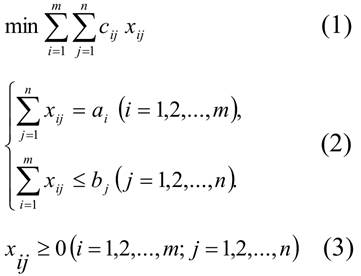
 Получили по форме общую ЗЛП. Для сведения её к канонической ЗЛП нужно к левым частям неравенств второй части ограничения (2) прибавить фиктивные переменные x_m+1j ( j =1,2,...,n).

Аналитически это означает, что к матрице Х добавляется (m +1)− ая строка фиктивных переменных, т.е.

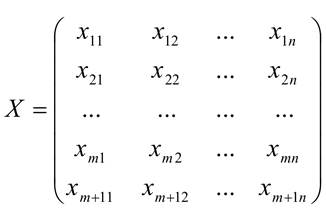
Но каждая строка матрицы Х соответствует поставщику.

Поэтому добавленную (m +1)− ую строку обозначим, как A_m+1 и будем её называть  фиктивным поставщиком. Его поставку a_m+1 определим как разность между общей потребностью и общим запасом, т. е. a_m+1 = b − a. Так как фиктивный запас не вывозится, то формально будем считать, что стоимость перевозок от фиктивного поставщика ко всем потребителям равна нулю, т.е. с_m+1j = 0.

 Аналитически это означает, что к матрице стоимостей С добавляется нулевая строка, т.е.

В результате проделанной процедуры получили снова закрытую ТЗ. Таким образом, любую открытую ТЗ с помощью фиктивных переменных можно свести к закрытой ТЗ. Поэтому в дальнейшем теорию транспортных задач будем рассматривать для закрытых ТЗ

 Пример.

На трёх складах хранится каменный уголь соответственно в количествах 520, 480 и 1000 тонн. Этот уголь нужно доставить в пять пунктов потребления соответственно в количествах 800, 750, 250, 200 и 300 тонн.

В таблице приведены стоимости перевозок одной тонны угля от каждого склада ко всем пунктам потребления.

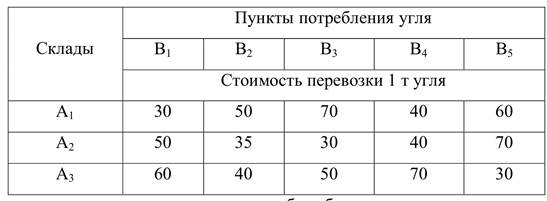
Составить план перевозки угля так, чтобы общие затраты на перевозки были минимальными. Составим ЭММ задачи. По условию задачи подсчитаем общий запас угля на складах. a = 2000 тонн, а общая потребность в угле составит b = 2300 тонн. Так как b > a , то имеем открытую ТЗ. Закроем ТЗ, для этого введём фиктивный четвёртый склад А₄ с запасом угля a₄ = b− a =300 тонн.

Обозначим х_ij количество тонн угля вывозимого из i − го склада в j −ый пункт потребления.

Тогда в совокупности х_ij образуют матрицу Х .

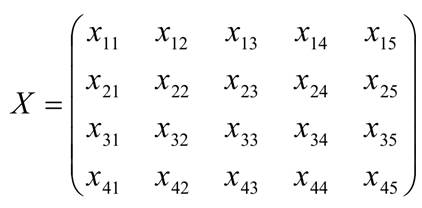
Эта матрица и является планом перевозок угля.

   Так как уголь от фиктивного четвёртого склада не перевозится, то его стоимости перевозок равны нулю, т.е. с_4j = 0. Это означает, что в таблицу стоимостей перевозок добавляется четвёртая нулевая строка. Запишем теперь ЭММ с учётом фиктивных переменных:

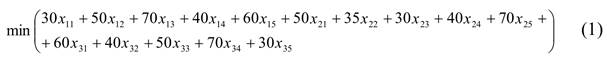
Рассмотрим теперь некоторые конкретные задачи планирования, модели которых сводятся к ЗЛП.

Задача 1. Предприятие располагает ресурсами сырья, рабочей силой и оборудованием, необходимым для производства любого из четырёх видов производимых товаров. Затраты ресурсов на изготовление единицы данного вида товара, прибыль, получаемая предприятием, а также запасы ресурсов указаны в таблице.