Вывод дифференциального уравнения для нестационарного режима в подвижной среде с внутренними источниками теплоты в декартовой системе координат.
Рассмотрим процессы происходящие в подвижной среде с внутренними источниками теплоты (токи Фуко, парообразование, конденсация).
Выделим в подвижной среде элементарный объем в виде прямоугольного параллелепипеда со сторонами dx, dy, dz.

Запишем уравнение теплового баланса для данного случая
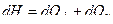 ,
,
где 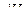 – изменение энтальпии;
– изменение энтальпии;
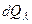 – подводимое количество теплоты;
– подводимое количество теплоты;
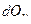 – внутреннее изменение теплоты.
– внутреннее изменение теплоты.
Вывод уравнения производим при следующих условиях:
qv = const (qv – удельная производительность внутренних источников теплоты).
l = const – коэффициент теплопроводности.
Чтобы построить математическую модель этого объекта надо все параметры увязать в одно уравнение.
Изменение энтальпии
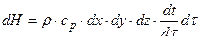 ,
,
где 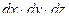 - объем;
- объем; 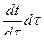 - изменение температуры во времени.
- изменение температуры во времени.
Определяем подводимое количество теплоты
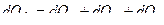
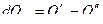
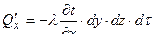 - входящий поток по направлению оси x.
- входящий поток по направлению оси x.
где 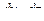 - поверхность, через которую проходит тепловой поток по направлению оси x.
- поверхность, через которую проходит тепловой поток по направлению оси x.
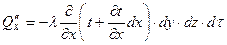 - количество теплоты, выходящее из элементарного параллелепипеда в направлении оси x,
- количество теплоты, выходящее из элементарного параллелепипеда в направлении оси x,
где 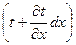 - температурный градиент.
- температурный градиент.
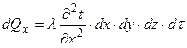 - количество теплоты, аккумулированной элементарным объемом в направлении x .
- количество теплоты, аккумулированной элементарным объемом в направлении x .
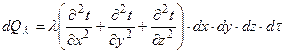 - результирующее количество теплоты.
- результирующее количество теплоты.
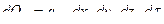
Запишем уравнение теплового баланса:
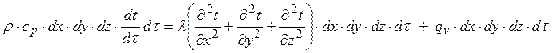
разделим это уравнение на 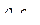 , тогда:
, тогда:
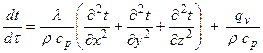 - дифференциальное уравнение второго порядка.
- дифференциальное уравнение второго порядка.
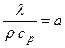 - коэффициент температуропроводности
- коэффициент температуропроводности 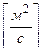 является мерой теплоинерционных свойств материалов. Приводится в таблицах, определяется экспериментально.
является мерой теплоинерционных свойств материалов. Приводится в таблицах, определяется экспериментально.
Температура обладает полным дифференциалом, значит:
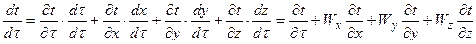
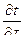 - локальная составляющая изменения температуры во времени;
- локальная составляющая изменения температуры во времени;
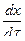 - составляющая скорости по оси x;
- составляющая скорости по оси x;
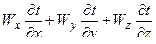 - конвективная составляющая изменения температуры.
- конвективная составляющая изменения температуры.
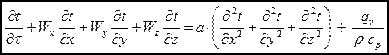
- дифференциальное уравнение теплопроводности в декартовой системе координат или уравнение Фурье-Кирхгофа для подвижной среды при нестационарном режиме.
Частные случаи дифференциального уравнения теплопроводности.
1. Для неподвижной среды (для твердого тела).
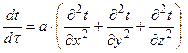 - без внутренних источников теплоты для трехмерного случая.
- без внутренних источников теплоты для трехмерного случая.
где 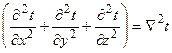 - оператор Лапласа второго порядка (сумма вторых производных).
- оператор Лапласа второго порядка (сумма вторых производных).
2. Дифференциальное уравнение теплопроводности для твердого тела в цилиндрической системе координат.
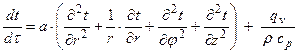
 |
Простейший случай дифференциального уравнения теплопроводности для одномерного стационарного поля.
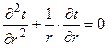
Дата: 2019-02-02, просмотров: 325.