Одна из первых попыток создать уравнение состояния реального газа принадлежит голландскому физику Я. Ван дер Ваальсу (1873г.). На основе, главным образом, умозрительных заключений и идеи непрерывности газообразного и жидкого состояний вещества он предложил уравнение, охватывающее оба эти состояния
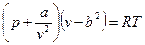 .
.
Это уравнение отличается от уравнения состояния идеального газа тем, что в него входят два дополнительных члена:
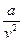 – дополнительное внутреннее давление, вызываемое взаимным приближением молекул;
– дополнительное внутреннее давление, вызываемое взаимным приближением молекул;
b – суммарный объем молекул.
Входящие в уравнение Ван дер Ваальса константы а и b вместе с газовой постоянной R характеризуют индивидуальные свойства вещества.
К сожалению, равнение Ван дер Ваальса учитывает лишь объем молекул и их взаимодействие, что отвечает случаю парных взаимодействий между молекулами, т.е. случаю, результатом которого является лишь обмен энергией между молекулами при соударении. При возрастании плотности газа возрастает число случаев соударений, в которых участвует 3 и более молекул. При этом две и более молекул могут получить равную по величине и направлению скорость, т.е. двигаться как единое целое (ассоциация молекул), а избыток энергии уносится другими молекулами, участвующими в соударении. Таким образом, как бы сокращается число автономных частиц газа, что, естественно, отражается на его поведении.
В результате уравнение Ван дер Ваальса применимо лишь к области сравнительно малых скоростей. Ван дер Ваальсовский газ можно рассматривать как второе после идеального газа приближение к реальному газу.
Уравнение Ван дер Ваальса в принципе неприменимо к области, где вещество обладает резко выраженными свойствами реального газа (вблизи линии насыщения, околокритическая область), и тем более к области жидкости.
В связи с этим предпринималось большое число попыток вывода теоретически обоснованного уравнения состояния справедливого в достаточно широкой области состояний реального газа. Большой шаг вперед в этом направлении был сделан в 1937-1946 гг.независимо друг от друга американским физиком Дж. Майером и советским математиком Н.Н. Боголюбовым. С помощью методов статистической физики они показали, что уравнение состояния реального газа в наиболее общем виде выглядит следующим образом
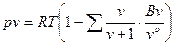 .
.
Это уравнение носит название уравнения Майера-Боголюбова.
Здесь В и  – вириальные коэффициенты, зависящие от потенциальной энергии взаимодействия молекул и температуры газа.
– вириальные коэффициенты, зависящие от потенциальной энергии взаимодействия молекул и температуры газа.
Чисто теоретическими методами они не могут быть вычислены и требуют ряда экспериментальных сведений.
Эта задача обычно оказывается настолько сложной, что более целесообразным путем является получение уравнения состояния в виде интерполяционной формулы, описывающей экспериментальные данные. В инженерной практике определение параметров состояния реального газа, анализ процессов изменения его состояния во многих случаях проводится на основе использования соответствующих таблиц и диаграмм. Их применение мы рассмотрим на примере такого широко используемого реального газа, каким является водяной пар.
Таблицы водяного пара
Имеются три таблицы водяного пара. В двух из них приведены параметры кипящей воды и сухого насыщенного пара, т.е. параметры, характеризующие состояния пара на нижней и верхней пограничных кривых.
Таблица 1
| Рн | Тн | v’ | v’’ | h’ | h’’ | r | s’ | s’’ |
| бар | 0 С | м3/с | м3/с | кДж/кг | кДж/кг | кДж/кг | кДж/кг К | кДж/кг К |
Таблица 2
| Тн | Рн | v’ | v’’ | h’ | h’’ | r | s’ | s’’ |
| 0 С | бар | м3/с | м3/с | кДж/кг | кДж/кг | кДж/кг | кДж/кг К | кДж/кг К |
В таблице 1 приведены указанные выше параметры в функции от давления кипения (насыщения), в таблице 2 – от температуры кипения (насыщения). В этих таблицах приводятся удельные объемы кипения воды (v’) и сухого насыщенного пара (v’’), соответственно их энтальпия (h’, h’’) и энтропия (s’, s’’). Кроме того, в этих таблицах приводится значение скрытой теплоты парообразования (h’’- h’ = r).
Таблица 3
| Р / Т | 0 | 10 | 20 | 30 | 40 |
| 0,01 | V h s | ||||
| 0,02 | V h s | пар | |||
| 0,03 | V h s | жидкость | |||
| 0,04 |
В таблице 3 приведены в функции Р и Т значения v , h и s для воды, не нагретой до кипения, и для перегретого пара.
Таким образом, таблицами не охватывается область влажного насыщенного пара, параметры состояния которого определяются путем расчета с использованием таблиц 1 и 2.
Дата: 2019-02-02, просмотров: 359.