Маркетинг, решение исследовательских задач
Алифанов А.Л., Алифанов Л.А. Маркетинг: Решение исследовательских задач: Учеб. Пособие. Красноярск, ИПЦ КГТУ, 2005. 95 с.
ОГЛАВЛЕНИЕ
Введение
- Проверка статистических гипотез
1.1. Предпосылки использования в маркетинговых исследованиях статистических методов
1.2. Оценка существенности факторов, влияющих на объем производства товара, с помощью непараметрического критерия знаков
1.3. Оценка значимости систематически действующих факторов на результат деятельности фирм с использованием критерия для количества серий
1.4. Анализ компьютерного рынка с позиций однородности объемов продаж лидирующими компаниями
1.5. Вычисление количественной оценки статистической связи между качественными показателями деятельности фирм
1.6. Оценивание резко выделяющихся показателей динамики реального денежного дохода населения
1.7. Проверка однородности выручки, получаемой от российского экспорта основных видов продукции
1.8. Оценка однородности условий маркетинговой деятельности
- Анализ факторов, обуславливающих успех управления маркетингом
2.1. Оценка значимости местонахождения пункта продаж на средние цены автомобилей
2.2. Влияние квалификации специалистов на продолжительность технического обслуживания машин
2.3. Оценка существенности влияния двух факторов и их взаимодействия на показатели маркетинга
- Непараметрические методы исследования в маркетинге
3.1. Экспертные методы оценивания качества товаров и услуг
3.2. Оценивание существенности влияния рейтинга марки товара на прибыль фирм
- Управление запасами
4.1. Термины, постановка задачи
4.2. Расчет оптимального размера партии при равномерном спросе
4.3. Расчет оптимального размера партии в случае модели производственных поставок
- Модели массового обслуживания
5.1. Термины, определения
5.2. Вычисление показателей простейшей очереди
Заключение
Библиографический список
Приложение
ВВЕДЕНИЕ
Маркетинг как вид человеческой деятельности, направленной на удовлетворение нужд и потребностей посредством обмена [7], подвержен влиянию огромного количества факторов демографического, экономического, природного, научно-техничес-кого, политического, культурного характера. Они проявляют себя в случайные моменты времени, в различных сочетаниях, с разной степенью воздействия на эффективность маркетинговой деятельности.
Стратегическое планирование, разработка годовых планов и маркетинговый контроль невозможны без знания рыночной ситуации и формирующих ее факторов макро- и микросреды. Поэтому необходимо выявление наиболее значимых их них с целью построения оптимизационных моделей и написания сценариев, позволяющих осуществлять последовательное и глубокое внедрение на рынки.
Маркетинговая ситуация быстро меняется, уровень значимости факторов, существенных в настоящий момент, через относительно малый промежуток времени может повыситься или снизиться; с развитием рынка на первое место могут выходить качественно новые факторы, коренным образом изменяя условия производства, сбыта и потребления.
В настоящем пособии изложены наиболее простые и эффективные способы, лежащие в основе формирования статистических банков – совокупностей «современных методик статистической обработки информации, позволяющих наиболее полно вскрыть взаимозависимости в рамках подборки данных и установить степень их статистической надежности» [7], а также банков моделей.
Как статистические банки, так и банки оптимизационных и прогнозных моделей требуют постоянного поддержания уровня их надежности за счет совершенствования самих методик и моделей. Изложенные в пособии методики и модели представляют собой фундаментальные знания, на основе которых осуществляется повышение уровня их эффективности.
В первой главе рассмотрены методы и примеры решения задач проверки статистических гипотез при исследовании различных аспектов маркетинговой деятельности с помощью критериев математической статистики. Приведены способы оценивания существенности факторов, влияющих на показатели маркетинга, и значимости систематически действующих факторов на результаты работы фирм. Представлены методы проверки однородности объемов продаж ведущими компаниями, оценки статистической связи между показателями функционирования организаций и резко выделяющихся показателей реального денежного дохода населения. Произведен анализ однородности выручки, получаемой от российского экспорта основных видов продукции, и однородности условий маркетинговой деятельности.
Вторая глава посвящена анализу факторов, обуславлива-ющих эффективность маркетинговой деятельности. Здесь приведены методика и решение задачи с помощью однофакторного дисперсионного анализа: оценка значимости влияния местонахождения пункта продаж на цены автомобилей, а также методика и решение задач с помощью двухфакторного дисперсионного анализа: оценка существенности влияния двух факторов и их взаимодействия на показатели маркетинга.
В третьей главе на примерах проиллюстрированы приемы применения непараметрических методов исследования в маркетинге для количественного оценивания качественных состояний или свойств объектов. Рассмотрены примеры выявления уровня надежности автомобильных узлов, а также уровни эффективности использования различных видов транспорта крупными отправителями. Изложены элементы кластерного анализа в свете оценивания существенности влияния рейтинга марки товара на прибыль фирм.
В четвертой главе изложен один из важнейших аспектов маркетинга – управление запасами. Приведены описание задач теории и способы определения оптимальных размеров партий товара для двух вариантов: в случае равномерного спроса и в случае модели производственных поставок.
В пятой главе рассмотрены понятия теории массового обслуживания и на примерах показаны варианты использования простейших моделей для вычисления основных показателей систем, находящих применение в различных сферах маркетинговой деятельности.
Изложение приведенных в данном пособии методик ориентировано на выполнение расчетов вручную. На практике более удобно осуществлять исследования в специализированных пакетах программ, либо программировать вычислительные алгоритмы самостоятельно, однако, в процессе обучения «ручной» счет предпочтительнее, так как помогает лучше усвоить материал и закрепить его понимание на интуитивном уровне.
УПРАВЛЕНИЕ ЗАПАСАМИ
Термины, постановка задачи
Основной предмет изучения – связь между Q – количеством запаса на складе и временем, для которого рассматривается этот запас [20], т. е. исследуется функция Q = f(t). Затраты, связанные с запасами:
- Организационные издержки – расходы, обусловленные необходимостью оформления и доставки товара; они зависят также от подготовительно-заключительных операций при поступлении товара и подаче заявок и поэтому имеют место при каждом цикле складирования. Если запасы необходимо пополнить, то на склад завозится очередная партия. Издержки, связанные с поставкой, называются организационными. Количество товара, поставляемое на склад, называется размером партии.
- Издержки содержания запасов – это затраты, связанные с хранением (содержание или аренда помещений, естественная порча товара).
- Издержки, связанные с дефицитом (штрафы); если поставки со склада не могут быть выполнены, то возникают дополнительные издержки, обусловленные вынужденным отказом. Это может быть реальный денежный штраф, а может быть просто ухудшение бизнеса в будущем из-за потери разочаровавшихся в поставщике потребителей.
Основная модель управления запасами – определение оптимального размера партии.
В упрощенной модели рассматриваются следующие величины, представленные в табл. 34.
Таблица 34
Исходные данные для вычисления размера партии
| Параметр | Обозначение | Единица измерения | Условия эффективности применения модели |
| 1 | 2 | 3 | 4 |
| Интенсивность спроса | d | Единицы товара в год | Спрос постоянен и непрерывен, весь спрос удовлетворяется |
| Организационные издержки | s | У.е. за 1 партию | Организационные издержки постоянны и не зависят от размера партии |
| Стоимость товара | c | У.е. за единицу товара | Цена постоянна, рассматривается 1 вид товара |
Окончание табл. 34
| 1 | 2 | 3 | 4 |
| Издержки содержания запаса | h | У.е. за единицу товара в год | Стоимость хранения товара в течение года постоянна |
| Размер партии | q | Ед. товара в одной партии | Постоянная величина размера партии, поступление мгновенное, как только уровень запаса становится равным нулю |
Обычно задача управления запасами ставится так: определить размер партии q, при котором годовые затраты будут минимальны. Для условий задачи, сформулированных в табл. 34, зависимость Q = f(t) имеет вид, представляемый графиком (рис. 4.1).
|
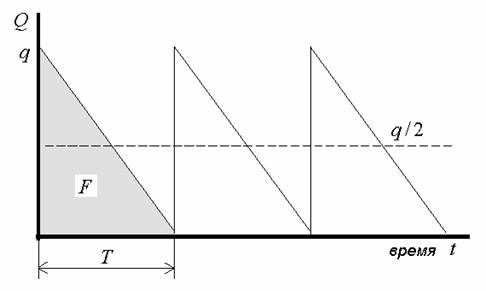
Рис. 4.1. График изменения и пополнения запасов: Q – уровень запаса
(по оси ординат); q – размер поставки (начало цикла); F – площадь под
графиком; T – продолжительность цикла; q/2 – средний уровень запаса
Замечания: 1) чтобы удовлетворить годовой спрос d при размере поставки (партии) q нужно сделать d/q поставок в год;
2) средний уровень запасов q/2 = F/T; F – площадь под графиком за цикл Т.
Уравнение издержек:
С = С1 (организационные издержки) + С2 (стоимость товара) + + С3 (общие издержки содержания запасов).
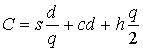 .
.
Оптимальное значение q находят, положив 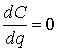 , т. е.
, т. е. 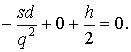
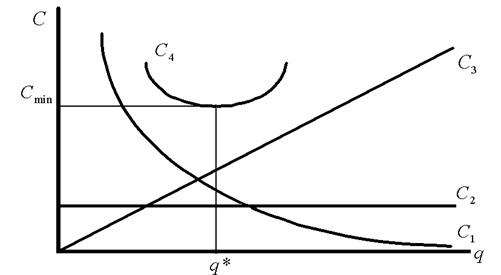
Рис. 4.2. График для определения оптимального размера партии:
С4 – суммарные издержки; Сmin – минимальные суммарные издержки;
q* – оптимальный размер партии
Решая уравнение относительно q – переменной величины, имеем
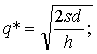
где q* – оптимальный размер партии.
Учитывая, что 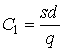 – общие организационные издержки, С2 = сd – стоимость товара, С3 =
– общие организационные издержки, С2 = сd – стоимость товара, С3 = 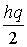 – общие издержки содержания запасов, получим график, приведенный на рис. 4.2.
– общие издержки содержания запасов, получим график, приведенный на рис. 4.2.
ЗАКЛЮЧЕНИЕ
Дисциплина «Маркетинг» занимает одно из важнейших мест в системе подготовки высококвалифицированных инженеров-экономистов в части приобретения ими фундаментальных понятий, знаний терминологии, организации, структуры и методов оптимизации процессов производства, сбыта и потребления товаров.
В практике выполнения дипломных работ собственно маркетинговая тематика является одной из ведущих, помимо этого при выполнении дипломной работы на любую другую тему приходится решать комплекс маркетинговых задач – неотъемлемой составной части экономической проблематики.
Удаленность предприятий Норильского промышленного района от заводов-изготовителей технологического оборудования, машин и материалов предполагает наличие множества вариантов выбора поставщиков, потребителей продукции НПР и видов транспорта, поэтому привитие знаний, умений и навыков исследовательского подхода к решению практических задач является необходимой составляющей процесса обучения.
Кем бы и где бы не работал молодой специалист, он обязательно столкнется с задачами, способы разрешения которых и все основные и необходимые данные приведены в настоящем пособии.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- Большев, Л. Н. Таблицы математической статистики /
Л. Н. Большев, Н. В. Смирнов. М.: Наука, 1983. 416 с. - Вознесенский, В. А. Статистические методы планирования эксперимента в технико-экономических исследованиях /
В. А. Вознесенский. М.: Статистика, 1981. 263 с. - Вентцель, Е. С. Теория вероятностей / Е. С. Вентцель. М.: Наука, 1969. 576 с.
- Вагнер, Г. Основы исследования операций / Г. Вагнер. М.: Наука, 1972. 420 с.
- Гмурман, В. Е. Теория вероятностей и математическая статистика / В. Е. Гмурман. М.: Высш. шк., 1977. 479 с.
- Голубков, Е. П. Основы маркетинга: Учебник / Е. П. Голубков. М.: Изд-во «Финпресс», 1999. 656 с.
- Котлер, Ф. Основы маркетинга / Ф. Котлер. М.: Бизнес-книга, 1995. 702 с.
- Красильников, В. В. Статистика объектов нечисловой природы / В. В. Красильников. Наб. Челны: Изд-во Камского политехнического института, 2001. 144 с.
- Саати, Т. Математические методы исследования операций/ Т. Саати. М.: Воениздат, 1963. 219 с.
- Алифанов, А. Л. Северные регионы. Потребность в ремонтных комплектах для автомобилей / А. Л. Алифанов // Автомобильная промышленность. 1997. № 12. С. 20–22.
- Бушуева, Л. И. Методы прогнозирования объема продаж / Л. И. Бушуева // Маркетинг в России и за рубежом. 2002. № 1. С. 15–29.
- Виноградов, В. А. Некоторые вопросы ценообразования на основе спроса на рынке бытовой мебели Российской Федерации / В. А. Виноградов // Маркетинг в России и за рубежом. 2002. № 5. С. 77–85.
- Канунников, С. И. Автобум по-русски / С. И. Канунников, Д. С. Канунников // Маркетинг в России и за рубежом. 2002. № 2. С. 108–114.
- Каплина, О. В. Оценка конкурентоспособности массового товара (на примере пива) / О. В. Каплина // Маркетинг в России и за рубежом. 2001. № 4. С. 28–48.
- Кац, И. С. Компьютерный рынок: настоящее и ближайшее будущее / И. С. Кац, Л. В. Тихонова // Маркетинг в России и за рубежом. 2001. № 3. С. 35–41.
- Ларионов, В. Г. Проблема фальсификации товарной продукции в России и за рубежом / В. Г. Ларионов, М. Н. Скрыпников // Маркетинг в России и за рубежом. 2001. № 1. С 114–119.
- Савин, В. А. Роль субъектов Российской Федерации в формировании товарной структуры экспорта страны / В. А. Савин, В. А. Сковорода // Маркетинг в России и за рубежом. 2002. № 3. С. 42–52.
- Чуровский, С. Р. Продуктовый портфель мясоперерабатывающего предприятия / С. Р. Чуровский, Г. В. Сафонов // Маркетинг в России и за рубежом. 2002. № 4. С. 19–31.
- Шекова, Е. Л. Маркетинговое исследование рынка культурных услуг в России и за рубежом / Е. Л. Шекова // Маркетинг в России и за рубежом. 2002. № 6. С. 23–29.
- Тернер, Д. Вероятность, статистика и исследование операций / Д. Тернер. М.: Статистика, 1976. 431 с.
ПРИЛОЖЕНИЕ
Таблицы математической статистики [1]
Таблица 1
Критерий знаков. Доверительные пределы для медианы
| μ | Уровень значимости α | μ | Уровень значимости α | ||
| 0,10 | 0,05 | 0,10 | 0,05 | ||
| 0 | 4 | 5 | 26 | 64 | 67 |
| 1 | 7 | 8 | 27 | 66 | 69 |
| 2 | 9 | 11 | 28 | 68 | 71 |
| 3 | 12 | 13 | 29 | 70 | 74 |
| 4 | 14 | 16 | 30 | 72 | 76 |
| 5 | 17 | 18 | 31 | 75 | 78 |
| 6 | 19 | 21 | 32 | 77 | 80 |
| 7 | 21 | 23 | 33 | 79 | 82 |
| 8 | 24 | 26 | 34 | 81 | 85 |
| 9 | 26 | 28 | 35 | 83 | 87 |
| 10 | 28 | 30 | 36 | 85 | 89 |
| 11 | 31 | 33 | 37 | 87 | 91 |
| 12 | 33 | 35 | 38 | 90 | 93 |
| 13 | 35 | 37 | 39 | 92 | 96 |
| 14 | 37 | 40 | 40 | 94 | 98 |
| 15 | 39 | 42 | 41 | 96 | 100 |
| 16 | 42 | 44 | 42 | 98 | 102 |
| 17 | 44 | 47 | 43 | 100 | 104 |
| 18 | 46 | 49 | 44 | 102 | 106 |
| 19 | 48 | 51 | 45 | 105 | 109 |
| 20 | 51 | 53 | 46 | 107 | 111 |
| 21 | 53 | 56 | 47 | 109 | 113 |
| 22 | 55 | 58 | 48 | 111 | 115 |
| 23 | 57 | 60 | 49 | 113 | 117 |
| 24 | 59 | 62 | 50 | 115 | 119 |
| 25 | 62 | 65 | 51 | 117 | 122 |
<з>Таблица предназначена для проверки гипотезы р = 0,5 в последовательности независимых испытаний. Если в результате наблюдений было установлено, что количество «положительных исходов» равно μ, то для проверки гипотезы р = 0,5 по таблице следует найти критические значения N(Q, μ) и N(Q, n – μ), соответствующие заданному уровню значимости α.
1. При альтернативе {p < 0,05} основная гипотеза отвергается с уровнем значимости α, если n ≥ N(α, μ).
2 . При альтернативе {p > 0,5} основная гипотеза p = 0,5 отвергается с уровнем значимости α, если n ≥ N(α, n – μ).
3. При двусторонней альтернативе {p ≠ 0,5} основная гипотеза p = 0,5 отвергается с уровнем значимости 2α, если n ≥ N (α, min (μ, n – μ)).
Таблица 2
Критические значения для количества серий
| m | n | Уровни значимости | m | n | Уровни значимости | ||
| 0,10 | 0,05 | 0,10 | 0,05 | ||||
| 2 | 2 | 1 5 | 1 5 | 5 | 5 | 3 9 | 2 10 |
| 3 | 1 6 | 1 6 | 6 | 3 10 | 3 10 | ||
| 4 | 1 6 | 1 6 | 7 | 3 10 | 3 11 | ||
| 5 | 1 6 | 1 6 | 8 | 3 11 | 3 11 | ||
| 6 | 1 6 | 1 6 | 9 | 4 11 | 3 12 | ||
| 7 | 1 6 | 1 6 | 10 | 4 11 | 3 12 | ||
| 8 | 2 6 | 1 6 | 11 | 4 12 | 4 12 | ||
| 9 | 2 6 | 1 6 | 12 | 4 12 | 4 12 | ||
| 10 | 2 6 | 1 6 | 13 | 4 12 | 4 12 | ||
| 12 | 2 6 | 2 6 | 14 | 5 12 | 4 12 | ||
| 20 | 2 6 | 2 6 | 18 | 5 12 | 5 12 | ||
| 3 | 3 | 1 7 | 1 7 | 20 | 5 12 | 5 12 | |
| 4 | 1 7 | 1 8 | 6 | 6 | 3 11 | 3 11 | |
| 5 | 2 8 | 1 8 | 7 | 4 11 | 3 12 | ||
| 6 | 2 8 | 2 8 | 8 | 4 12 | 3 12 | ||
| 7 | 2 8 | 2 8 | 9 | 4 12 | 4 13 | ||
| 8 | 2 8 | 2 8 | 10 | 5 12 | 4 13 | ||
| 9 | 2 8 | 2 8 | 11 | 5 13 | 4 13 | ||
| 10 | 3 8 | 2 8 | 12 | 5 13 | 4 13 | ||
| 11 | 3 8 | 2 8 | 13 | 5 13 | 5 14 | ||
| 15 | 3 8 | 3 8 | 14 | 5 13 | 5 14 | ||
| 16 | 3 8 | 3 8 | 15 | 6 14 | 5 14 | ||
| 17 | 3 8 | 3 8 | 20 | 6 14 | 6 14 | ||
| 20 | 3 8 | 3 8 | 7 | 7 | 4 12 | 3 13 | |
| 4 | 4 | 2 8 | 1 9 | 8 | 4 13 | 4 13 | |
| 5 | 2 9 | 2 9 | 9 | 5 13 | 4 14 | ||
| 6 | 3 9 | 2 9 | 10 | 5 13 | 5 14 | ||
| 7 | 3 9 | 2 10 | 11 | 5 14 | 5 14 | ||
| 8 | 3 10 | 3 10 | 12 | 6 14 | 5 14 | ||
| 9 | 3 10 | 3 10 | 13 | 6 14 | 5 15 | ||
| 11 | 3 10 | 3 10 | 14 | 6 14 | 5 15 | ||
| 12 | 4 10 | 3 10 | 15 | 6 15 | 5 15 | ||
| 13 | 4 10 | 3 10 | 16 | 6 15 | 6 16 | ||
| m | n | Уровни значимости | m | n | Уровни значимости | ||
| 0,10 | 0,05 | 0,10 | 0,05 | ||||
| 16 | 4 10 | 4 10 | 17 | 7 15 | 6 16 | ||
| 20 | 4 10 | 4 10 | 20 | 7 15 | 6 16 | ||
| 8 | 8 | 5 13 | 4 14 | 11 | 18 | 10 20 | 9 20 |
| 9 | 5 14 | 5 14 | 19 | 10 20 | 9 21 | ||
| 10 | 6 14 | 5 15 | 20 | 10 20 | 9 21 | ||
| 11 | 6 15 | 5 15 | 12 | 12 | 8 18 | 7 19 | |
| 12 | 6 15 | 6 16 | 13 | 9 18 | 8 19 | ||
| 14 | 7 16 | 6 16 | 14 | 9 19 | 8 20 | ||
| 17 | 7 16 | 7 17 | 15 | 9 19 | 8 20 | ||
| 18 | 8 16 | 7 17 | 16 | 10 20 | 9 21 | ||
| 19 | 8 16 | 7 17 | 17 | 10 20 | 9 21 | ||
| 20 | 8 17 | 7 17 | 18 | 10 21 | 9 21 | ||
| 9 | 9 | 6 14 | 5 15 | 19 | 10 21 | 10 22 | |
| 10 | 6 15 | 5 16 | 20 | 11 21 | 10 22 | ||
| 11 | 6 15 | 6 16 | 13 | 13 | 9 19 | 8 20 | |
| 12 | 7 16 | 6 16 | 14 | 9 20 | 9 20 | ||
| 13 | 7 16 | 6 17 | 15 | 10 20 | 9 21 | ||
| 14 | 7 17 | 7 17 | 16 | 10 21 | 9 21 | ||
| 15 | 8 17 | 7 18 | 17 | 10 21 | 10 22 | ||
| 17 | 8 17 | 7 18 | 18 | 11 21 | 10 22 | ||
| 18 | 8 18 | 8 18 | 19 | 11 22 | 10 23 | ||
| 19 | 8 18 | 8 18 | 20 | 11 22 | 10 23 | ||
| 20 | 9 18 | 8 18 | 14 | 14 | 10 20 | 9 21 | |
| 10 | 10 | 6 16 | 6 16 | 15 | 10 21 | 9 22 | |
| 11 | 7 16 | 6 17 | 16 | 11 21 | 10 22 | ||
| 12 | 7 17 | 7 17 | 17 | 11 22 | 10 23 | ||
| 13 | 8 17 | 7 18 | 18 | 11 22 | 10 23 | ||
| 14 | 8 17 | 7 18 | 19 | 12 23 | 11 23 | ||
| 15 | 8 18 | 7 18 | 20 | 12 23 | 11 24 | ||
| 16 | 8 18 | 8 19 | 15 | 15 | 11 21 | 10 22 | |
| 17 | 9 18 | 8 19 | 16 | 11 22 | 10 23 | ||
| 18 | 9 19 | 8 19 | 17 | 11 22 | 11 23 | ||
| 19 | 9 19 | 8 20 | 18 | 12 23 | 11 24 | ||
| 20 | 9 19 | 9 20 | 19 | 12 23 | 11 24 | ||
| 11 | 11 | 7 17 | 7 17 | 20 | 12 24 | 12 25 | |
| 12 | 8 17 | 7 18 | 16 | 16 | 11 23 | 11 23 | |
| 13 | 8 18 | 7 19 | 17 | 12 23 | 11 24 | ||
| 14 | 8 18 | 8 19 | 18 | 12 24 | 11 25 | ||
| 15 | 9 19 | 8 19 | 19 | 13 24 | 12 25 | ||
| 16 | 9 19 | 8 20 | 20 | 13 25 | 12 25 | ||
| 17 | 9 19 | 9 20 | – | ||||
Таблица 3
Критические значения статистики W-критерия Вилкоксона
| m | n | Уровни значимости | m | n | Уровни значимости | ||||||
| 0,10 | 0,05 | 0,10 | 0,05 | ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||||
| 1 | 9 | 1 | – | 3 | 14 | 16 | 13 | ||||
| 18 | 1 | – | 15 | 16 | 13 | ||||||
| 19 | 2 | 1 | 16 | 17 | 14 | ||||||
| 25 | 2 | 1 | 17 | 18 | 15 | ||||||
| 2 | 3 | 3 | – | 18 | 19 | 15 | |||||
| 4 | 3 | – | 19 | 20 | 16 | ||||||
| 5 | 4 | 3 | 20 | 21 | 17 | ||||||
| 6 | 4 | 3 | 21 | 21 | 17 | ||||||
| 7 | 4 | 3 | 22 | 22 | 18 | ||||||
| 8 | 5 | 4 | 23 | 23 | 19 | ||||||
| 9 | 5 | 4 | 24 | 24 | 19 | ||||||
| 10 | 6 | 4 | 25 | 25 | 20 | ||||||
| 11 | 6 | 4 | 4 | 4 | 13 | 11 | |||||
| 12 | 7 | 5 | 5 | 14 | 12 | ||||||
| 13 | 7 | 5 | 6 | 15 | 13 | ||||||
| 14 | 8 | 6 | 7 | 16 | 14 | ||||||
| 15 | 8 | 6 | 8 | 17 | 15 | ||||||
| 16 | 8 | 6 | 9 | 19 | 16 | ||||||
| 17 | 9 | 6 | 10 | 20 | 17 | ||||||
| 18 | 9 | 7 | 11 | 21 | 18 | ||||||
| 19 | 10 | 7 | 12 | 22 | 19 | ||||||
| 20 | 10 | 7 | 13 | 23 | 20 | ||||||
| 21 | 11 | 8 | 14 | 25 | 21 | ||||||
| 22 | 11 | 8 | 15 | 26 | 22 | ||||||
| 23 | 12 | 8 | 16 | 27 | 24 | ||||||
| 24 | 12 | 9 | 17 | 28 | 25 | ||||||
| 25 | 12 | 9 | 18 | 30 | 26 | ||||||
| 3 | 3 | 7 | 6 | 19 | 31 | 27 | |||||
| 4 | 7 | 6 | 20 | 32 | 28 | ||||||
| 5 | 8 | 7 | 21 | 33 | 29 | ||||||
| 6 | 9 | 8 | 22 | 35 | 30 | ||||||
| 7 | 10 | 8 | 23 | 36 | 31 | ||||||
| 8 | 11 | 9 | 24 | 38 | 32 | ||||||
| 9 | 11 | 10 | 25 | 38 | 33 | ||||||
| 10 | 12 | 10 | 5 | 5 | 20 | 19 | |||||
| 11 | 13 | 11 | 6 | 22 | 20 | ||||||
| 12 | 14 | 11 | 7 | 23 | 21 | ||||||
| 13 | 15 | 12 | 8 | 25 | 23 | ||||||
| m | n | Уровни значим. | m | n | Уровни значим. | m | n | Уровни значим. | |||
| 0,10 | 0,05 | 0,10 | 0,05 | 0,10 | 0,05 | ||||||
| 5 | 9 | 27 | 24 | 7 | 9 | 46 | 43 | 9 | 13 | 83 | 78 |
| 10 | 28 | 26 | 10 | 49 | 45 | 14 | 86 | 81 | |||
| 11 | 30 | 27 | 11 | 51 | 47 | 15 | 90 | 84 | |||
| 12 | 32 | 28 | 12 | 54 | 49 | 16 | 93 | 87 | |||
| 13 | 33 | 30 | 13 | 56 | 52 | 17 | 97 | 90 | |||
| 14 | 35 | 31 | 14 | 59 | 54 | 18 | 100 | 93 | |||
| 15 | 37 | 33 | 15 | 61 | 56 | 19 | 103 | 96 | |||
| 16 | 38 | 34 | 16 | 64 | 58 | 20 | 107 | 99 | |||
| 17 | 40 | 35 | 17 | 66 | 61 | 21 | 110 | 102 | |||
| 18 | 42 | 37 | 18 | 69 | 63 | 22 | 113 | 105 | |||
| 19 | 43 | 38 | 19 | 71 | 65 | 23 | 117 | 108 | |||
| 20 | 45 | 40 | 20 | 74 | 67 | 24 | 120 | 111 | |||
| 21 | 47 | 41 | 21 | 76 | 69 | 25 | 123 | 114 | |||
| 22 | 48 | 43 | 22 | 79 | 72 | 10 | 10 | 87 | 82 | ||
| 23 | 50 | 44 | 23 | 81 | 74 | 11 | 91 | 86 | |||
| 24 | 51 | 45 | 24 | 84 | 76 | 12 | 94 | 89 | |||
| 25 | 53 | 47 | 25 | 86 | 78 | 13 | 98 | 92 | |||
| 6 | 6 | 30 | 28 | 8 | 8 | 55 | 51 | 14 | 102 | 96 | |
| 7 | 32 | 29 | 9 | 58 | 54 | 15 | 106 | 99 | |||
| 8 | 34 | 31 | 10 | 60 | 56 | 16 | 109 | 103 | |||
| 9 | 36 | 33 | 11 | 63 | 59 | 17 | 113 | 106 | |||
| 10 | 38 | 35 | 12 | 66 | 62 | 18 | 117 | 110 | |||
| 11 | 40 | 37 | 13 | 69 | 64 | 19 | 121 | 113 | |||
| 12 | 42 | 38 | 14 | 72 | 67 | 20 | 125 | 117 | |||
| 13 | 44 | 40 | 14 | 75 | 69 | 21 | 128 | 120 | |||
| 14 | 46 | 42 | 16 | 78 | 72 | 22 | 132 | 123 | |||
| 15 | 48 | 44 | 17 | 81 | 75 | 23 | 136 | 127 | |||
| 16 | 50 | 46 | 18 | 84 | 77 | 24 | 140 | 130 | |||
| 17 | 52 | 47 | 19 | 87 | 80 | 25 | 144 | 134 | |||
| 18 | 55 | 49 | 20 | 90 | 83 | 11 | 11 | 106 | 100 | ||
| 19 | 57 | 51 | 21 | 92 | 85 | 12 | 110 | 104 | |||
| 20 | 59 | 53 | 22 | 95 | 88 | 13 | 114 | 108 | |||
| 21 | 61 | 55 | 23 | 98 | 90 | 14 | 118 | 112 | |||
| 22 | 63 | 57 | 24 | 101 | 93 | 15 | 123 | 116 | |||
| 23 | 65 | 58 | 25 | 104 | 96 | 16 | 127 | 120 | |||
| 24 | 67 | 60 | 9 | 9 | 70 | 66 | 17 | 131 | 123 | ||
| 25 | 69 | 62 | 10 | 73 | 69 | 18 | 135 | 127 | |||
| 7 | 7 | 41 | 39 | 11 | 76 | 72 | 19 | 139 | 131 | ||
| 8 | 44 | 41 | 12 | 80 | 75 | 20 | 144 | 135 | |||
| m | n | Уровни значим. | m | n | Уровни значим. | m | n | Уровни знач. | |||
| 0,10 | 0,05 | 0,10 | 0,05 | 0,10 | 0,05 | ||||||
| 11 | 20 | 144 | 135 | 14 | 18 | 196 | 187 | 17 | 25 | 314 | 300 |
| 21 | 148 | 139 | 19 | 202 | 192 | 18 | 18 | 291 | 280 | ||
| 22 | 152 | 143 | 20 | 207 | 197 | 19 | 299 | 287 | |||
| 23 | 156 | 147 | 21 | 213 | 202 | 20 | 306 | 294 | |||
| 24 | 161 | 151 | 22 | 218 | 207 | 21 | 313 | 301 | |||
| 25 | 165 | 155 | 23 | 224 | 212 | 22 | 321 | 307 | |||
| 12 | 12 | 127 | 120 | 24 | 229 | 218 | 23 | 328 | 314 | ||
| 13 | 131 | 125 | 25 | 235 | 223 | 24 | 335 | 321 | |||
| 14 | 136 | 129 | 15 | 15 | 200 | 192 | 25 | 343 | 328 | ||
| 15 | 141 | 133 | 16 | 206 | 197 | 19 | 19 | 325 | 313 | ||
| 16 | 145 | 138 | 17 | 212 | 203 | 20 | 333 | 320 | |||
| 17 | 150 | 142 | 18 | 218 | 208 | 21 | 341 | 328 | |||
| 18 | 155 | 146 | 19 | 224 | 214 | 22 | 349 | 335 | |||
| 19 | 159 | 150 | 20 | 230 | 220 | 23 | 357 | 342 | |||
| 20 | 164 | 155 | 21 | 236 | 225 | 24 | 364 | 350 | |||
| 21 | 169 | 159 | 22 | 242 | 231 | 25 | 372 | 357 | |||
| 22 | 173 | 163 | 23 | 248 | 236 | 20 | 20 | 361 | 348 | ||
| 23 | 178 | 168 | 24 | 254 | 242 | 21 | 370 | 356 | |||
| 24 | 183 | 172 | 25 | 260 | 248 | 22 | 378 | 364 | |||
| 25 | 187 | 176 | 16 | 16 | 229 | 219 | 23 | 386 | 371 | ||
| 13 | 13 | 149 | 142 | 17 | 235 | 225 | 24 | 394 | 379 | ||
| 14 | 154 | 147 | 18 | 242 | 231 | 25 | 403 | 387 | |||
| 15 | 159 | 152 | 19 | 248 | 237 | 21 | 21 | 399 | 385 | ||
| 16 | 165 | 156 | 20 | 255 | 243 | 22 | 408 | 393 | |||
| 17 | 170 | 161 | 21 | 261 | 249 | 23 | 417 | 401 | |||
| 18 | 175 | 166 | 22 | 267 | 255 | 24 | 425 | 410 | |||
| 19 | 180 | 171 | 23 | 274 | 261 | 25 | 434 | 418 | |||
| 20 | 185 | 175 | 24 | 280 | 267 | 22 | 22 | 439 | 424 | ||
| 21 | 190 | 180 | 25 | 287 | 273 | 23 | 448 | 432 | |||
| 22 | 195 | 185 | 17 | 17 | 259 | 249 | 24 | 457 | 441 | ||
| 23 | 200 | 189 | 18 | 266 | 255 | 25 | 467 | 450 | |||
| 24 | 205 | 194 | 19 | 273 | 262 | 23 | 23 | 481 | 465 | ||
| 25 | 211 | 199 | 20 | 280 | 268 | 24 | 491 | 474 | |||
| 14 | 14 | 174 | 166 | 21 | 287 | 274 | 25 | 500 | 483 | ||
| 15 | 179 | 171 | 22 | 294 | 281 | 24 | 24 | 525 | 507 | ||
| 16 | 185 | 176 | 23 | 300 | 287 | 25 | 535 | 517 | |||
| 17 | 190 | 182 | 24 | 307 | 294 | 25 | 25 | 570 | 552 | ||
Таблица 4
Критерий исключения резко выделяющихся наблюдений
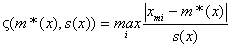
| Число членов вариационного ряда n | ||
Уровни значимости
Число членов вариационного ряда n
Уровни значимости
Таблица 5
Критерии исключения резко выделяющихся наблюдений
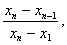
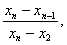
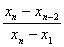
| Число членов вариационного ряда n | Уровни значимости α | Число членов вариационного ряда n | Уровни значимости α | ||
| 0,10 | 0,05 | 0,10 | 0,05 | ||
| 3 | 0,886 | 0,941 | 11 | 0,332 | 0,392 |
| 1,000 | 1,000 | 0,385 | 0,450 | ||
| 1,000 | 1,000 | 0,449 | 0,504 | ||
| Число членов вариационного ряда n | Уровни значимости α | Число членов вариационного ряда n | Уровни значимости α | ||
| 0,10 | 0,05 | 0,10 | 0,05 | ||
| 4 | 0,679 | 0,765 | 12 | 0,318 | 0,376 |
| 0,910 | 0,955 | 0,367 | 0,428 | ||
| 0,935 | 0,967 | 0,429 | 0,481 | ||
| 5 | 0,557 | 0,642 | 15 | 0,285 | 0,338 |
| 0,728 | 0,807 | 0,323 | 0,381 | ||
| 0,782 | 0,845 | 0,382 | 0,430 | ||
| 6 | 0,482 | 0,560 | 20 | 0,252 | 0,300 |
| 0,609 | 0,689 | 0,282 | 0,334 | ||
| 0,670 | 0,736 | 0,333 | 0,372 | ||
| 7 | 0,434 | 0,507 | 24 | 0,234 | 0,281 |
| 0,530 | 0,610 | 0,260 | 0,309 | ||
| 0,596 | 0,661 | 0,309 | 0,347 | ||
| 8 | 0,399 | 0,468 | 30 | 0,215 | 0,260 |
| 0,479 | 0,554 | 0,236 | 0,283 | ||
| 0,545 | 0,607 | 0,285 | 0,322 | ||
| 9 | 0,370 | 0,437 | – | – | – |
| 0,441 | 0,512 | – | – | – | |
| 0,505 | 0,565 | – | – | – | |
| 10 | 0,319 | 0,412 | – | – | – |
| 0,409 | 0,477 | – | – | – | |
| 0,474 | 0,531 | – | – | – | |
Таблица 6
Критерий Аббе
| n | P = 0,05 | n | P = 0,05 | n | P = 0,05 | n | P = 0,05 |
| 4 | 0,3902 | 19 | 0,6417 | 34 | 0,7256 | 49 | 0,7698 |
| 5 | 0,4103 | 20 | 0,6498 | 35 | 0,7292 | 50 | 0,7718 |
| 6 | 0,4451 | 21 | 0,6574 | 36 | 0,7328 | 51 | 0,7739 |
| 7 | 0,4680 | 22 | 0,6645 | 37 | 0,7363 | 52 | 0,7759 |
| 8 | 0,4912 | 23 | 0,6713 | 38 | 0,7396 | 53 | 0,7779 |
| 9 | 0,5121 | 24 | 0,6776 | 39 | 0,7429 | 54 | 0,7799 |
| 10 | 0,5311 | 25 | 0,6836 | 40 | 0,7461 | 55 | 0,7817 |
| 11 | 0,5482 | 26 | 0,6893 | 41 | 0,7491 | 56 | 0,7836 |
| 12 | 0,5638 | 27 | 0,6946 | 42 | 0,7521 | 57 | 0,7853 |
| 13 | 0,5778 | 28 | 0,6996 | 43 | 0,7550 | 58 | 0,7872 |
| 14 | 0,5908 | 29 | 0,7046 | 44 | 0,7576 | 59 | 0,7891 |
| 15 | 0,6027 | 30 | 0,7091 | 45 | 0,7603 | ∞ | 0,7906 |
| 16 | 0,6137 | 31 | 0,7136 | 46 | 0,7628 | – | – |
| 17 | 0,6237 | 32 | 0,7177 | 47 | 0,7653 | – | – |
| 18 | 0,6330 | 33 | 0,7216 | 48 | 0,7676 | – | – |
Таблица 7
Критические точки распределения Стьюдента
| Число степеней свободы k | Уровень значимости α(двусторонняя критическая область) | ||
| 0,5 | 0,10 | 0,05 | |
| 1 | 1,0000 | 6,3138 | 12,7062 |
| 2 | 0,8165 | 2,9200 | 4,3037 |
| 3 | 0,7649 | 2,3534 | 3,1824 |
| 4 | 0,7497 | 2,1318 | 2,7764 |
| 5 | 0,7267 | 2,0150 | 2,5706 |
| 6 | 0,7176 | 1,9432 | 2,4469 |
| 7 | 0,7111 | 1,8946 | 2,3646 |
| 8 | 0,7064 | 1,8595 | 2,3060 |
| 9 | 0,7027 | 1,8331 | 2,2622 |
| 10 | 0,6998 | 1,8125 | 2,2281 |
| 11 | 0,6974 | 1,7959 | 2,2010 |
| 12 | 0,6955 | 1,7823 | 2,1788 |
| 13 | 0,6938 | 1,7709 | 2,1604 |
| 14 | 0,6924 | 1,7613 | 2,1448 |
| 15 | 0,6912 | 1,7530 | 2,1314 |
| 16 | 0,6901 | 1,7459 | 2,1190 |
| 17 | 0,6892 | 1,7396 | 2,1098 |
| 18 | 0,6884 | 1,7341 | 2,1009 |
| 19 | 0,6876 | 1,7291 | 2,0930 |
| 20 | 0,6870 | 1,7247 | 2,0860 |
| 21 | 0,6864 | 1,7207 | 2,0796 |
| 22 | 0,6858 | 1,7171 | 2,0739 |
| 23 | 0,6853 | 1,7139 | 2,0687 |
| 24 | 0,6848 | 1,7109 | 2,0639 |
| 25 | 0,6844 | 1,7081 | 2,0595 |
| 26 | 0,6840 | 1,7056 | 2,0555 |
| 27 | 0,6837 | 1,7033 | 2,0518 |
| 28 | 0,6834 | 1,7011 | 2,0484 |
| 29 | 0,6830 | 1,6991 | 2,0452 |
| 30 | 0,6828 | 1,6973 | 2,0423 |
| 40 | 0,6807 | 1,6839 | 2,0211 |
| 60 | 0,6786 | 1,6706 | 2,0003 |
| 120 | 0,6765 | 1,6577 | 1,9840 |
| ∞ | 0,6750 | 1,6479 | 1,9647 |
| – | 0,25 | 0,05 | 0,025 |
| Уровень значимости α(односторонняя критическая область) | |||
Таблица 8
Значения функции Лапласа
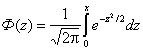
| Х | Ф(x) | х | Ф(х) | Х | Ф(х) | х | Ф(х) |
| 0,00 | 0,0000 | 0,38 | 0,1480 | 0,75 | 0,2734 | 1,12 | 0,3686 |
| 0,01 | 0,0040 | 0,39 | 0,1517 | 0,76 | 0,2764 | 1,13 | 0,3708 |
| 0,02 | 0,0080 | 0,40 | 0,1554 | 0,77 | 0,2794 | 1,14 | 0,3729 |
| 0,03 | 0,0120 | 0,41 | 0,1591 | 0,78 | 0,2823 | 1,15 | 0,3749 |
| 0,04 | 0,0160 | 0,42 | 0,1628 | 0,79 | 0,2852 | 1,16 | 0,3770 |
| 0,05 | 0,0199 | 0,43 | 0,1664 | 0,80 | 0,2881 | 1,17 | 0,3790 |
| 0,06 | 0,0239 | 0,44 | 0,1700 | 0,81 | 0,2910 | 1,18 | 0,3810 |
| 0,07 | 0,0279 | 0,45 | 0,1736 | 0,82 | 0,2939 | 1,20 | 0,3849 |
| 0,08 | 0,0319 | 0,46 | 0,1772 | 0,83 | 0,2967 | 1,21 | 0,3869 |
| 0,09 | 0,0359 | 0,47 | 0,1808 | 0,84 | 0,2995 | 1,22 | 0,3883 |
| 0,10 | 0,0398 | 0,48 | 0,1844 | 0,85 | 0,3023 | 1,23 | 0,3907 |
| 0,12 | 0,0478 | 0,49 | 0,1879 | 0,86 | 0,3051 | 1,24 | 0,3925 |
| 0,13 | 0,0517 | 0,50 | 0,1915 | 0,87 | 0,3078 | 1,25 | 0,3944 |
| 0,14 | 0,0557 | 0,51 | 0,1950 | 0,88 | 0,3106 | 1,26 | 0,3962 |
| 0,15 | 0,0596 | 0,52 | 0,1985 | 0,89 | 0,3133 | 1,27 | 0,3980 |
| 0,16 | 0,0636 | 0,53 | 0,2019 | 0,90 | 0,3159 | 1,28 | 0,3997 |
| 0,17 | 0,0675 | 0,54 | 0,2054 | 0,91 | 0,3186 | 1,29 | 0,4015 |
| 0,18 | 0,0714 | 0,55 | 0,2088 | 0,92 | 0,3212 | 1,30 | 0,4032 |
| 0,19 | 0,0753 | 0,56 | 0,2123 | 0,93 | 0,3238 | 1,31 | 0,4049 |
| 0,20 | 0,0793 | 0,57 | 0,2157 | 0,94 | 0,3264 | 1,32 | 0,4066 |
| 0,21 | 0,0832 | 0,58 | 0,2190 | 0,95 | 0,3289 | 1,33 | 0,4082 |
| 0,22 | 0,0871 | 0,59 | 0,2224 | 0,96 | 0,3315 | 1,34 | 0,4099 |
| 0,23 | 0,0910 | 0,60 | 0,2267 | 0,97 | 0,3340 | 1,35 | 0,4115 |
| 0,24 | 0,0948 | 0,61 | 0,2291 | 0,98 | 0,3365 | 1,36 | 0,4131 |
| 0,25 | 0,0987 | 0,62 | 0,2324 | 0,99 | 0,3389 | 1,37 | 0,4147 |
| 0,26 | 0,1026 | 0,63 | 0,2357 | 1,00 | 0,3413 | 1,38 | 0,4162 |
| 0,27 | 0,1064 | 0,64 | 0,2389 | 1,01 | 0,3438 | 1,39 | 0,4177 |
| 0,28 | 0,1103 | 0,65 | 0,2422 | 1,02 | 0,3461 | 1,40 | 0,4192 |
| 0,29 | 0,1141 | 0,66 | 0,2454 | 1,03 | 0,3485 | 1,41 | 0,4207 |
| 0,30 | 0,1179 | 0,67 | 0,2486 | 1,04 | 0,3508 | 1,42 | 0,4222 |
| 0,31 | 0,1217 | 0,68 | 0,2517 | 1,05 | 0,3531 | 1,43 | 0,4230 |
| 0,32 | 0,1255 | 0,69 | 0,2549 | 1,06 | 0,3554 | 1,44 | 0,4251 |
| 0,33 | 0,1293 | 0,70 | 0,2580 | 1,07 | 0,3577 | 1,45 | 0,4265 |
| 0,34 | 0,1331 | 0,71 | 0,2611 | 1,08 | 0,3599 | 1,46 | 0,4279 |
| 0,35 | 0,1368 | 0,72 | 0,2642 | 1,09 | 0,3621 | 1,47 | 0,4292 |
| 0,36 | 0,1406 | 0,73 | 0,2673 | 1,10 | 0,3643 | 1,48 | 0,4306 |
| 0,37 | 0,1443 | 0,74 | 0,2703 | 1,11 | 0,3665 | 1,49 | 0,4319 |
| Х | Ф(х) | х | Ф(х) | х | Ф(х) | х | Ф(х) |
| 1,50 | 0,4332 | 1,90 | 0,4713 | 2,30 | 0,4893 | 2,81 | 0,4975 |
| 1,51 | 0,4345 | 1,91 | 0,4719 | 2,31 | 0,4896 | 2,82 | 0,4976 |
| 1,52 | 0,4357 | 1,92 | 0,4726 | 2,32 | 0,4898 | 2,83 | 0,4977 |
| 1,53 | 0,4370 | 1,93 | 0,4732 | 2,33 | 0,4901 | 2,84 | 0,4978 |
| 1,54 | 0,4382 | 1,94 | 0,4738 | 2,34 | 0,4904 | 2,85 | 0,49781 |
| 1,55 | 0,4394 | 1,95 | 0,4744 | 2,35 | 0,4906 | 2,86 | 0,49782 |
| 1,56 | 0,4406 | 1,96 | 0,4750 | 2,36 | 0,4909 | 2,87 | 0,49795 |
| 1,57 | 0,4418 | 1,97 | 0,4756 | 2,37 | 0,4911 | 2,88 | 0,49801 |
| 1,58 | 0,4429 | 1,98 | 0,4761 | 2,38 | 0,4913 | 2,89 | 0,49807 |
| 1,59 | 0,4441 | 1,99 | 0,4767 | 2,39 | 0,4915 | 2,90 | 0,49813 |
| 1,60 | 0,4452 | 2,00 | 0,4772 | 2,40 | 0,4918 | 2,91 | 0,49819 |
| 1,61 | 0,4463 | 2,01 | 0,4773 | 2,41 | 0,4920 | 2,92 | 0,49820 |
| 1,62 | 0,4474 | 2,02 | 0,4783 | 2,42 | 0,4922 | 2,93 | 0,49830 |
| 1,63 | 0,4484 | 2,03 | 0,4788 | 2,43 | 0,4924 | 2,94 | 0,49840 |
| 1,64 | 0,4495 | 2,04 | 0,4793 | 2,44 | 0,4927 | 2,95 | 0,49841 |
| 1,65 | 0,4505 | 2,05 | 0,4798 | 2,45 | 0,4929 | 2,96 | 0,49846 |
| 1,66 | 0,4515 | 2,06 | 0,4803 | 2,46 | 0,4931 | 2,97 | 0,49851 |
| 1,67 | 0,4525 | 2,07 | 0,4808 | 2,47 | 0,4932 | 2,98 | 0,49860 |
| 1,68 | 0,4535 | 2,08 | 0,4812 | 2,48 | 0,4934 | 2,99 | 0,49861 |
| 1,69 | 0,4545 | 2,09 | 0,4817 | 2,49 | 0,4936 | 3,00 | 0,49865 |
| 1,70 | 0,4554 | 2,10 | 0,4821 | 2,50 | 0,4938 | 3,10 | 0,49903 |
| 1,71 | 0,4564 | 2,11 | 0,4826 | 2,51 | 0,4939 | 3,20 | 0,49931 |
| 1,72 | 0,4573 | 2,12 | 0,4830 | 2,52 | 0,4941 | 3,30 | 0,49951 |
| 1,73 | 0,4582 | 2,13 | 0,4834 | 2,53 | 0,4942 | 3,40 | 0,49966 |
| 1,74 | 0,4591 | 2,14 | 0,4838 | 2,54 | 0,4945 | 3,50 | 0,49976 |
| 1,75 | 0,4599 | 2,15 | 0,4843 | 2,55 | 0,4946 | 3,60 | 0,499841 |
| 1,76 | 0,4608 | 2,16 | 0,4846 | 2,60 | 0,4953 | 3,80 | 0,499928 |
| 1,77 | 0,4616 | 2,17 | 0,4850 | 2,67 | 0,4962 | 4,00 | 0,499968 |
| 1,78 | 0,4625 | 2,18 | 0,4854 | 2,68 | 0,4963 | 4,10 | 0,499979 |
| 1,79 | 0,4633 | 2,19 | 0,4858 | 2,69 | 0,4964 | 4,20 | 0,499987 |
| 1,80 | 0,4641 | 2,20 | 0,4861 | 2,70 | 0,4965 | 4,30 | 0,499991 |
| 1,81 | 0,4649 | 2,21 | 0,4864 | 2,71 | 0,4966 | 4,40 | 0,499995 |
| 1,82 | 0,4656 | 2,22 | 0,4868 | 2,72 | 0,4967 | 4,50 | 0,499997 |
| 1,83 | 0,4664 | 2,23 | 0,4872 | 2,73 | 0,4968 | 4,60 | 0,499997 |
| 1,84 | 0,4671 | 2,24 | 0,4875 | 2,74 | 0,4969 | 4,70 | 0,499997 |
| 1,85 | 0,4678 | 2,25 | 0,4878 | 2,75 | 0,4970 | 4,80 | 0,499997 |
| 1,86 | 0,4686 | 2,26 | 0,4881 | 2,76 | 0,4971 | 4,90 | 0,499997 |
| 1,87 | 0,4693 | 2,27 | 0,4884 | 2,77 | 0,4972 | 5,00 | 0,499997 |
| 1,88 | 0,4699 | 2,28 | 0,4887 | 2,78 | 0,4973 | – | – |
| 1,89 | 0,4706 | 2,29 | 0,4890 | 2,80 | 0,4974 | – | – |
Таблица 9
Критические точки распределения χ2
| Число степеней свободы k | Уровень значимости α | |||
| 0,20 | 0,10 | 0,05 | 0,025 | |
| 1 | 1,642 | 2,706 | 3,841 | 5,024 |
| 2 | 3,219 | 4,605 | 5,991 | 7,378 |
| 3 | 4,642 | 6,251 | 7,815 | 9,348 |
| 4 | 5,989 | 7,779 | 9,488 | 11,143 |
| 5 | 7,289 | 9,236 | 11,070 | 12,832 |
| 6 | 8,558 | 10,645 | 12,592 | 14,449 |
| 7 | 9,803 | 12,017 | 14,067 | 16,013 |
| 8 | 11,030 | 13,362 | 15,507 | 17,535 |
| 9 | 12,242 | 14,684 | 16,919 | 19,023 |
| 10 | 13,442 | 15,987 | 18,307 | 20,483 |
| 11 | 14,631 | 17,275 | 19,676 | 21,920 |
| 12 | 15,812 | 18,549 | 21,026 | 23,336 |
| 13 | 16,985 | 19,812 | 22,362 | 24,736 |
| 14 | 18,151 | 21,064 | 23,685 | 26,129 |
| 15 | 19,311 | 22,307 | 24,996 | 27,488 |
| 16 | 20,465 | 23,542 | 26,296 | 28,845 |
| 17 | 21,615 | 24,769 | 27,587 | 30,191 |
| 18 | 22,766 | 25,989 | 28,869 | 31,536 |
| 19 | 23,900 | 27,204 | 30,144 | 32,852 |
| 20 | 25,038 | 28,412 | 31,410 | 34,170 |
| 21 | 26,171 | 29,615 | 32,671 | 35,479 |
| 22 | 27,301 | 30,813 | 33,924 | 36,781 |
| 23 | 28,429 | 32,007 | 35,172 | 38,076 |
| 24 | 29,553 | 33,196 | 36,415 | 39,364 |
| 25 | 30,675 | 34,382 | 37,652 | 40,646 |
| 26 | 31,795 | 35,563 | 38,885 | 41,923 |
| 27 | 32,912 | 36,741 | 40,113 | 43,194 |
| 28 | 34,027 | 37,916 | 41,337 | 44,461 |
| 29 | 35,139 | 39,087 | 42,557 | 45,722 |
| 30 | 36,250 | 40,256 | 43,773 | 46,979 |
| 31 | 37,350 | 41,422 | 44,985 | 48,232 |
| 32 | 38,466 | 42,585 | 46,194 | 49,480 |
| 33 | 39,572 | 43,745 | 47,400 | 50,725 |
| 34 | 40,676 | 44,903 | 48,602 | 51,966 |
| 35 | 41,778 | 46,059 | 49,802 | 53,203 |
| 36 | 42,879 | 47,212 | 50,998 | 54,437 |
Таблица 10
Критические точки распределения Фишера. Уровень значимости
α = 0,05 (k1 – число степеней свободы большей дисперсии,
k2 – число степеней свободы меньшей дисперсии)
| k2 | k1 = 1 | k1 = 2 | k1 = 3 | k1 = 4 | k1 = 5 | k1 = 6 | k1 = 7 | k1 = 8 | k1 = 9 |
| 1 | 161,45 | 199,50 | 215,71 | 224,58 | 230,16 | 233,99 | 236,77 | 238,88 | 240,54 |
| 2 | 18,513 | 19,000 | 19,164 | 19,247 | 19,296 | 19,330 | 19,353 | 19,371 | 18,385 |
| 3 | 10,128 | 9,5521 | 9,2766 | 9,1172 | 9,0135 | 8,9406 | 8,8868 | 8,8452 | 8,8123 |
| 4 | 7,7086 | 6,9443 | 6,3914 | 6,3883 | 6,2560 | 6,1631 | 6,0942 | 6,0410 | 5,9988 |
| 5 | 6,6079 | 5,7861 | 5,4095 | 5,1922 | 5,0503 | 4,9503 | 4,8759 | 4,8183 | 4,7725 |
| 6 | 5,9874 | 5,1433 | 4,7571 | 4,5337 | 4,3874 | 4,2839 | 4,2066 | 4,1468 | 4,0990 |
| 7 | 5,5914 | 4,7374 | 4,3468 | 4,1203 | 3,9715 | 3,8660 | 3,7870 | 3,7257 | 3,6767 |
| 8 | 5,3177 | 4,4590 | 4,0662 | 3,8378 | 3,6875 | 3,5806 | 3,5005 | 3,4381 | 3,3881 |
| 9 | 5,1174 | 4,2565 | 3,8626 | 3,6331 | 3,4817 | 3,3738 | 3,2927 | 3,2296 | 3,1789 |
| 10 | 4,9646 | 4,1028 | 3,7083 | 3,4780 | 3,3258 | 3,2172 | 3,1355 | 3,0717 | 3,0204 |
| 11 | 4,8443 | 3,9823 | 3,5874 | 3,3567 | 3,2039 | 3,0946 | 3,0123 | 2,9480 | 2,8962 |
| 12 | 4,7472 | 3,8853 | 3,4903 | 3,2592 | 3,1059 | 2,9961 | 2,9134 | 2,8486 | 2,7964 |
| 13 | 4,6672 | 3,8056 | 3,4105 | 3,1791 | 3,0254 | 2,9153 | 2,8321 | 2,7669 | 2,7144 |
| 14 | 4,6001 | 3,7289 | 3,3439 | 3,1122 | 2,9582 | 2,8477 | 2,7642 | 2,6987 | 2,6458 |
| 15 | 4,5431 | 3,6823 | 3,2874 | 3,0556 | 2,9013 | 2,7905 | 2,7066 | 2,6408 | 2,5876 |
| 16 | 4,4940 | 3,6337 | 3,2389 | 3,0069 | 2,8524 | 2,7413 | 2,6572 | 2,5911 | 2,5377 |
| 17 | 4,4513 | 3,5913 | 3,1968 | 2,9647 | 2,8100 | 2,6987 | 2,6143 | 2,5480 | 2,4943 |
| 18 | 4,4139 | 3,5546 | 3,1599 | 2,9277 | 2,7729 | 2,6613 | 2,5767 | 2,5102 | 2,4563 |
| 19 | 4,3808 | 3,5219 | 3,1274 | 2,8951 | 2,7401 | 2,6283 | 2,5435 | 2,4768 | 2,4227 |
| 20 | 4,3513 | 3,4928 | 3,0984 | 2,8661 | 2,7109 | 2,5990 | 2,5140 | 2,4471 | 2,3928 |
| 21 | 4,3248 | 3,4668 | 3,0725 | 2,8401 | 2,6848 | 2,5727 | 2,4876 | 2,4205 | 2,3661 |
| 22 | 4,3009 | 3,4434 | 3,0491 | 2,8167 | 2,6613 | 2,5491 | 2,4638 | 2,3965 | 2,3419 |
| 23 | 4,2793 | 3,4221 | 3,0280 | 2,7955 | 2,6400 | 2,5277 | 2,4422 | 2,3748 | 2,3201 |
| 24 | 4,2597 | 3,4028 | 3,0088 | 2,7763 | 2,6207 | 2,5082 | 2,4226 | 2,3551 | 2,3002 |
| 25 | 4,2417 | 3,3852 | 2,9912 | 2,7587 | 2,6030 | 2,4904 | 2,4047 | 2,3371 | 2,2821 |
| 26 | 4,2252 | 3,3690 | 2,9751 | 2,7426 | 2,5868 | 2,4741 | 2,3883 | 2,3205 | 2,2655 |
| 27 | 4,2100 | 3,3541 | 2,9604 | 2,7278 | 2,5719 | 2,4591 | 2,3732 | 2,3053 | 2,2501 |
| 28 | 4,1960 | 3,3404 | 2,9467 | 2,7141 | 2,5581 | 2,4453 | 2,3593 | 2,2913 | 2,2360 |
| 29 | 4,1830 | 3,3277 | 2,9340 | 2,7014 | 2,5454 | 2,4324 | 2,3463 | 2,2782 | 2,2239 |
| 30 | 4,1709 | 3,3158 | 2,9223 | 2,6896 | 2,5336 | 2,4205 | 2,3343 | 2,2662 | 2,2107 |
| 40 | 4,0848 | 3,2317 | 2,8387 | 2,6060 | 2,4459 | 2,3359 | 2,2490 | 2,1802 | 2,1240 |
| 60 | 4,0012 | 3,1904 | 2,7581 | 2,5252 | 2,3683 | 2,2540 | 2,1665 | 2,0970 | 2,0401 |
| 120 | 3,9201 | 3,0718 | 2,6802 | 2,4472 | 2,2900 | 2,1750 | 2,0868 | 2,0164 | 1,9588 |
| ∞ | 3,8415 | 2,9957 | 2,6049 | 2,3719 | 2,2141 | 2,0986 | 2,0096 | 1,9384 | 1,8799 |
| k2 | k1 = 10 | k1 = 12 | k1 = 15 | k1 = 20 | k1 = 30 | k1= 40 | k1 = 60 | k1 = 120 | k1 = ∞ |
| 1 | 241,88 | 243,91 | 245,95 | 248,01 | 250,09 | 251,14 | 252,20 | 253,25 | 254,32 |
| 2 | 19,396 | 19,413 | 19,429 | 19,446 | 19,462 | 19,471 | 19,479 | 19,487 | 19,496 |
| 3 | 8,7855 | 8,7446 | 8,7029 | 8,6602 | 8,6166 | 8,5944 | 8,5720 | 8,5484 | 8,5265 |
| 4 | 5,9644 | 5,9117 | 5,8578 | 5,8025 | 5,7459 | 5,7170 | 5,6878 | 5,6581 | 5,6281 |
| 5 | 4,7351 | 4,6777 | 4,6188 | 4,5581 | 4,4957 | 4,4638 | 4,4314 | 4,3984 | 4,3650 |
| 6 | 4,0600 | 3,9999 | 3,9381 | 3,8742 | 3,8082 | 3,7743 | 3,7398 | 3,7047 | 3,6688 |
| 7 | 3,6365 | 3,5747 | 3,5108 | 3,4445 | 3,3758 | 3,3404 | 3,3043 | 3,2674 | 3,2298 |
| 8 | 3,3472 | 3,2540 | 3,2184 | 3,1503 | 3,0794 | 3,0428 | 3,0053 | 2,9669 | 2,9276 |
| 9 | 3,1373 | 3,0729 | 3,0061 | 2,9365 | 2,8637 | 2,8259 | 2,7872 | 2,7445 | 2,7067 |
| 10 | 2,9783 | 2,9130 | 2,8450 | 2,7740 | 2,6996 | 2,6609 | 2,6211 | 2,5801 | 2,5379 |
| 11 | 2,8536 | 2,7876 | 2,7186 | 2,6464 | 2,5705 | 2,5309 | 2,4901 | 2,4480 | 2,4045 |
| 12 | 2,7534 | 2,6866 | 2,6169 | 2,5436 | 2,4663 | 2,4259 | 2,3842 | 2,3410 | 2,2962 |
| 13 | 2,6710 | 2,6037 | 2,5331 | 2,4589 | 2,3803 | 2,3392 | 2,2966 | 2,2524 | 2,2064 |
| 14 | 2,6021 | 2,5342 | 2,4630 | 2,3879 | 2,3082 | 2,2664 | 2,2230 | 2,1778 | 2,1307 |
| 15 | 2,5437 | 2,4753 | 2,4035 | 2,3275 | 2,2468 | 2,2043 | 2,1601 | 2,1141 | 2,0658 |
| 16 | 2,4935 | 2,4247 | 2,3522 | 2,2756 | 2,1938 | 2,1507 | 2,1058 | 2,0589 | 2,0096 |
| 17 | 2,4499 | 2,3807 | 2,3077 | 2,2304 | 2,1477 | 2,1040 | 2,0584 | 2,0107 | 1,9604 |
| 18 | 2,4117 | 2,3421 | 2,2686 | 2,1906 | 2,1071 | 2,0629 | 2,0166 | 1,9681 | 1,9168 |
| 19 | 2,3779 | 2,3080 | 2,2341 | 2,1555 | 2,0712 | 2,0264 | 1,9796 | 1,9302 | 1,8780 |
| 20 | 2,3479 | 2,2776 | 2,2033 | 2,1342 | 2,0391 | 1,9938 | 1,9464 | 1,8963 | 1,8432 |
| 21 | 2,3210 | 2,2504 | 2,1757 | 2,0960 | 2,0102 | 1,9645 | 1,9163 | 1,8657 | 1,8117 |
| 22 | 2,2967 | 2,2258 | 2,1508 | 2,0707 | 1,9842 | 1,9380 | 1,8895 | 1,8380 | 1,7831 |
| 23 | 2,2747 | 2,2036 | 2,1282 | 2,0476 | 1,9605 | 1,9139 | 1,8649 | 1,8128 | 1,7570 |
| 24 | 2,2547 | 2,1834 | 2,1077 | 2,0267 | 1,9390 | 1,8920 | 1,8424 | 1,7897 | 1,7331 |
| 25 | 2,2365 | 2,1649 | 2,0889 | 2,0075 | 1,9193 | 1,8718 | 1,8217 | 1,7684 | 1,7110 |
| 26 | 2,2197 | 2,1479 | 2,0716 | 1,9898 | 1,9010 | 1,8533 | 1,8027 | 1,7488 | 1,6906 |
| 27 | 2,2043 | 2,1323 | 2,0558 | 1,9736 | 1,8842 | 1,8361 | 1,7851 | 1,7307 | 1,6717 |
| 28 | 2,1900 | 2,1179 | 2,0411 | 1,9586 | 1,8687 | 1,8263 | 1,7689 | 1,7118 | 1,6541 |
| 29 | 2,1768 | 2,1045 | 2,0275 | 1,9446 | 1,8543 | 1,8055 | 1,7537 | 1,6981 | 1,6377 |
| 30 | 2,1646 | 2,0921 | 2,0148 | 1,9317 | 1,8409 | 1,7918 | 1,7396 | 1,6815 | 1,6223 |
| 40 | 2,0772 | 2,0035 | 1,9245 | 1,8389 | 1,7444 | 1,6928 | 1,6373 | 1,5766 | 1,5089 |
| 60 | 1,9926 | 1,9174 | 1,8364 | 1,7486 | 1,6491 | 1,5943 | 1,5343 | 1,4673 | 1,3893 |
| 120 | 1,9105 | 1,8337 | 1,7505 | 1,6587 | 1,5543 | 1,4952 | 1,4290 | 1,3519 | 1,2539 |
| ∞ | 1,8307 | 1,7522 | 1,6664 | 1,5705 | 1,4591 | 1,3940 | 1,3180 | 1,2214 | 1,0000 |
| k2 | k1= 1 | k1 = 2 | k1 = 3 | k1 = 4 | k1 = 5 | k1 = 6 | k1 = 7 | k1 = 8 | k1 = 9 |
| 1 | 39,864 | 49,500 | 53,593 | 55,833 | 57,241 | 58,204 | 58,906 | 59,439 | 59,858 |
| 2 | 8,5263 | 9,0000 | 9,1618 | 9,2434 | 9,2926 | 9,3255 | 9,3491 | 9,3668 | 9,3805 |
| 3 | 5,5383 | 5,4624 | 5,3908 | 5,3427 | 5,3092 | 5,2847 | 5,2662 | 5,2517 | 5,2400 |
| 4 | 4,5448 | 4,3246 | 4,1908 | 4,1073 | 4,0506 | 4,0098 | 3,9790 | 3,9549 | 3,9357 |
| 5 | 4,0604 | 3,7797 | 3,6195 | 3,5202 | 3,4530 | 3,4045 | 3,3679 | 3,3393 | 3,3163 |
| 6 | 3,7760 | 3,4633 | 3,2888 | 3,1808 | 3,1075 | 3,0546 | 3,0145 | 2,9830 | 2,9577 |
| 7 | 3,5894 | 3,2574 | 3,0741 | 2,9605 | 2,8833 | 2,8274 | 2,7849 | 2,7516 | 2,7247 |
| 8 | 3,4579 | 3,1131 | 2,9238 | 2,8064 | 2,7265 | 2,6683 | 2,6241 | 2,5893 | 2,5612 |
| 9 | 3,3603 | 3,0065 | 2,8129 | 2,6927 | 2,6106 | 2,5509 | 2,5053 | 2,4694 | 2,4403 |
| 10 | 3,2850 | 2,9245 | 2,7277 | 2,6053 | 2,5216 | 2,4606 | 2,4140 | 2,3772 | 2,3473 |
| 11 | 3,2252 | 2,8595 | 2,6602 | 2,5362 | 2,4512 | 2,3891 | 2,3416 | 2,3040 | 2,2735 |
| 12 | 3,1765 | 2,8068 | 2,6055 | 2,4801 | 2,3940 | 2,3310 | 2,2828 | 2,2446 | 2,2135 |
| 13 | 3,1362 | 2,7632 | 2,5603 | 2,4337 | 2,3467 | 2,2830 | 2,2341 | 2,1953 | 2,1638 |
| 14 | 3,1022 | 2,7265 | 2,5222 | 2,3947 | 2,3069 | 2,2426 | 2,1931 | 2,1539 | 2,1220 |
| 15 | 3,0732 | 2,6952 | 2,4898 | 2,3614 | 2,2730 | 2,2081 | 2,1582 | 2,1185 | 2,0862 |
| 16 | 3,0481 | 2,6682 | 2,4618 | 2,3327 | 2,2438 | 2,1783 | 2,1280 | 2,0880 | 2,0553 |
| 17 | 3,0262 | 2,6446 | 2,4374 | 2,3077 | 2,2181 | 2,1524 | 2,1017 | 2,0613 | 2,0284 |
| 18 | 3,0070 | 2,6239 | 2,4160 | 2,2858 | 2,1958 | 2,1296 | 2,0785 | 2,0379 | 2,0047 |
| 19 | 2,9899 | 2,6056 | 2,3970 | 2,2663 | 2,1760 | 2,1094 | 2,0580 | 2,0171 | 1,9836 |
| 20 | 2,9747 | 2,5893 | 2,3801 | 2,2489 | 2,1582 | 2,0913 | 2,0397 | 1,9985 | 1,9649 |
| 21 | 2,9609 | 2,5746 | 2,3649 | 2,2333 | 2,1423 | 2,0751 | 2,0232 | 1,9819 | 1,9480 |
| 22 | 2,9486 | 2,5613 | 2,3512 | 2,2193 | 2,1279 | 2,0605 | 2,0084 | 1,9668 | 1,9327 |
| 23 | 2,9374 | 2,5493 | 2,3387 | 2,2065 | 2,1149 | 2,0472 | 1,9949 | 1,9531 | 1,9189 |
| 24 | 2,9271 | 2,5383 | 2,3274 | 2,1949 | 2,1030 | 2,0351 | 1,9826 | 1,9407 | 1,9063 |
| 25 | 2,9177 | 2,5283 | 2,3170 | 2,1843 | 2,0922 | 2,0241 | 1,9714 | 1,9292 | 1,8947 |
| 26 | 2,9091 | 2,5191 | 2,3075 | 2,1745 | 2,0822 | 2,0139 | 1,9610 | 1,9188 | 1,8841 |
| 27 | 2,9012 | 2,5106 | 2,2987 | 2,1655 | 2,0730 | 2,0045 | 1,9515 | 1,9091 | 1,8743 |
| 28 | 2,8939 | 2,5028 | 2,2906 | 2,1571 | 2,0645 | 1,9959 | 1,9427 | 1,9001 | 1,8652 |
| 29 | 2,8871 | 2,4955 | 2,2831 | 2,1494 | 2,0566 | 1,9878 | 1,9345 | 1,8918 | 1,8568 |
| 30 | 2,8807 | 2,4887 | 2,2761 | 2,1423 | 2,0492 | 1,9803 | 1,9269 | 1,8841 | 1,8490 |
| 40 | 2,8354 | 2,4404 | 2,2261 | 2,0909 | 1,9968 | 1,9269 | 1,8725 | 1,8289 | 1,7929 |
| 60 | 2,7914 | 2,3933 | 2,1774 | 2,0410 | 1,9457 | 1,8747 | 1,8194 | 1,7748 | 1,7380 |
| 120 | 2,7478 | 2,3473 | 2,1300 | 1,9923 | 1,8959 | 1,8238 | 1,7675 | 1,7220 | 1,6843 |
| ∞ | 2,7055 | 2,3026 | 2,0838 | 1,9449 | 1,8473 | 1,7741 | 1,7167 | 1,6702 | 1,6315 |
| k2 | k1 = 10 | k1 = 12 | k1 = 15 | k1 = 20 | k1 = 30 | k1 = 40 | k1 = 60 | k1= 120 | k1 = ∞ |
| 1 | 60,195 | 60,705 | 61,220 | 61,740 | 62,265 | 63,529 | 62,794 | 63,061 | 63,328 |
| 2 | 9,3916 | 9,4081 | 9,4247 | 9,4413 | 9,4579 | 9,4663 | 9,4746 | 9,4829 | 9,4913 |
| 3 | 5,2304 | 5,2156 | 5,2003 | 5,1845 | 5,1681 | 5,1597 | 5,1512 | 5,1425 | 5,1337 |
| 4 | 3,9199 | 3,8955 | 3,8703 | 3,8413 | 3,8174 | 3,8036 | 3,7896 | 3,7753 | 3,7007 |
| 5 | 3,2974 | 3,2682 | 3,2380 | 3,2067 | 3,1741 | 3,1573 | 3,1402 | 3,1228 | 3,1050 |
| 6 | 2,9369 | 2,9047 | 2,8712 | 2,8363 | 2,8000 | 2,7812 | 2,7620 | 2,7423 | 2,7222 |
| 7 | 2,7025 | 2,6681 | 2,6322 | 2,5947 | 2,5555 | 2,5351 | 2,5142 | 2,4928 | 2,4708 |
| 8 | 2,5380 | 2,5020 | 2,4642 | 2,4246 | 2,3830 | 2,3614 | 2,3391 | 2,3162 | 2,2926 |
| 9 | 2,4163 | 2,3789 | 2,3396 | 2,2983 | 2,2547 | 2,2320 | 2,2085 | 2,1843 | 2,1592 |
| 10 | 2,3226 | 2,2841 | 2,2435 | 2,2007 | 2,1554 | 2,1317 | 2,1072 | 2,0819 | 2,0554 |
| 11 | 2,2482 | 2,2087 | 2,1671 | 2,1230 | 2,0762 | 2,0516 | 2,0261 | 1,9997 | 1,9721 |
| 12 | 2,1878 | 2,1474 | 2,1049 | 2,0597 | 2,0115 | 1,9861 | 1,9597 | 1,9323 | 1,9036 |
| 13 | 2,1376 | 2,0966 | 2,0532 | 2,0070 | 1,9576 | 1,9315 | 1,9043 | 1,8759 | 1,8462 |
| 14 | 2,0954 | 2,0537 | 2,0095 | 1,9525 | 1,9119 | 1,8852 | 1,8572 | 1,8280 | 1,7973 |
| 15 | 2,0593 | 2,0171 | 1,9722 | 1,9243 | 1,8728 | 1,8454 | 1,8168 | 1,7867 | 1,7551 |
| 16 | 2,0281 | 1,9854 | 1,9399 | 1,8913 | 1,8388 | 1,8108 | 1,7816 | 1,7507 | 1,7182 |
| 17 | 2,0009 | 1,9577 | 1,9117 | 1,8624 | 1,8090 | 1,7805 | 1,7506 | 1,7141 | 1,6856 |
| 18 | 1,9770 | 1,9333 | 1,8888 | 1,8368 | 1,7827 | 1,7537 | 1,7232 | 1,6910 | 1,6567 |
| 19 | 1,9557 | 1,9117 | 1,8647 | 1,8142 | 1,7592 | 1,7298 | 1,6988 | 1,6659 | 1,6308 |
| 20 | 1,9367 | 1,8924 | 1,8449 | 1,7938 | 1,7382 | 1,7083 | 1,6768 | 1,6433 | 1,6074 |
| 21 | 1,9197 | 1,8750 | 1,8272 | 1,7756 | 1,7193 | 1,6890 | 1,6569 | 1,6228 | 1,5862 |
| 22 | 1,9043 | 1,8593 | 1,8111 | 1,7590 | 1,7021 | 1,6714 | 1,6389 | 1,6042 | 1,5668 |
| 23 | 1,8903 | 1,8450 | 1,7964 | 1,7439 | 1,6864 | 1,6554 | 1,6224 | 1,5871 | 1,5490 |
| 24 | 1,8775 | 1,8319 | 1,7831 | 1,7302 | 1,6721 | 1,6407 | 1,6073 | 1,5715 | 1,5327 |
| 25 | 1,8658 | 1,8300 | 1,7708 | 1,7175 | 1,6589 | 1,6272 | 1,5934 | 1,5570 | 1,5176 |
| 26 | 1,8550 | 1,8090 | 1,7598 | 1,7059 | 1,6468 | 1,6147 | 1,5805 | 1,5437 | 1,5036 |
| 27 | 1,8432 | 1,7989 | 1,7492 | 1,6951 | 1,6356 | 1,6032 | 1,5686 | 1,5313 | 1,4906 |
| 28 | 1,8359 | 1,7895 | 1,7395 | 1,6832 | 1,6252 | 1,5925 | 1,5575 | 1,5198 | 1,4784 |
| 29 | 1,8274 | 1,7808 | 1,7306 | 1,0759 | 1,6155 | 1,5825 | 1,5472 | 1,5090 | 1,4670 |
| 30 | 1,8195 | 1,7727 | 1,7223 | 1,6673 | 1,6065 | 1,5732 | 1,5376 | 1,4989 | 1,4564 |
| 40 | 1,7627 | 1,7146 | 1,6624 | 1,6052 | 1,5411 | 1,5056 | 1,4672 | 1,4248 | 1,3769 |
| 60 | 1,7070 | 1,6574 | 1,6034 | 1,5435 | 1,4755 | 1,4373 | 1,3952 | 1,3476 | 1,2915 |
| 120 | 1,6524 | 1,6012 | 1,5450 | 1,4821 | 1,4094 | 1,3676 | 1,3203 | 1,2646 | 1,1926 |
| ∞ | 1,5987 | 1,5458 | 1,4871 | 1,4206 | 1,3419 | 1,2951 | 1,2400 | 1,1686 | 1,0000 |
Критерий Кокрена. Верхние пятипроцентные (α = 0,05)
Таблица 11
критические значения для статистики 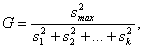 построенной по k независимым оценкам дисперсий, каждая из которых обладает f степенями свободы
построенной по k независимым оценкам дисперсий, каждая из которых обладает f степенями свободы
| k | f= 1 | f = 2 | f = 3 | f = 4 | f = 5 | f = 6 | f = 7 |
| 2 | 0,9985 | 0,9750 | 0,9792 | 0,9057 | 0,8772 | 0,8534 | 0, 8332 |
| 3 | 0,9669 | 0,8709 | 0,7977 | 0,7457 | 0,7071 | 0,6771 | 0, 6530 |
| 4 | 0,9065 | 0,7679 | 0,6841 | 0,6287 | 0,5895 | 0,5598 | 0, 5365 |
| 5 | 0,8412 | 0,6838 | 0,5981 | 0,5440 | 0,5063 | 0,4783 | 0, 4564 |
| 6 | 0,7808 | 0,6161 | 0,5321 | 0,4809 | 0,4447 | 0,4184 | 0, 3980 |
| 7 | 0,7271 | 0,5612 | 0,4800 | 0,4307 | 0,3974 | 0,3726 | 0, 3535 |
| 8 | 0,6798 | 0,5157 | 0,4377 | 0,3910 | 0,3595 | 0,3362 | 0, 3185 |
| 9 | 0,6385 | 0,4775 | 0,4027 | 0,3584 | 0,3286 | 0,3067 | 0, 2910 |
| 10 | 0,6020 | 0,4450 | 0,3733 | 0,3311 | 0,3029 | 0,2823 | 0, 2666 |
| 12 | 0,5410 | 0,3924 | 0,3264 | 0,2880 | 0,2624 | 0,2439 | 0, 2299 |
| 15 | 0,4709 | 0,3346 | 0,2758 | 0,2419 | 0,2195 | 0,2034 | 0, 1911 |
| 20 | 0,3894 | 0,2705 | 0,2205 | 0,1921 | 0,1735 | 0,1602 | 0, 1501 |
| 24 | 0,3434 | 0,2354 | 0,1907 | 0,1656 | 0,1493 | 0,1374 | 0, 1286 |
| 30 | 0,2929 | 0,1980 | 0,1593 | 0,1377 | 0,1237 | 0,1137 | 0, 1051 |
| 40 | 0,2370 | 0,1576 | 0,1259 | 0,1082 | 0,0968 | 0,0887 | 0, 0827 |
| 60 | 0,1737 | 0,1131 | 0,0895 | 0,0765 | 0,0682 | 0,0623 | 0, 0583 |
| 120 | 0,0998 | 0,0632 | 0,0495 | 0,0419 | 0,0371 | 0,0337 | 0, 0312 |
| ∞ | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
| k | f = 8 | f = 9 | f = 10 | f = 16 | f = 36 | f = 144 | f = ∞ |
| 2 | 0,8159 | 0,8010 | 0,7880 | 0,7341 | 0,6602 | 0,5813 | 0,5000 |
| 3 | 0,6333 | 0,6167 | 0,6025 | 0,5466 | 0,4748 | 0,4031 | 0,3333 |
| 4 | 0,5175 | 0,5017 | 0,4884 | 0,4366 | 0,3720 | 0,3093 | 0,2500 |
| 5 | 0,4387 | 0,4241 | 0,4118 | 0,3645 | 0,3066 | 0,2513 | 0,2000 |
| 6 | 0,3817 | 0,3682 | 0,3568 | 0,3135 | 0,2612 | 0,2119 | 0,1667 |
| 7 | 0,3384 | 0,3259 | 0,3154 | 0,2756 | 0,2278 | 0,1833 | 0,1429 |
| 8 | 0,3043 | 0,2926 | 0,2829 | 0,2462 | 0,2022 | 0,1616 | 0,1250 |
| 9 | 0,2768 | 0,2659 | 0,2568 | 0,2226 | 0,1820 | 0,1446 | 0,1111 |
| 10 | 0,2541 | 0,2439 | 0,2353 | 0,2032 | 0,1635 | 0,1308 | 0,1000 |
| 12 | 0,2187 | 0,2098 | 0,2020 | 0,1737 | 0,1403 | 0,1100 | 0,0833 |
| 15 | 0,1815 | 0,1736 | 0,1671 | 0,1429 | 0,1144 | 0,0889 | 0,0667 |
| 20 | 0,1422 | 0,1357 | 0,1303 | 0,1108 | 0,0879 | 0,0675 | 0,0500 |
| 24 | 0,1216 | 0,1160 | 0,1113 | 0,0942 | 0,0743 | 0,0567 | 0,0417 |
| 30 | 0,1002 | 0,0958 | 0,0921 | 0,0771 | 0,0604 | 0,0457 | 0,0333 |
| 40 | 0,0780 | 0,0745 | 0,0713 | 0,0595 | 0,0462 | 0,0347 | 0,0250 |
| 60 | 0,0552 | 0,0520 | 0,0497 | 0,0411 | 0,0316 | 0,0234 | 0,0167 |
| 120 | 0,0292 | 0,0279 | 0,0266 | 0,0218 | 0,0165 | 0,0120 | 0,8300 |
| ∞ | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 | 0,0000 |
Таблица 12
Критерий Бартлетта. Процентные точки М-статистики, α = 0,05
| k | C1=0,0 | C1=0,5 | C1=1,0 | C1=1,5 | C1=2,0 | C1=2,5 | C1=3,0 | C1=3,5 | C1=4,0 |
| 3(a) | 5,99 | 6,47 | 6,89 | 7,80 | 7,38 | 7,39 | 7,22 | – | – |
| (b) | 5,99 | 6,22 | 6,43 | 6,64 | 6,84 | 7,03 | 7,22 | – | – |
| 4(a) | 7,81 | 8,24 | 8,63 | 8,96 | 9,21 | 9,38 | 9,43 | 9,37 | 9,18 |
| (b) | 7,81 | 8,00 | 8,17 | 8,35 | 8,52 | 8,69 | 8,85 | 9,02 | 9,18 |
| 5(a) | 9,49 | 9,88 | 10,24 | 10,57 | 10,86 | 11,08 | 11,24 | 11,32 | 11,31 |
| (b) | 9,49 | 9,65 | 9,80 | 9,96 | 10,11 | 10,27 | 10,42 | 10,57 | 10,72 |
| 6(a) | 11,07 | 11,43 | 11,78 | 12,11 | 12,40 | 12,65 | 12,86 | 13,01 | 13,11 |
| (b) | 11,07 | 11,22 | 11,36 | 11,51 | 11,65 | 11,79 | 11,94 | 12,08 | 12,22 |
| 7(a) | 12,59 | 12,94 | 13,27 | 13,59 | 13,88 | 14,15 | 14,38 | 14,58 | 14,73 |
| (b) | 12,59 | 12,73 | 12,87 | 13,00 | 13,14 | 13,27 | 13,41 | 13,55 | 13,68 |
| 8(a) | 14,07 | 14,40 | 14,72 | 15,03 | 15,32 | 15,60 | 15,84 | 16,06 | 16,25 |
| (b) | 14,07 | 14,20 | 14,33 | 14,46 | 14,59 | 14,72 | 14,85 | 14,98 | 15,11 |
| 9(a) | 15,51 | 15,83 | 16,14 | 16,44 | 16,73 | 17,01 | 17,26 | 17,49 | 17,70 |
| (b) | 15,51 | 15,63 | 15,76 | 15,89 | 16,02 | 16,14 | 16,27 | 16,40 | 16,52 |
| 10(a) | 16,92 | 17,23 | 17,54 | 17,83 | 18,12 | 18,39 | 18,65 | 18,89 | 19,11 |
| (b) | 16,92 | 17,04 | 17,17 | 17,29 | 17,41 | 17,54 | 17,66 | 17,79 | 17,91 |
| 11(a) | 18,31 | 18,61 | 18,91 | 19,20 | 19,48 | 19,76 | 20,02 | 20,26 | 20,49 |
| (b) | 18,31 | 18,43 | 18,55 | 18,67 | 18,79 | 18,91 | 19,04 | 19,16 | 19,28 |
| 12(a) | 19,68 | 19,97 | 20,26 | 20,55 | 20,83 | 21,10 | 21,36 | 21,61 | 21,84 |
| (b) | 19,68 | 19,79 | 19,91 | 20,03 | 20,15 | 20,27 | 20,39 | 20,51 | 20,63 |
| 13(a) | 21,03 | 21,32 | 21,60 | 21,89 | 22,16 | 22,43 | 22,69 | 22,94 | 23,18 |
| (b) | 21,03 | 21,14 | 21,26 | 21,38 | 21,50 | 21,62 | 21,74 | 21,85 | 21,97 |
| 14(a) | 22,36 | 22,65 | 22,93 | 23,21 | 23,48 | 23,75 | 24,01 | 24,26 | 24,50 |
| (b) | 22,36 | 22,48 | 22,60 | 22,71 | 22,83 | 22,95 | 23,06 | 23,18 | 23,30 |
| 15(a) | 23,68 | 23,97 | 24,24 | 24,52 | 24,79 | 25,05 | 25,31 | 25,56 | 25,80 |
| (b) | 23,68 | 23,80 | 23,92 | 24,03 | 24,15 | 24,26 | 24,38 | 24,50 | 24,61 |
| k | C1=4,5 | C1=5,0 | C1=6,0 | C1=7,0 | C1=8,0 | C1=9,0 | C1=10,0 | C1=12,0 | C1=14,0 |
| 3(a) | – | – | – | – | – | – | – | – | – |
| (b) | – | – | – | – | – | – | – | – | – |
| 4(a) | – | – | – | – | – | – | – | – | – |
| (b) | – | – | – | – | – | – | – | – | – |
| 5(a) | 11,21 | 11,02 | – | – | – | – | – | – | – |
| (b) | 10,87 | 11,02 | – | – | – | – | – | – | – |
| 6(a) | 13,14 | 13,10 | 12,78 | – | – | – | – | – | – |
| (b) | 12,36 | 12,50 | 12,78 | – | – | – | – | – | – |
| 7(a) | 14,83 | 14,88 | 14,81 | 14,49 | – | – | – | – | – |
| (b) | 13,82 | 13,95 | 14,32 | 14,49 | – | – | – | – | – |
| 8(a) | 16,40 | 16,51 | 16,60 | 16,49 | 16,16 | – | – | – | – |
| (b) | 15,25 | 15,38 | 15,64 | 15,90 | 16,16 | – | – | – | – |
| 9(a) | 17,88 | 18,03 | 18,22 | 18,26 | 18,12 | 17,79 | – | – | – |
| (b) | 16,65 | 16,78 | 17,03 | 17,29 | 17,54 | 17,79 | – | – | – |
| 10(a) | 19,31 | 19,48 | 19,75 | 19,89 | 19,89 | 19,73 | 19,40 | – | – |
| (b) | 18,04 | 18,16 | 18,41 | 18,66 | 18,91 | 19,16 | 19,40 | – | – |
| 11(a) | 20,70 | 20,89 | 21,21 | 21,42 | 21,52 | 21,49 | 21,32 | – | – |
| (b) | 19,40 | 19,52 | 19,77 | 20,01 | 20,26 | 20,50 | 20,75 | – | – |
| 12(a) | 22,06 | 22,27 | 22,62 | 22,88 | 23,06 | 23,12 | 23,07 | 22,56 | – |
| (b) | 20,75 | 20,87 | 21,12 | 21,36 | 21,60 | 21,64 | 22,08 | 22,56 | – |
| 13(a) | 23,40 | 23,62 | 23,99 | 24,30 | 24,53 | 24,66 | 24,70 | 24,44 | – |
| (b) | 22,09 | 22,21 | 23,45 | 22,69 | 22,92 | 23,16 | 23,40 | 23,88 | – |
| 14(a) | 24,73 | 24,95 | 25,34 | 25,68 | 23,93 | 26,14 | 26,25 | 26,17 | 25,66 |
| (b) | 23,42 | 23,53 | 23,77 | 24,00 | 24,24 | 24,48 | 24,74 | 25,19 | 25,65 |
| 15(a) | 26,04 | 26,26 | 26,67 | 27,03 | 27,33 | 27,56 | 27,73 | 27,80 | 27,50 |
| (b) | 24,73 | 24,85 | 25,08 | 25,31 | 25,55 | 23,78 | 26,01 | 26,48 | 26,95 |
Маркетинг, решение исследовательских задач
Алифанов А.Л., Алифанов Л.А. Маркетинг: Решение исследовательских задач: Учеб. Пособие. Красноярск, ИПЦ КГТУ, 2005. 95 с.
ОГЛАВЛЕНИЕ
Введение
- Проверка статистических гипотез
1.1. Предпосылки использования в маркетинговых исследованиях статистических методов
1.2. Оценка существенности факторов, влияющих на объем производства товара, с помощью непараметрического критерия знаков
1.3. Оценка значимости систематически действующих факторов на результат деятельности фирм с использованием критерия для количества серий
1.4. Анализ компьютерного рынка с позиций однородности объемов продаж лидирующими компаниями
1.5. Вычисление количественной оценки статистической связи между качественными показателями деятельности фирм
1.6. Оценивание резко выделяющихся показателей динамики реального денежного дохода населения
1.7. Проверка однородности выручки, получаемой от российского экспорта основных видов продукции
1.8. Оценка однородности условий маркетинговой деятельности
- Анализ факторов, обуславливающих успех управления маркетингом
2.1. Оценка значимости местонахождения пункта продаж на средние цены автомобилей
2.2. Влияние квалификации специалистов на продолжительность технического обслуживания машин
2.3. Оценка существенности влияния двух факторов и их взаимодействия на показатели маркетинга
- Непараметрические методы исследования в маркетинге
3.1. Экспертные методы оценивания качества товаров и услуг
3.2. Оценивание существенности влияния рейтинга марки товара на прибыль фирм
- Управление запасами
4.1. Термины, постановка задачи
4.2. Расчет оптимального размера партии при равномерном спросе
4.3. Расчет оптимального размера партии в случае модели производственных поставок
- Модели массового обслуживания
5.1. Термины, определения
5.2. Вычисление показателей простейшей очереди
Заключение
Библиографический список
Приложение
ВВЕДЕНИЕ
Маркетинг как вид человеческой деятельности, направленной на удовлетворение нужд и потребностей посредством обмена [7], подвержен влиянию огромного количества факторов демографического, экономического, природного, научно-техничес-кого, политического, культурного характера. Они проявляют себя в случайные моменты времени, в различных сочетаниях, с разной степенью воздействия на эффективность маркетинговой деятельности.
Стратегическое планирование, разработка годовых планов и маркетинговый контроль невозможны без знания рыночной ситуации и формирующих ее факторов макро- и микросреды. Поэтому необходимо выявление наиболее значимых их них с целью построения оптимизационных моделей и написания сценариев, позволяющих осуществлять последовательное и глубокое внедрение на рынки.
Маркетинговая ситуация быстро меняется, уровень значимости факторов, существенных в настоящий момент, через относительно малый промежуток времени может повыситься или снизиться; с развитием рынка на первое место могут выходить качественно новые факторы, коренным образом изменяя условия производства, сбыта и потребления.
В настоящем пособии изложены наиболее простые и эффективные способы, лежащие в основе формирования статистических банков – совокупностей «современных методик статистической обработки информации, позволяющих наиболее полно вскрыть взаимозависимости в рамках подборки данных и установить степень их статистической надежности» [7], а также банков моделей.
Как статистические банки, так и банки оптимизационных и прогнозных моделей требуют постоянного поддержания уровня их надежности за счет совершенствования самих методик и моделей. Изложенные в пособии методики и модели представляют собой фундаментальные знания, на основе которых осуществляется повышение уровня их эффективности.
В первой главе рассмотрены методы и примеры решения задач проверки статистических гипотез при исследовании различных аспектов маркетинговой деятельности с помощью критериев математической статистики. Приведены способы оценивания существенности факторов, влияющих на показатели маркетинга, и значимости систематически действующих факторов на результаты работы фирм. Представлены методы проверки однородности объемов продаж ведущими компаниями, оценки статистической связи между показателями функционирования организаций и резко выделяющихся показателей реального денежного дохода населения. Произведен анализ однородности выручки, получаемой от российского экспорта основных видов продукции, и однородности условий маркетинговой деятельности.
Вторая глава посвящена анализу факторов, обуславлива-ющих эффективность маркетинговой деятельности. Здесь приведены методика и решение задачи с помощью однофакторного дисперсионного анализа: оценка значимости влияния местонахождения пункта продаж на цены автомобилей, а также методика и решение задач с помощью двухфакторного дисперсионного анализа: оценка существенности влияния двух факторов и их взаимодействия на показатели маркетинга.
В третьей главе на примерах проиллюстрированы приемы применения непараметрических методов исследования в маркетинге для количественного оценивания качественных состояний или свойств объектов. Рассмотрены примеры выявления уровня надежности автомобильных узлов, а также уровни эффективности использования различных видов транспорта крупными отправителями. Изложены элементы кластерного анализа в свете оценивания существенности влияния рейтинга марки товара на прибыль фирм.
В четвертой главе изложен один из важнейших аспектов маркетинга – управление запасами. Приведены описание задач теории и способы определения оптимальных размеров партий товара для двух вариантов: в случае равномерного спроса и в случае модели производственных поставок.
В пятой главе рассмотрены понятия теории массового обслуживания и на примерах показаны варианты использования простейших моделей для вычисления основных показателей систем, находящих применение в различных сферах маркетинговой деятельности.
Изложение приведенных в данном пособии методик ориентировано на выполнение расчетов вручную. На практике более удобно осуществлять исследования в специализированных пакетах программ, либо программировать вычислительные алгоритмы самостоятельно, однако, в процессе обучения «ручной» счет предпочтительнее, так как помогает лучше усвоить материал и закрепить его понимание на интуитивном уровне.
Дата: 2018-12-28, просмотров: 766.