Линейная величина 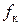 , измеряемая обычно в сантиметрах, называется коэффициентом трения качения.
, измеряемая обычно в сантиметрах, называется коэффициентом трения качения.
Найдём предельное значение тяги Sпр. В предельном положении момент пары трения качения равен моменту вращающей пары:
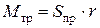 ,
,
где r - радиус катка.
Или
 .
.
Откуда находим
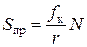 .
.
Качение начнется, если

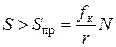 . (29)
. (29)
Качение будет происходить без скольжения, как было отмечено выше, если
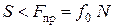 . (30)
. (30)
Итак, при качении без скольжения должны выполняться одновременно условия (29) и (30).
Для большинства материалов 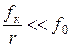 , что хорошо видно из таблицы
, что хорошо видно из таблицы
Поэтому 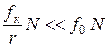 и, следовательно, условия (29) и (30) не противоречат друг другу.
и, следовательно, условия (29) и (30) не противоречат друг другу.
Таблица Коэффициенты трения скольжения и качения
| № п/п | Материалы тела | Коэффициент трения скольжения | Материалы тела | Коэффициент трения качения |
| 1. | Сталь по стали | 0,015 | Сталь закаленная по стали (шариковый подшипник) | 0,001 |
| 2. | Сталь по чугуну | 0,30 | Мягкая сталь по стали (колесо по рельсу) | 0,005 |
| 3. | Мягкая сталь по чугуну | 0,20 | ||
| 4. | Сталь по бронзе | 0,15 | ||
| 5. | Мягкая сталь по бронзе | 0,80 | ||
| 6. | Дерево по дереву | 0,40- 0,60 | Дерево по дереву | 0,05- 0,08 |
Окончательно получаем, что при качении без скольжения тяга S должна удовлетворять условиям
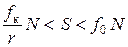 .
.
Откуда видно, что привести каток в качение значительно легче, чем привести его в скольжение. Этим объясняется то, что в технике, когда это возможно, стремятся заменить скольжение качением (колеса, катка, шариковые подшипники и т.п.).
Итак, реакция опорной поверхности при качении тела без скольжения состоит из:
1) нормальной реакции 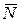 ;
;
2) силы трения 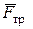 , препятствующей скольжению;
, препятствующей скольжению;
3) пары трения качения с моментом 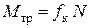 , препятствующей вращению тела.
, препятствующей вращению тела.
Найдем работу названных сил и пары.
Так как при качении без скольжения скорость точки касания тела с опорой равна нулю ( 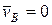 ), то
), то
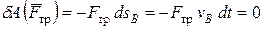 ,
, 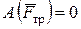 .
.
Очевидно, что
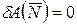 ,
, 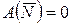
Далее, элементарная работа пары трения качения определяется формулой
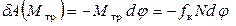 .
.
Или
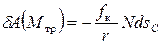 ,
,
где 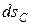 - элементарное перемещение центра С катка.
- элементарное перемещение центра С катка.
Полная работа пары трения качения определяется интегралом
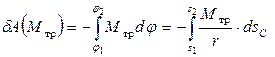 .
.
В случае 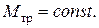 полная работа будет равна
полная работа будет равна
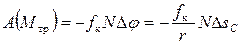 ,
,
где 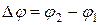 ,
, 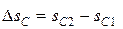 .
.
Задачи
Теорему об изменении кинетической энергии механической системы целесообразно применять к решению задач, в которых рассматривается движение механической системы с одной степенью свободы, а реакции наложенных на нее связей не совершают работу.
С помощью теоремы об изменении кинетической энергии в интегральной форме легко решаются задачи на определение скоростей (линейных и угловых), когда известны перемещения и действующие силы (они должны быть постоянными или зависящими только от перемещений).
Дифференциальная форма теоремы об изменении кинетической энергии применяется для определения ускорений (линейных или угловых), а также для составления дифференциального уравнения движения механической системы.
Если механическая система состоит из абсолютно твёрдых тел, соединенных нерастяжимыми нитями и шарнирами, причем трение сочлененных тел не учитывается, то для такой системы достаточно изобразить только внешние силы, так как работа внутренних сил в этом случае будет равна нулю
Дата: 2019-02-02, просмотров: 322.