Работа силы трения скольжения
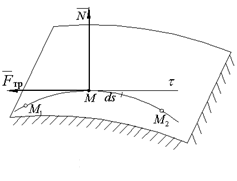
Изобразим поверхность по которой движется точка М.
Пусть материальная точка М движется по шероховатой поверхности.
Сила трения скольжения определяется формулой
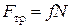 ,
,
где f - динамический коэффициент трения;
N - нормальная реакция поверхности.
 |
Сила 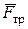 будет совершать отрицательную работу.
будет совершать отрицательную работу.
Воспользуемся формулой (11)
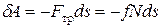 .
.
Работа силы трения на конечном перемещении равна
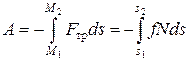 .
.
В случае, когда 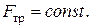 , получаем
, получаем
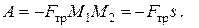 (17)
(17)
Работа силы трения зависит от длины дуги траектории точки. Эта сила не является потенциальной.
Теперь необходимо определить работу сил приложенных к твердому телу.
Сначала получим выражения для определения работы внутренних сил, а потом внешних.
Работа внутренних сил абсолютно твердого тела
Выделим в твердом теле две произвольные точки M1 и M2.
Cилы взаимодействия между ними являются внутренними силами, которые согласно третьему закону Ньютона равны по модулю и направлены по одной прямой l в противоположные стороны :
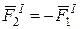 .
.
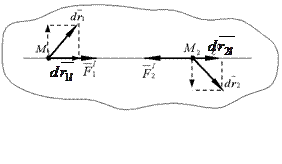
Будем считать, что тело совершает произвольное движение.
Изобразим перемещение точек М1 и М2
Составляем сумму элементарных работ этих сил на любом бесконечно малом перемещении тела
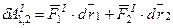 .
.
Представим перемещения 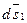 и
и 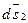 в виде двух составляющих, одна из которых направлена по прямой l, а вторая перпендикулярна к этой прямой.
в виде двух составляющих, одна из которых направлена по прямой l, а вторая перпендикулярна к этой прямой.
Так как рассматриваемые силы не совершают работу на перпендикулярных к ним перемещениях, то последняя формула принимает вид
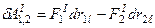
Для абсолютно твердого тела его точки не могут ни удалиться друг от друга, ни приближаться друг к другу. Поэтому
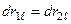 .
.
Если к тому же учесть, что 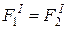 , то получаем для любой пары точек тела
, то получаем для любой пары точек тела
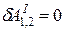 (18)
(18)
и тем самым
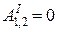 . (19)
. (19)
В результате суммирования выражений (18) и (19) по всем парам материальных точек, получаем для всего твердого тела
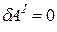 ,
, 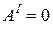 .
.
Сумма работ всех внутренних сил абсолютно твердого тела на любом его перемещении равна нулю.
Это выражение справедливо только для абсолютно твердых тел. Если же система реальная, то под действием внутренних сил точки будут как-то перемещаться и работа внутренних сил будет равна нулю.
Работа и мощность внешних сил, приложенных к твердому телу.
Поступательное движение тела.
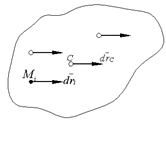 Изображаем тело, изображаем точку C и ее перемещение
Изображаем тело, изображаем точку C и ее перемещение 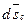 , затем изображаем точку М i
, затем изображаем точку М i
Вычислим выражение для мощности всех сил, приложенных к поступательно движущемуся телу
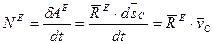 . (21)
. (21)
Мощность в этом случае равна скалярному произведению главного вектора всех внешних сил на вектор скорости центра масс тела.
Вращательное движение тела вокруг
Неподвижной оси.
Изображаем тело, которое вращается вокруг неподвижной оси., с угловой скоростью ω. Выбираем точку М i, она движется по окружности с радиусом hi, d j - элементарный угол поворота, дугу соответствующую углу обозначим 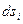 .
.
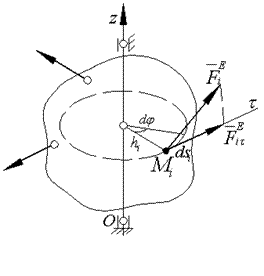 К точке М прикладываем силу.
К точке М прикладываем силу.
Теперь изобразим проекцию этой силы на касательную. 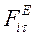 и запишем формулу для вычисления элементарной работы6
и запишем формулу для вычисления элементарной работы6
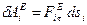 .
.
Так как 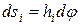 ,
,
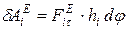 .
.
где
h i - расстояние точки M1 от оси вращения,
d j - элементарный угол поворота, то
Отметим, что
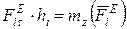 .
.
Таким образом
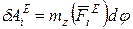 .
.
Элементарная работа всех сил будет равна
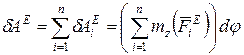 ,
,
или
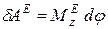 , (22)
, (22)
где 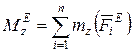 - главный момент всех внешних сил относительно оси вращения.
- главный момент всех внешних сил относительно оси вращения.
M - масса катка
С – центр масс
Опора шероховатая
Пусть к его оси , приложена сила 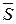 , которую будем называть тягой.
, которую будем называть тягой.
Работу этих сил.
8.2 Определение сил сопротивления.
Определяем активные силы.
Первой активной силой является сила тяжести.
Второй силой будет являться сила тяги
Сила трения 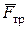 будет препятствовать скольжению катка. Причиной появления этой силы является шероховатость соприкасающихся поверхностей.
будет препятствовать скольжению катка. Причиной появления этой силы является шероховатость соприкасающихся поверхностей.
При отсутствии скольжения эта сила по модулю равна тяге 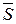 :
:
Fтр = S.
Нормальная реакция 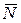 по модулю равна весу катка:
по модулю равна весу катка:
N = P.
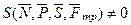 .- не уравновешенная
.- не уравновешенная
Силы 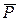 и
и 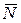 уравновешивают друг друга, а силы
уравновешивают друг друга, а силы 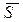 и
и 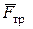 образуют пару:
образуют пару:
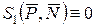 ,
, 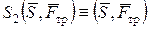 - с плечом R
- с плечом R
Следовательно, под действием пары 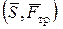 каток должен вращаться при сколь угодно малой тяге S.
каток должен вращаться при сколь угодно малой тяге S.
Задачи
Теорему об изменении кинетической энергии механической системы целесообразно применять к решению задач, в которых рассматривается движение механической системы с одной степенью свободы, а реакции наложенных на нее связей не совершают работу.
С помощью теоремы об изменении кинетической энергии в интегральной форме легко решаются задачи на определение скоростей (линейных и угловых), когда известны перемещения и действующие силы (они должны быть постоянными или зависящими только от перемещений).
Дифференциальная форма теоремы об изменении кинетической энергии применяется для определения ускорений (линейных или угловых), а также для составления дифференциального уравнения движения механической системы.
Если механическая система состоит из абсолютно твёрдых тел, соединенных нерастяжимыми нитями и шарнирами, причем трение сочлененных тел не учитывается, то для такой системы достаточно изобразить только внешние силы, так как работа внутренних сил в этом случае будет равна нулю
Работа силы трения скольжения
Изобразим поверхность по которой движется точка М.
Пусть материальная точка М движется по шероховатой поверхности.
Сила трения скольжения определяется формулой
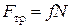 ,
,
где f - динамический коэффициент трения;
N - нормальная реакция поверхности.
 |
Сила 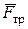 будет совершать отрицательную работу.
будет совершать отрицательную работу.
Воспользуемся формулой (11)
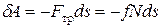 .
.
Работа силы трения на конечном перемещении равна
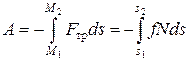 .
.
В случае, когда 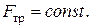 , получаем
, получаем
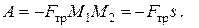 (17)
(17)
Дата: 2019-02-02, просмотров: 355.