Регулярный поток:

Здесь , что и обозначено на рис.1.10. Из теории вероятностей известно, что плотность вероятности неслучайной величины определяется дельта-функцией.

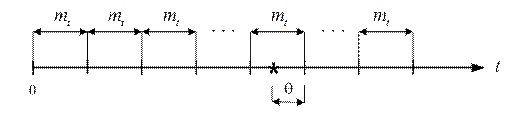
Рис.1.10. Регулярный поток.

Поэтому для постоянного интервала 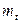 можно записать

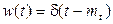                              .                        (1.46)

Напомним здесь основные свойства дельта-функции.

     1. Фильтрующее свойство. Если 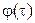- произвольная функция (без разрывов в 0), то справедливо соотношение

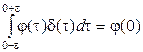. Здесь  – малая константа.  

     2. При 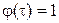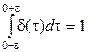. Естественно, что и в бесконечных пределах интегрирования результат будет такой же. Это позволяет утверждать, что дельта-функция как плотность вероятности удовлетворяет условию нормировки.

     3. 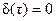 при .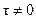

     4. .

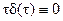Вернемся к регулярному потоку. Для него очевидно 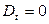. Найдём плотность вероятности интервала, на который падает точка S

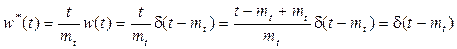. (1.47)

Как видно из (1.47) случайная точка S никак не изменяет вероятностные свойства интервала, на который она попадает. Найдём закон распределения времени q от случайной точки до очередного события

       . (1.48)

Получился равномерный закон для плотности вероятности. В этом нет ничего удивительного, если вспомнить, что при падении точки S было предположено, что она с равной вероятностью может попасть в любой бесконечно малый промежуток интервала Т^*. Найдём числовые характеристики распределения (1.48).

Из формулы (1.26)         .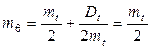          

Из формулы (1.27)     .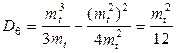

Характеристическая функция:

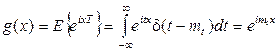                   .         (1.49)

Регулярный поток для моделирования потока событий используется редко, так как он обладает неограниченным последействием, т.е., зная лишь один момент наступления события в регулярном потоке, можно восстановить всё прошлое и предсказать всё будущее потока.

Нормальный поток.

По определению одномерная нормальная плотность вероятности имеет вид (формула записана применительно к случайной величине Т ):

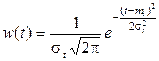                          .                         (1.50)

В (1.50) 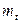- среднее значение и 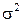- дисперсия распределения. График нормальной плотности приведен на рис.1.11.

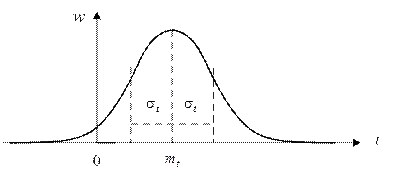
Рис.1.11. График нормальной плотности вероятности.

Строго говоря, интервал времени не может быть распределён по нормальному закону, так как область определения нормального закона 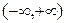. Однако, если выполняется условие 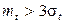, то этот закон можно приближенно использовать.

Устремим 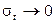. Тогда из (1.50) следует:  

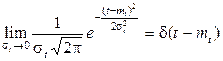                         .              (1.51)

Плотность распределения интервала, на который случайным образом упала точка S:

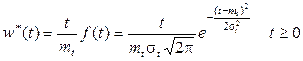                .           (1.52)

Соответственно плотность вероятности интервала от точки S до наступления очередного события имеет вид

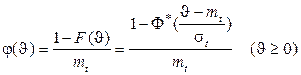                 ,       (1.53)

где

                               .                     (1.54)

Характеристическая функция нормального распределения

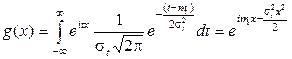                 .        (1.55)

Поток Эрланга

Поток Эрланга получается путём особого преобразования («разрежения») простейшего потока. Это преобразование осуществляется путём выбрасывания некоторых событий из простейшего потока. Процесс «разрежения» потока поясняется на рис.1.12, где буквой П обозначен простейший поток.

Если выбрасывается каждая вторая точка, то получается Э₁ – поток Эрланга первого порядка. Если выбрасывается два события подряд и оставляется каждое третье, то получается Э₂ – поток Эрланга второго порядка и т.д.

Потоком Эрланга k -го порядка называется поток Пальма, у которого интервалы между событиями представляют собой сумму ( k +1) независимых случайных величин, распределённых одинаково по экспоненциальному закону с параметром 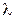, где 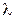 - интенсивность простейшего потока и  

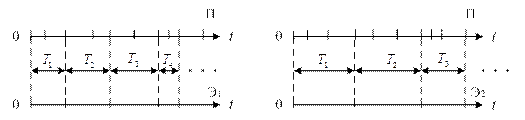
Рис.1.12. «Разрежение» простейшего потока.

При  получается исходный простейший поток П.

Для простейшего потока характеристическая функция интервала времени между соседними событиями определяется в виде . Из свойств характеристической функции следует, что для суммы  независимых интервалов характеристическая функции будет иметь вид. . Поэтому для Э_k можно записать .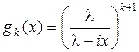 

Совершая обратный переход от характеристической функции к плотности вероятности, получим для Э_k:

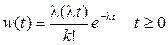                             .                (1.56)

Функция распределения для этой плотности имеет вид

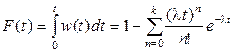                     .               (1.57)

Соответственно числовые характеристики определяются как                         ,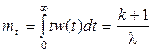

                        .

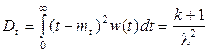При достаточно большом k (k>5) поток Э_k можно считать приближённо нормальным. Это следует из того, что в Э_k суммируется k+1 независимых величин (интервалов), распределённых одинаково, а такая сумма согласно центральной предельной теореме теории вероятностей (ЦПТ) при 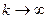 асимптотически нормальна.