Пуассоновский поток – это поток обладающий двумя свойствами – ординарностью и отсутствием последействия.
Понятие ординарности было объяснено выше, а свойство отсутствия последействия можно сформулировать следующим образом: для двух неперекрывающихся интервалов времени число событий, попадающих в один интервал, не зависит от того, сколько событий попало в другой.
Пусть дан стационарный поток с интенсивностью 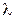 . Из ординарности потока следует:
. Из ординарности потока следует:
- вероятность наступления одного события за время  :
: 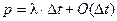
- вероятность ненаступления события 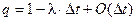
Рассмотрим интервал 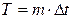 , представленный на рис. 1.6. Из независимости (отсутствия последействия) событий на соседних интервалах следует, что вероятность наступления k событий на m интервалах определяется биномиальной формулой:
, представленный на рис. 1.6. Из независимости (отсутствия последействия) событий на соседних интервалах следует, что вероятность наступления k событий на m интервалах определяется биномиальной формулой:
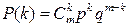 , (1.28)
, (1.28)
где число сочетаний 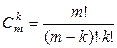 .
.
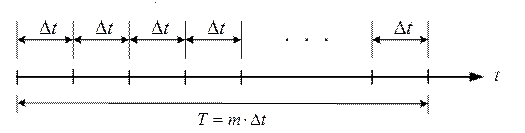
Рис. 1.6. К определению пуассоновского потока событий.
Для вычисления факториалов используем формулу Стирлинга
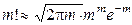 (1.29)
(1.29)
(при m=1 ошибка вычислений по (1.29) составляет 8%, при m=100 ошибка - 0,08%), а для вычисления 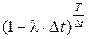 при
при
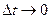 - второй замечательный предел
- второй замечательный предел 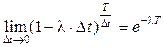 .
.
С учетом сделанных замечаний формула (1.28) преобразуется к виду
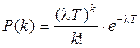 , (1.30) и именно в таком виде она известна как распределение Пуассона, где k=0,1,2,... Вид этого дискретного распределения приведен на рис.1.7.
, (1.30) и именно в таком виде она известна как распределение Пуассона, где k=0,1,2,... Вид этого дискретного распределения приведен на рис.1.7.
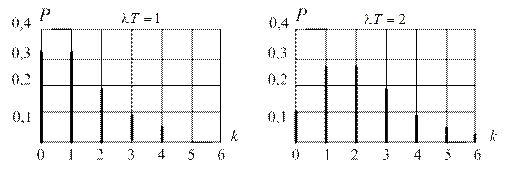
Рис.1.7. Распределение Пуассона
Заметим, что распределение Пуассона удовлетворяет ус-ловию нормировки 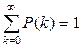 .
.
В случае нестационарного потока распределение Пуассо-на записывается в виде:
 , (1.31)
, (1.31)
где 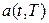 -среднее число событий, наступающих на интервале T, примыкающем к моменту t ,
-среднее число событий, наступающих на интервале T, примыкающем к моменту t ,
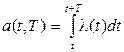 ,
,
а  - интенсивность нестационарного потока.
- интенсивность нестационарного потока.
В стационарном случае 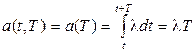 и получа-ется формула (1.30).
и получа-ется формула (1.30).
Найдем среднее и дисперсию распределения Пуассона. Среднее:
 . (1.32)
. (1.32)
Вычисление (1.32) иллюстрируется следующими соотношения-ми (с учетом условия нормировки)
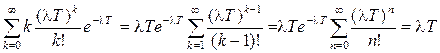 .
.
Дисперсия:
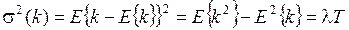 . (1.33)
. (1.33)
Здесь необходимо отметить, что распределение Пуассона обладает уникальным свойством – равенством среднего и дисперсии, - что отличает его от всех известных распределений и может служить признаком при идентификации распределения на практике. Из отношения
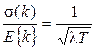
следует, что при больших 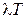 распределение тесно группиру-ется около среднего. Оценкой l может служить величина
распределение тесно группиру-ется около среднего. Оценкой l может служить величина 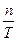 , где n - измеренное на практике число событий на интервале Т.
, где n - измеренное на практике число событий на интервале Т.
Стационарный пуассоновский поток событий называет-ся простейшим потоком.
Рассмотрим теперь интервалы времени t (см. рис.1.8) между событиями в стационарном пуассоновском потоке, которые представляют собой непрерывные случайные величины.
Возьмем начальный интервал времени (он ничем не отличается от всех остальных), и отметим после 0 некоторую точку x . На интервале (0, x) не будет ни одного события, если 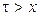 .
.
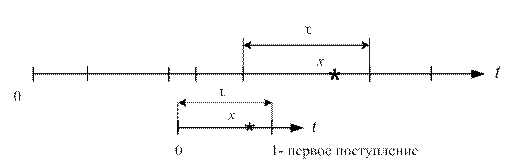
Рис.1.8. Анализ интервалов времени в пуассоновском потоке
Вероятность выполнения этого неравенства может быть вычислена по формуле (1.30) для 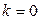 с учетом того, что х=Т
с учетом того, что х=Т
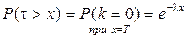 .
.
Далее: 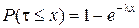
Последнее выражение - это (по определению) функция распределения случайной величины t , т.е. 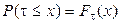 . Но тогда
. Но тогда
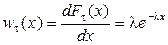 , (1.34)
, (1.34)
т.е. для пуассоновского потока t имеет экспоненциальное расп-ределение для 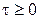 (см. рис. 1.9).
(см. рис. 1.9).
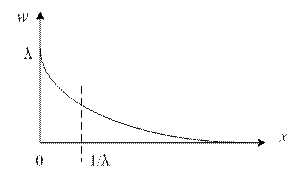
Рис.1.9. Экспоненциальное распределение.
Характеристики экспоненциального распределения:
среднее -  ,
,
дисперсия - 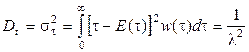 .
.
Если случайная точка S попадает на интервал 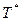 между событиями в пуассоновском потоке (см. предыдущий параграф), то
между событиями в пуассоновском потоке (см. предыдущий параграф), то
 . (1.35)
. (1.35)
Формула (1.35) – это распределение Эрланга 1-го порядка. При этом согласно формулам (1.17), (1.18) получим
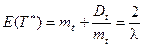
 и
и 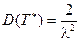 .
.
Сравнивая 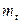 и
и 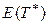 , а так же
, а так же 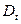 и
и 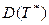 , можно утверж-дать, что наличие случайной точки S в каком-либо интервале пуассоновского потока “раздвигает” его, увеличивая среднее и дисперсию вдвое.
, можно утверж-дать, что наличие случайной точки S в каком-либо интервале пуассоновского потока “раздвигает” его, увеличивая среднее и дисперсию вдвое.
Теперь найдем  для пуассоновского потока.
для пуассоновского потока.
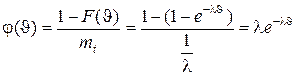 , (1.36)
, (1.36)
что совпадает с экспоненциальным распределением, спра-ведливым для интервала времени между событиями в пуассоновском потоке, т.е. случайная величина q распределена так же, как и T . Это является формой проявления свойства отсутствия последействия. Любая информация о том, как вел себя поток до точки S, не дает нам сведений о том, что произойдет после точки S.
Вычислим характеристическую функцию интервала между соседними событиями в простейшем потоке.
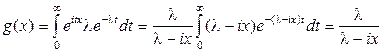 . (1.37)
. (1.37)
Итак, поток Пальма является простейшим, если характеристическая функция интервала между соседними событиями равна 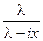 .
.
В заключение отметим одно важное свойство пуассоновского процесса. Пусть есть m пуассоновских потоков с интенсивностями 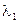 ,
, 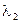 , …
, … 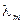 . Объединим эти потоки. Тогда объединенный поток будет опять пуассоновский с интенсивностью
. Объединим эти потоки. Тогда объединенный поток будет опять пуассоновский с интенсивностью 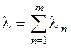 . Покажем справедливость этого утверждения.
. Покажем справедливость этого утверждения.
Пусть 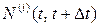 - число событий i-го процесса в промежутке
- число событий i-го процесса в промежутке 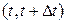 , i=1,2…m.
, i=1,2…m. 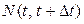 - число событий в объединенном процессе.
- число событий в объединенном процессе.
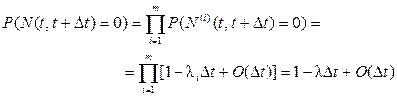 ,
,
где 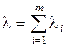 . Ответ становится очевидным, если учесть, что
. Ответ становится очевидным, если учесть, что  в степени выше первой является величиной высшего порядка малости по сравнению с
в степени выше первой является величиной высшего порядка малости по сравнению с  .
.
Аналогично: 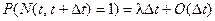 .
.
Дата: 2019-02-02, просмотров: 379.