Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

В.Г. Карташевский

Основы теории массового

Обслуживания

Рекомендовано УМО по образованию в области телекоммуникаций в качестве учебного пособия для студентов высших учебных заведений, обучающихся по направлению подготовки дипломированных специалистов 210400 (654400) - Телекоммуникации

	Радио и связь

	Москва 2006

 

 

УДК 621.391

К27

Карташевский В.Г.

Основы теории массового обслуживания : Учебное пособие для вузов.- М.: Радио и связь, 2006.- 86с.: 34ил.

  ISBN 5-256-1808-6

 

Освещаются основы теории массового обслуживания, знание которых необходимо для современного представления о процессах распределения информации в телекоммуни-кационных и вычислительных сетях.

       Рассматриваются потоки заявок на обслуживание, при условии, что структура потока носит случайный характер. Особое внимание уделено пуассоновскому потоку событий.

       Проанализирована работа устройств массового обслуживания (в обозначении Кендалла) типа М/М/1, M/G/1, G/M/1 и их модификаций. Рассмотрены системы с относительным приоритетом обслуживания.

       Для студентов вузов, обучающихся по специальностям направления «Телекоммуникации», может быть полезна специалистам в области связи.

 

ИБ № 3142

ISBN 5-256-1808-6

Издательская лицензия № 010164 от 29.01.97г.

 

Оглавление

Оглавление      .    .    .    .    .    .    .   3

Введение .    .    .    .    .    .    .    .   4

1. Потоки событий   .    .    .    .    .    .    7

1.1. Основные определения  .    .    .    .    7

1.2. Закон распределения времени, на который

        падает точка .    .    .    .    .    .    9

1.3. Закон распределения времени до наступления

        очередного события .    .    .    .    .    14

1.4. Пуассоновский поток событий .    .    .    18

       Анализ интервалов времени в пуассоновском

        потоке .    .    .    .    .    .    .    21

1.5. Вывод формулы Пуассона через производящую   

        функцию .    .    .    .    .    .    .    24

1.6. Другие стационарные потоки Пальма .    .    27

       Регулярный поток .    .    .    .    .    27

        Нормальный поток .    .    .    .    .    29

        Поток Эрланга      .    .    .    .    .    30

        Предельная теорема для суммарного потока .    32

        Предельная теорема для редеющего потока .    33

2. Анализ систем массового обслуживания   .    .    37

2.1. Классификация систем  .    .    .    .    37

2.2. Система обслуживания М/М/1 .    .    .    39

     Вероятность блокировки .    .    .    .    44

2.3. Формула Литтла    .    .    .    .    .    48

2.4. Системы обслуживания, зависящие от состояний 52  

        Система M/M/2   .    .    .    .    .    54

     Система М/М/¥   .    .    .    .    .    57 Система с нетерпеливыми клиентами .    .    58    

        Система M/M/N/0 .    .    .    .    .    60    

2.5. Система обслуживания M/G/1 .    .    .    62 Система M/D/1     .    .    .    .    .    66   

2.6. Упрощенный вывод формулы для Е( n ) системы

        M/G/1 .    .    .    .    .    .    .    71

2.7. Система G/M/1    .    .    .    .    .    74

2.8. Системы обслуживания с относительными

        приоритетами .    .    .    .    .    .    79

       Литература .    .    .    .    .    .    86

Введение.

Ежедневно мы сталкиваемся с ситуациями, в которых появляется потребность в массовом обслуживании. Самым простым примером такой ситуации является очередь в магазине или на остановке автобуса, которая появляется из-за того, что у тех, кто занимается обслуживанием, нет возможности обслужить всех сразу. Не случайно, в публикациях на английском языке теорию массового обслуживания называют теорией очередей. Можно привести множество примеров, когда проявляются проблемы массового обслуживания - невозможность дозвониться по нужному номеру, скопление самолётов над аэродромом из-за отсутствия посадочных полос, обслуживание группы станков одним рабочим, ремонт судов при ограниченном числе доков, перевозка грузов автотранспортной конторой и т.д.

Примеры разные, но им присущи формальные признаки, которые позволяют описать их с помощью одного и того же математического аппарата. Главная задача, стоящая перед теорией – установить с необходимой точностью количественную связь между числом приборов обслуживания, характеристиками входящего потока требований (заявок) на обслуживание и качеством обслуживания. Под качеством обслуживания в теории массового обслуживания обычно понимается своевременность обслуживания поступивших в систему требований. Естественно, качество обслуживания надо уметь оценивать количественно.

Общая особенность всех задач теории массового обслуживания – случайный характер исследуемых явлений. Действительно, количество требований на обслуживание (например, число звонков, поступающих на телефонную станцию за фиксированный промежуток времени) – случайная величина. Временной интервал между поступлением требований – случайная величина. И, наконец, время обслуживания каждой заявки – также случайная величина. Поэтому решение всех задач массового обслуживания основывается на методах теории вероятностей.

Рассмотрим основные элементы системы массового обслуживания, которые представлены на рис. В.1.

 

 

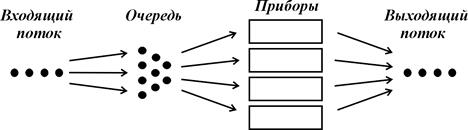
Рис.В.1. Основные элементы системы массового обслуживания.

Входящий поток – совокупность требований на обслуживание, поступивших в систему за определенный интервал времени. Требование – это запрос на удовлетворение потребности. Требование часто отождествляется с его носителем. Если речь идет о потоке данных для обработки на ЭВМ, то требованиями могут считаться пакеты данных. В качестве требований в очереди в парикмахерской могут рассматриваться сами клиенты, в потоке больных в приёмном покое больницы – больные и в потоке приходящих на разгрузку в порт судов – сами суда.

Системы обслуживания определяются числом приборов и бывают одноканальные и многоканальные (одна или несколько колонок на бензозаправке и т.д.). Многоканальные системы могут состоять из разнотипных приборов.

Системы бывают полнодоступные и неполнодоступные (обслуживающие приборы или каналы доступны любому требованию – это полнодоступное включение). Полно-доступность и неполнодоступность иллюстрируется рис.В.2. Если использовать аналогии с телефонной связью, то, например, линия «а» доступна абонентам А и В, линия «с» доступна абонентам А и Д, а линия «е» доступна абонентам А, В, С, Д, т.е. всем абонентам.

 

 

 

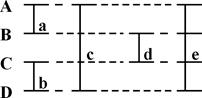
Рис.В.2. Полнодоступное и неполнодоступное включение.

 

Важным фактором, определяющим работу системы массового обслуживания, является способ обслуживания. Различают способы - в порядке поступления (FIFO), в обратном порядке (LIFO), случайным образом, обслуживание по приоритетам и ряд других. Возможно объединение очередей, взаимодействие очередей и т.д.

Способ обслуживания тесно связан с  поведением клиента – отказ становиться в очередь, использование клиентом априорной информации, уход из очереди до начала обслуживания (соглашение между клиентами) и т.д.

Обозначенный на рис.В.1 выходящий поток, как элемент системы массового обслуживания важен, так как сам может быть входящим потоком для другой системы. Характеристики выходящего потока зависят от характеристик входящего потока и времени обслуживания (если в парик-махерской два мастера с разной производительностью, то это будет влиять и на входящий и на выходящий поток). Анализ выходящего потока позволяет найти характеристики обслуживающих приборов.

В заключение подчеркнем еще раз, что под качеством обслуживания в теории массового обслуживания понимается не то, как хорошо выполнено обслуживание (бритьё, качество ремонта и др.), а как хорошо организовано обслуживание, насколько полно загружены приборы, не создаётся ли большая очередь, велик ли уход не обслуженных требований.

 

Потоки событий.

1.1. Основные определения.

Поток событий – последовательность событий, происхо-дящих одно за другим в случайные моменты времени. Графически поток можно отобразить так, как показано на рис.1.1, где на оси времени отмечено начало наблюдения 0 и моменты наступления событий ,  

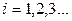
Рис.1.1. Графическое отображение потока событий

Поток Эрланга

Поток Эрланга получается путём особого преобразования («разрежения») простейшего потока. Это преобразование осуществляется путём выбрасывания некоторых событий из простейшего потока. Процесс «разрежения» потока поясняется на рис.1.12, где буквой П обозначен простейший поток.

Если выбрасывается каждая вторая точка, то получается Э₁ – поток Эрланга первого порядка. Если выбрасывается два события подряд и оставляется каждое третье, то получается Э₂ – поток Эрланга второго порядка и т.д.

Потоком Эрланга k -го порядка называется поток Пальма, у которого интервалы между событиями представляют собой сумму ( k +1) независимых случайных величин, распределённых одинаково по экспоненциальному закону с параметром 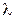, где 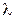 - интенсивность простейшего потока и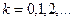  

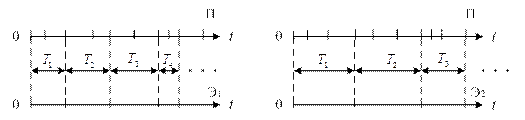
Рис.1.12. «Разрежение» простейшего потока.

 

При 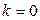 получается исходный простейший поток П.

Для простейшего потока характеристическая функция интервала времени между соседними событиями определяется в виде . Из свойств характеристической функции следует, что для суммы 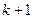 независимых интервалов характеристическая функции будет иметь вид. . Поэтому для Э_k можно записать .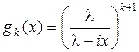 

Совершая обратный переход от характеристической функции к плотности вероятности, получим для Э_k:

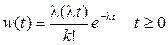                             .                (1.56)

Функция распределения для этой плотности имеет вид

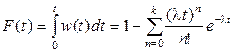                     .               (1.57)

Соответственно числовые характеристики определяются как                         ,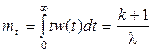

                        .

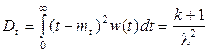При достаточно большом k (k>5) поток Э_k можно считать приближённо нормальным. Это следует из того, что в Э_k суммируется k+1 независимых величин (интервалов), распределённых одинаково, а такая сумма согласно центральной предельной теореме теории вероятностей (ЦПТ) при 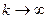 асимптотически нормальна.

В.Г. Карташевский

Основы теории массового

Обслуживания

Рекомендовано УМО по образованию в области телекоммуникаций в качестве учебного пособия для студентов высших учебных заведений, обучающихся по направлению подготовки дипломированных специалистов 210400 (654400) - Телекоммуникации

	Радио и связь

	Москва 2006

 

 

УДК 621.391

К27

Карташевский В.Г.

Основы теории массового обслуживания : Учебное пособие для вузов.- М.: Радио и связь, 2006.- 86с.: 34ил.

  ISBN 5-256-1808-6

 

Освещаются основы теории массового обслуживания, знание которых необходимо для современного представления о процессах распределения информации в телекоммуни-кационных и вычислительных сетях.

       Рассматриваются потоки заявок на обслуживание, при условии, что структура потока носит случайный характер. Особое внимание уделено пуассоновскому потоку событий.

       Проанализирована работа устройств массового обслуживания (в обозначении Кендалла) типа М/М/1, M/G/1, G/M/1 и их модификаций. Рассмотрены системы с относительным приоритетом обслуживания.

       Для студентов вузов, обучающихся по специальностям направления «Телекоммуникации», может быть полезна специалистам в области связи.

 

ИБ № 3142

ISBN 5-256-1808-6

Издательская лицензия № 010164 от 29.01.97г.

 

Оглавление

Оглавление      .    .    .    .    .    .    .   3

Введение .    .    .    .    .    .    .    .   4

1. Потоки событий   .    .    .    .    .    .    7

1.1. Основные определения  .    .    .    .    7

1.2. Закон распределения времени, на который

        падает точка .    .    .    .    .    .    9

1.3. Закон распределения времени до наступления

        очередного события .    .    .    .    .    14

1.4. Пуассоновский поток событий .    .    .    18

       Анализ интервалов времени в пуассоновском

        потоке .    .    .    .    .    .    .    21

1.5. Вывод формулы Пуассона через производящую   

        функцию .    .    .    .    .    .    .    24

1.6. Другие стационарные потоки Пальма .    .    27

       Регулярный поток .    .    .    .    .    27

        Нормальный поток .    .    .    .    .    29

        Поток Эрланга      .    .    .    .    .    30

        Предельная теорема для суммарного потока .    32

        Предельная теорема для редеющего потока .    33

2. Анализ систем массового обслуживания   .    .    37

2.1. Классификация систем  .    .    .    .    37

2.2. Система обслуживания М/М/1 .    .    .    39

     Вероятность блокировки .    .    .    .    44

2.3. Формула Литтла    .    .    .    .    .    48

2.4. Системы обслуживания, зависящие от состояний 52  

        Система M/M/2   .    .    .    .    .    54

     Система М/М/¥   .    .    .    .    .    57 Система с нетерпеливыми клиентами .    .    58    

        Система M/M/N/0 .    .    .    .    .    60    

2.5. Система обслуживания M/G/1 .    .    .    62 Система M/D/1     .    .    .    .    .    66   

2.6. Упрощенный вывод формулы для Е( n ) системы

        M/G/1 .    .    .    .    .    .    .    71

2.7. Система G/M/1    .    .    .    .    .    74

2.8. Системы обслуживания с относительными

        приоритетами .    .    .    .    .    .    79

       Литература .    .    .    .    .    .    86

Введение.

Ежедневно мы сталкиваемся с ситуациями, в которых появляется потребность в массовом обслуживании. Самым простым примером такой ситуации является очередь в магазине или на остановке автобуса, которая появляется из-за того, что у тех, кто занимается обслуживанием, нет возможности обслужить всех сразу. Не случайно, в публикациях на английском языке теорию массового обслуживания называют теорией очередей. Можно привести множество примеров, когда проявляются проблемы массового обслуживания - невозможность дозвониться по нужному номеру, скопление самолётов над аэродромом из-за отсутствия посадочных полос, обслуживание группы станков одним рабочим, ремонт судов при ограниченном числе доков, перевозка грузов автотранспортной конторой и т.д.

Примеры разные, но им присущи формальные признаки, которые позволяют описать их с помощью одного и того же математического аппарата. Главная задача, стоящая перед теорией – установить с необходимой точностью количественную связь между числом приборов обслуживания, характеристиками входящего потока требований (заявок) на обслуживание и качеством обслуживания. Под качеством обслуживания в теории массового обслуживания обычно понимается своевременность обслуживания поступивших в систему требований. Естественно, качество обслуживания надо уметь оценивать количественно.

Общая особенность всех задач теории массового обслуживания – случайный характер исследуемых явлений. Действительно, количество требований на обслуживание (например, число звонков, поступающих на телефонную станцию за фиксированный промежуток времени) – случайная величина. Временной интервал между поступлением требований – случайная величина. И, наконец, время обслуживания каждой заявки – также случайная величина. Поэтому решение всех задач массового обслуживания основывается на методах теории вероятностей.

Рассмотрим основные элементы системы массового обслуживания, которые представлены на рис. В.1.

 

 

Рис.В.1. Основные элементы системы массового обслуживания.

Входящий поток – совокупность требований на обслуживание, поступивших в систему за определенный интервал времени. Требование – это запрос на удовлетворение потребности. Требование часто отождествляется с его носителем. Если речь идет о потоке данных для обработки на ЭВМ, то требованиями могут считаться пакеты данных. В качестве требований в очереди в парикмахерской могут рассматриваться сами клиенты, в потоке больных в приёмном покое больницы – больные и в потоке приходящих на разгрузку в порт судов – сами суда.

Системы обслуживания определяются числом приборов и бывают одноканальные и многоканальные (одна или несколько колонок на бензозаправке и т.д.). Многоканальные системы могут состоять из разнотипных приборов.

Системы бывают полнодоступные и неполнодоступные (обслуживающие приборы или каналы доступны любому требованию – это полнодоступное включение). Полно-доступность и неполнодоступность иллюстрируется рис.В.2. Если использовать аналогии с телефонной связью, то, например, линия «а» доступна абонентам А и В, линия «с» доступна абонентам А и Д, а линия «е» доступна абонентам А, В, С, Д, т.е. всем абонентам.

 

 

 

Рис.В.2. Полнодоступное и неполнодоступное включение.

 

Важным фактором, определяющим работу системы массового обслуживания, является способ обслуживания. Различают способы - в порядке поступления (FIFO), в обратном порядке (LIFO), случайным образом, обслуживание по приоритетам и ряд других. Возможно объединение очередей, взаимодействие очередей и т.д.

Способ обслуживания тесно связан с  поведением клиента – отказ становиться в очередь, использование клиентом априорной информации, уход из очереди до начала обслуживания (соглашение между клиентами) и т.д.

Обозначенный на рис.В.1 выходящий поток, как элемент системы массового обслуживания важен, так как сам может быть входящим потоком для другой системы. Характеристики выходящего потока зависят от характеристик входящего потока и времени обслуживания (если в парик-махерской два мастера с разной производительностью, то это будет влиять и на входящий и на выходящий поток). Анализ выходящего потока позволяет найти характеристики обслуживающих приборов.

В заключение подчеркнем еще раз, что под качеством обслуживания в теории массового обслуживания понимается не то, как хорошо выполнено обслуживание (бритьё, качество ремонта и др.), а как хорошо организовано обслуживание, насколько полно загружены приборы, не создаётся ли большая очередь, велик ли уход не обслуженных требований.

 

Потоки событий.

1.1. Основные определения.

Поток событий – последовательность событий, происхо-дящих одно за другим в случайные моменты времени. Графически поток можно отобразить так, как показано на рис.1.1, где на оси времени отмечено начало наблюдения 0 и моменты наступления событий ,  

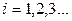
Рис.1.1. Графическое отображение потока событий

Потоки бывают однородными и неоднородными (просто самолёты или самолёты по маркам). Обычно используют однородные потоки.

Регулярный поток – события следуют одно за другим через строго определенные промежутки времени.

  Рис.1.2. Поток событий при независимых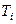

Рассмотрим поток событий, представленный на рис.1.2, где Т₁, Т₂… - случайные интервалы времени (случайные величины), независимые между собой. Такой поток называется потоком Пальма или потоком с ограниченным после-действием.

Поток называется ординарным, если для малого Δt выполняется условие:

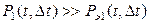                                 ,                  (1.1)

где 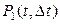 - вероятность того, что за Δt произойдёт одно собы-тие и  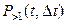- вероятность того, что за Δt произойдёт более одного события.

Таким образом, поток можно считать ординарным, если за малый промежуток времени может произойти не более одного события (или ни одного события, вероятность чего обозначим ).

Для любого Δt очевидно справедливо:

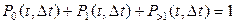                        ,              (1.2)

 т.к. составляющие формулы (1.2) определяют полную группу несовместных событий.

Для ординарного потока:

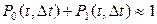                               ,                       (1.3)  

потому что 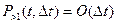, где 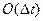 - величина, порядок малос-ти которой выше чем Δt, т. е.:

                                     .                          (1.4)

В качестве примера ординарного потока можно привести ситуацию на автостраде, когда машины пересекают линию «Стоп», даже при многорядном движении. Пример неординарного потока – поток пассажиров, прибывающих в лифте на данный этаж.

Стационарный поток определяется следующим образом. Для стационарного потока вероятность появления некоторого числа событий за интервал τ, зависит только от τ (длины интервала) и не зависит от расположения τ на оси t.

 Регулярный поток и поток Пальма с одинаково распределёнными интервалами T_i являются стационарными потоками.

Возьмём ординарный поток. Среднее число событий, произошедших за время Δt (вычисляется по формуле математического ожидания):

.

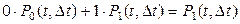Если существует предел

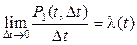                                  ,                        (1.5)  

то 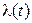 называется интенсивностью ординарного потока (раз-мерность [1/ t]). Для стационарного потока:  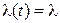- число со-бытий в единицу времени.