Пусть дан стационарный поток Пальма (см. рис.1.3). Все случайные интервалы времени между событиями независимы и имеют одинаковую функцию распределения F(t), которой соответствует плотность вероятности w(t). Здесь в соответствии с принятыми в теории вероятностей правилами записи формул, если случайная величина обозначена большой буквой Т, то аргумент плотности вероятности этой случайной величины обозначается малой буквой t. Это не должно приводить к путанице в обозначениях и ни в коем случае не означает, что w(t) рассматривается как функция текущего времени.
На ось времени случайным образом «падает» точка S, и её положение никак не связано с моментами появления событий. Требуется найти закон распределения того участка T * , на который упала точка (см. рис.1.3).
Описанная модельная ситуация возникает, когда пассажир (точка S) приходит на остановку, а автобус уже ушёл
(предполагается, что поток автобусов – стационарный поток Пальма).

Рис.1.3. Интервал времени, на который падает точка.
Закон распределения 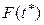 интервала T*, когда пассажир стоит на остановке, отличается от F(t). Упрощенное объяснение этого факта можно представить следующим образом (см. рис.1.4).
интервала T*, когда пассажир стоит на остановке, отличается от F(t). Упрощенное объяснение этого факта можно представить следующим образом (см. рис.1.4).

Рис.1.4. К определению закона распределения 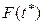
Пусть T принимает два значения с вероятностью 0,5: t1=0,8 и t2=0,2. На остановку приходит пассажир. Более вероятно, что он попадёт на участок длины 0,8. Хотя в среднем число интервалов t1 и t2 одинаково, но t1 в четыре раза длиннее t2. Поэтому вероятность попадания в отрезок длиной 0,8 в четыре раза больше вероятности попадания в отрезок 0,2. Получается, что эти вероятности равны соответственно 0,8 и 0,2. Итак, закон распределения, на который упала точка, отличается от априорного.
Найдём в общем виде плотность w*(t) того интервала T*, на который случайным образом упала точка. Возьмём интервал (t , t+dt). Тогда:

- вероятность того, что S попадёт на интервал, длина которого заключена в промежутке (t , t + dt). Эту вероятность можно определить как отношение суммарной длины таких промежутков на очень большом интервале к длине этого большого интервала. Пусть общее число промежутков (больших и маленьких) на большом интервале равно N .
Среднее число промежутков, длина которых лежит в интервале (t , t + dt), по закону больших чисел равно  , где
, где 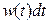 - вероятность наличия любого интервала длиной из промежутка (t , t + dt) среди всех N интервалов. Средняя длина такого интервала -
- вероятность наличия любого интервала длиной из промежутка (t , t + dt) среди всех N интервалов. Средняя длина такого интервала - 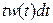 . Средняя суммарная длина таких промежутков -
. Средняя суммарная длина таких промежутков - 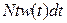 . Средняя общая длина большого интервала -
. Средняя общая длина большого интервала - 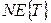 , где
, где 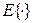 - символ усреднения. При известной плотности w(t) среднее Е{ T } записывается в виде
- символ усреднения. При известной плотности w(t) среднее Е{ T } записывается в виде
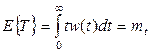 . (1.6)
. (1.6)
( 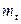 - еще одно обозначение среднего).
- еще одно обозначение среднего).
Следовательно:
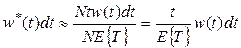 . (1.7)
. (1.7)
При 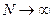 :
:
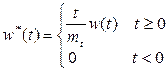 . (1.8)
. (1.8)
Как следует из (1.8) 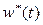 обладает всеми свойствами плотности вероятности. Чтобы найти среднее и дисперсию случайной величины T* целесообразно использовать аппарат характеристических функций.
обладает всеми свойствами плотности вероятности. Чтобы найти среднее и дисперсию случайной величины T* целесообразно использовать аппарат характеристических функций.
По определению характеристическая функция g ( x ) определяется как:
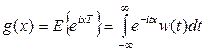 (1.9)
(1.9)
и представляет собой прямое преобразование Фурье плотности вероятности.
Характеристическая функция безразмерна, а перемен-ная x имеет размерность обратную размерности случайной величины T. Соответственно плотность вероятности по известной характеристической функции может быть найдена с помощью обратного преобразования Фурье
 . (1.10)
. (1.10)
Свойства характеристической функции:
1) Если Ti независимые случайные величины и  , то
, то  .
.
Если все Ti распределены одинаково, то 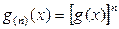
2) 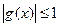
3) g(x) используется для вычисления моментов:
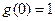 ,
,
 , (1.11)
, (1.11)
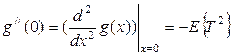 . (1.12)
. (1.12)
Поэтому
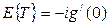 , (1.13)
, (1.13)
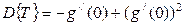 , (1.14)
, (1.14)
где 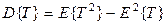 - дисперсия (второй центральный момент) случайной величины Т. Заметим здесь, что через производные более высокого порядка от характеристической функции можно соответственно найти моменты распределения случайной величины более высоких порядков.
- дисперсия (второй центральный момент) случайной величины Т. Заметим здесь, что через производные более высокого порядка от характеристической функции можно соответственно найти моменты распределения случайной величины более высоких порядков.
4) Если случайная величина T имеет характе-ристическую функцию 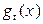 , то случайная величина
, то случайная величина 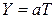 имеет характеристическую функцию в виде
имеет характеристическую функцию в виде
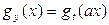 . (1.15)
. (1.15)
Найдём характеристическую функцию случайной величины T* - интервала, на который случайным образом упала точка S.
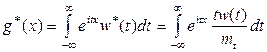
Заметим справедливость соотношения 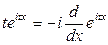 , с учетом которого можно записать
, с учетом которого можно записать
 .
.
С использованием выражения (1.13) ( 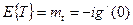 ) для характеристической функции случайной величины T* окончательно получим
) для характеристической функции случайной величины T* окончательно получим
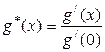 . (1.16)
. (1.16)
На основе выражений (1.16), (1.13) и (1.14) найдём числовые характеристики случайной величины T * . Среднее значение
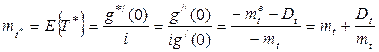 . (1.17)
. (1.17)
Из (1.17) следует, что всегда 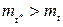 . Лишь в случае регулярного потока событий, когда интервалы становятся неслучайными и, следовательно, Dt=0, получается
. Лишь в случае регулярного потока событий, когда интервалы становятся неслучайными и, следовательно, Dt=0, получается 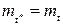 . Таким образом, указание на то, что S попало на какой-то интервал, как бы увеличивает его среднюю длину по сравнению с тем, как его оценивали бы без этого указания.
. Таким образом, указание на то, что S попало на какой-то интервал, как бы увеличивает его среднюю длину по сравнению с тем, как его оценивали бы без этого указания.
Найдём дисперсию случайной величины T * :
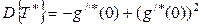 ,
,
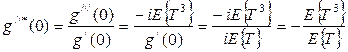 ,
,
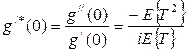 ,
,
 ,
,
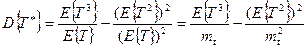 . (1.18)
. (1.18)
Из (1.18) видно, что дисперсия 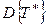 может быть и больше и меньше дисперсии
может быть и больше и меньше дисперсии 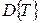 .
.
Дата: 2019-02-02, просмотров: 313.