Рассмотрим элементарный кубик породы в естественных условиях залегания. Это означает отсутствие возмущений в пласте (рис.32). Когда порода находится в естественных условиях залегания, элементарный кубик находится в равновесном состоянии. Массив вышележащих пород давит на кубик, как гидравлический пресс в лаборатории. Напряжение от этой нагрузки стремится сделать элементарный кубик короче и толще, как образец породы в лаборатории. Все окружающие элементарные кубики воспринимают такую же нагрузку, которая также стремится сделать их короче и толще. Эти окружающие кубики, стараясь расшириться, создают боковое давление на наш элементарный кубик. По мере увеличения давления вышележащих пород с глубиной возрастает и боковое давление. Кажущаяся прочность породы остается достаточно высокой, чтобы кубик не разрушился. Со временем давление вышележащих пород и боковое давление увеличиваются настолько, что превышают предел текучести породы. Однако это не произойдет до глубины примерно 80 - 90 тыс. футов.

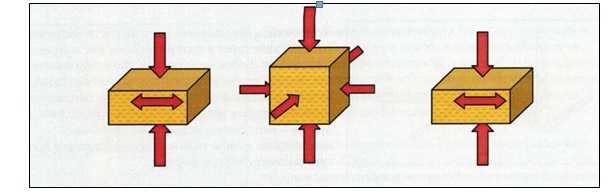
Рис.32 Напряжения в естественных условиях залегания. (В естественных условиях залегания элементарный кубик породы находится в равновесном состоянии. Напряжения от веса вышележащих пород стремятся деформировать породу, окружающую кубик. В результате возникает поперечное или боковое давление, препятствующее деформации кубика. Каждый такой кубик давит на окружающие кубики и испытывает давление с их стороны).

Напряжения на стенке скважины

Наш элементарный кубик породы чувствовал себя превосходно в естественных условиях залегания, в окружении таких же кубиков (рис32). Однако пробурив скважину, мы удалили некоторые окружающие кубики, которые оказывали горизонтальное боковое давление на наш кубик (рис.33).

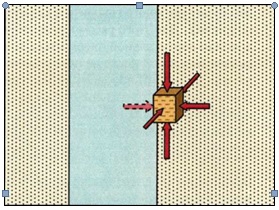
Рис.33 Напряжения на стенке скважины (Пробурив скважину и удалив породу, окружающую наш кубик, мы устранили также боковое давление на этот кубик. Напряжение, действовавшее в удаленном материале, должно быть восполнено).

Напряжение, действовавшее в удаленном материале, должно быть восполнено давлением бурового раствора в скважине и напряжением, действующим со стороны других кубиков, оставшихся на стенке. Если в скважине нет жидкости, то 100 % напряжений передается на стенку как кольцевое напряжение. Кольцевое напряжение является тангенциальным по отношению к стенке скважины. Кольцевое напряжение σ θ  часто называют тангенциальным или окружным напряжением.

Кольцевые напряжения

Мы будет так много говорить о кольцевых напряжениях, что имеет смысл объяснить это понятие подробнее. Для этого рассмотрим сосуд давления, показанный на рис.34. Если разделить сосуд пополам вертикальной плоскостью, то обе половины будут стремиться разойтись. Внутреннее давление, действующее на поперечное сечение каждой половины сосуда, создаст усилие, раздвигающее эти половины. Сила, удерживающая вместе обе половины, обусловлена растягивающим напряжением в стенках сосуда. По величине эта сила равна произведению напряжения на площадь поперечного сечения стенки. Численно она равна силе, стремящейся раздвинуть обе половины. Это кольцевое напряжение остается неизменным по всему периметру сосуда, если не изменяется толщина стенки.

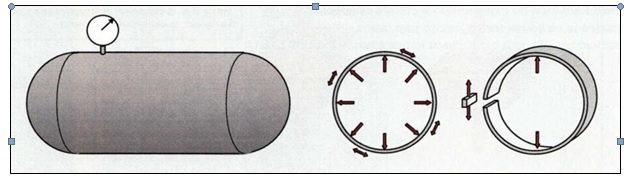
Рис.34 Кольцевые напряжения (Внутреннее давление стремится раздвинуть половины сосуда. В результате в стенках сосуда возникает растягивающее кольцевое напряжение. Если погрузить этот сосуд глубоко в море, в стенках будут действовать сжимающие кольцевые напряжения).

Представим себе, что тот же самый сосуд испытывает давление извне, как при погружении глубоко в море. Теперь наружное давление, действующее на ту же площадь, удерживает обе половины сосуда вместе. Кольцевые напряжения в любом месте сосуда являются сжимающими.

А сейчас посмотрим на сосуд, показанный на рис.35. Когда по оси y действует сила 10 тыс. фунтов, кольцевые напряжения в плоскости x-z равны 1 тыс. фунт/дюйм. Когда по оси x действует сила 5 тыс. фунтов, кольцевые напряжения в плоскости y-z равны 500 фунт/дюйм². Две не равные по величине силы создают кольцевые напряжения разной величины.

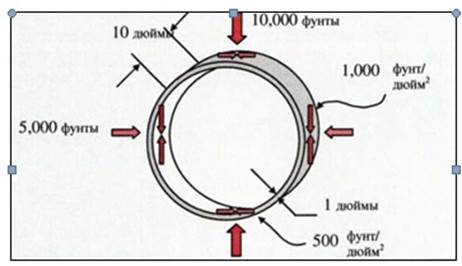
Рис. 35 Кольцевые напряжения

Теперь давайте вернемся к нашему элементарному кубику породы, находящемуся в естественных условиях залегания. Если ствол скважины проходит рядом с этим кубиком, и с одной стороны удалена порода, создающая боковое давление, то недостающие напряжения восполняются кольцевыми напряжениями. Можно посмотреть на эту ситуацию и таким образом, что теперь поле напряжений должно обойти вокруг скважины (рис.36).

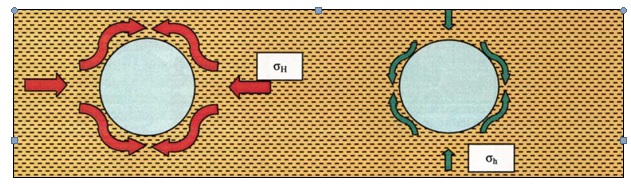
Рис.36 Распределениеинапряжений вокруг ствола скважины (Поскольку в процессе бурения удаляется порода, происходит перераспределение напряжений и возникают кольцевые напряжения).

Если скважина вертикальная, и нет тектонических напряжений, то горизонтальные напряжения (σH и σh) равны, и кольцевые напряжения равномерно распределены вокруг ствола скважины (рис. 37А).

Поскольку тектонические напряжения в той или иной степени существуют везде, то при любом распределении напряжений горизонтальные напряжения будут больше в одном направлении, чем в остальных. Наибольшие горизонтальные напряжения σH должны обойти скважину, как кольцевые напряжения. Это же относится и к наименьшим горизонтальным напряжениям σh. В результате возникают кольцевые напряжения, которые имеют максимальное значение на направлениях, отстоящих на 90° и 270° от направления действия наибольших главных горизонтальных напряжений (рис. 37В).

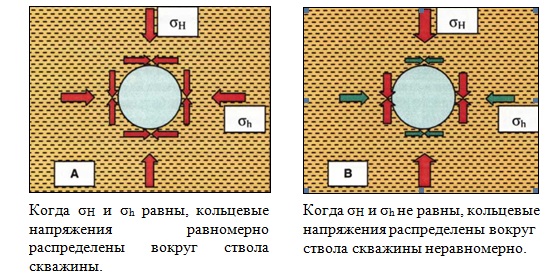
Рис. 37 Кольцевые напряжения на стенках скважины

Посмотрим на скважину, изображенную на рис.38. Принимаем, что тектонические напряжения равны (о"н = 0"ь), тогда кольцевые напряжения на стенках скважины будут распределены равномерно по всей окружности сечения ствола, как показано на рис. 37А. Однако на горизонтальном участке ствола вертикальные напряжения от веса вышележащих пород будут больше действующих горизонтальных напряжений. В результате кольцевые напряжения будут иметь максимальное значение на боковых стенках, и наименьшие значения на верхней и нижней стенках (рис. 37В). Если плотность бурового раствора недостаточно велика, стенки обрушатся в скважину.

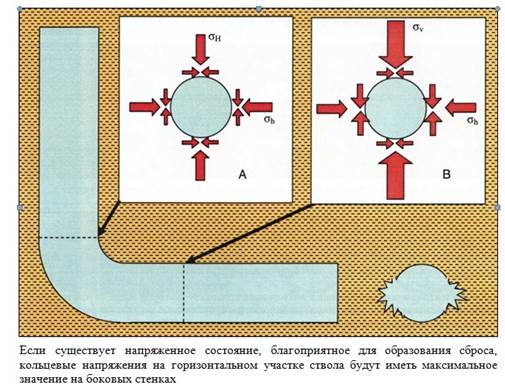
Рис. 38 Анизатропное распределение напряжений

Вероятнее всего, большие разности напряжений будут встречаться на небольших глубинах. Это объясняется тем, что на глубине породы становятся более пластичными из-за более высокого бокового давления. Пластичные породы деформируются до выравнивания напряжений. Этот феномен называется "правило Гейма"3. В горных районах, где высоки тектонические напряжения, кольцевые напряжения могут быть в три раза больше в одном направлении, чем в другом, особенно у поверхности. На очень больших глубинах напряжения почти выравниваются, даже в горных районах.

Кольцевые напряжения отличаются не только в разных точках на стенке скважины, но и с удалением от стенки в пласт. Кольцевые напряжения имеют максимальное значение на стенке и уменьшаются до нуля на расстоянии примерно трех радиусов от стенки скважины (рис.39).

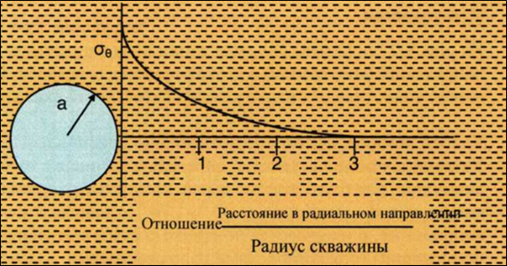
Рис. 39 Изменение кольцевых напряжений с удалением от стенки скважины

Нас интересуют наибольшие и наименьшие кольцевые напряжения (о"е) на стенке скважины. Эти напряжения можно найти по уравнению Кирша. Однако для нашего рассмотрения на уровне концепций лучше подходит графический метод, представленный Геком и Брауном (Hoek & Brown).