Трехосное напряженное состояние породы на стенках скважины (рис.45) характеризуется следующими компонентами:

• σ_z (осевое напряжение)

• σ_r (радиальное напряжение)

• σ_θ (тангенциальное или кольцевое напряжение)

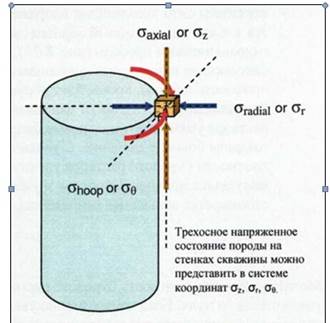
Рис.45 Трехосное напряженное состояние породы на стенках

Порода вываливается из стенок тогда, когда комбинация из любых двух этих напряжений превышает определенный предел.

Два любых взаимно ортогональных напряжения создают касательное напряжение в плоскости, в которой действуют эти напряжения. Если касательное напряжение превысит предел прочности породы, она разрушается и обрушивается в скважину.

Круги напряжений (теория двойного угла)

Для представления напряжений в горной породе, действующих в плоскости, расположенной под любым углом относительно направления максимальных напряжений, часто используют круги напряжений (круги Мора). Этот метод полезен, когда мы знаем напряжения в определенном направлении и хотим знать напряжения в каком-то другом направлении. Кроме того, он полезен для определения главных напряжений и максимальных касательных напряжений.

Большинству инженеров и членов буровых бригад никогда не придется работать с кругами напряжений. Тем не менее, здесь предлагается краткое объяснение, поскольку огибающая предельных кругов напряжений часто используется для прогнозирования интервала допустимых значений плотности бурового раствора. Этот графический подход, проиллюстрированный на рис.46, разработал немецкий инженер Отто Мор (1835 -1918 гг.).

Круги напряжений - графический метод представления главных напряжений и максимальных касательных напряжений в точке массива напряженной горной породы. Ортогональные напряжения в точке представлены в координатах σ, τ. Точки А и В представляют наибольшее и наименьшее напряжения на некоторой поверхности.

Главные напряжения существуют там, где касательные напряжения равны нулю. Наибольшее касательное напряжение численно равно радиусу круга.

Известные напряжения в элементарном кубике представлены на графике в координатах σ, τ. Фундаментальная концепция кругов напряжений заключается в том, что каждая точка окружности характеризует напряженное состояние в воображаемой плоскости, проходящей через породу под некоторым углом θ относительно плоскости, в которой действуют главные напряжения (главной плоскости).

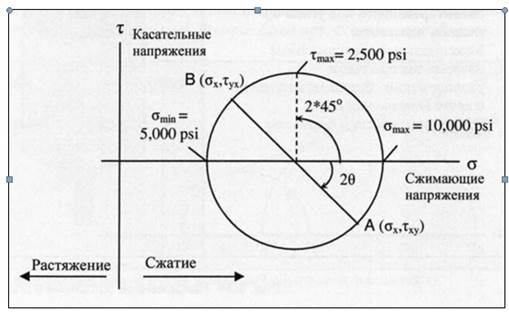
Рис. 46 Круг напряжений (Примечание: чтобы получить круг, все углы нужно удвоить)

Например, на рис. 46 показано напряженное состояние образца породы, изображенного на рис.47. Допустим, что мы хотим пробурить скважину через образец, изображенный на рис.47, под некоторым углом. Напряженное состояние любого элементарного кубика на плоскости, расположенной под этим углом, показано в правом верхнем углу. Точки А и В характеризуют наибольшее и наименьшее сжимающие напряжения в образце до проводки скважины.

Главные напряжения в образце равны 10 тыс. фунт/дюйм² и 5 тыс. фунт/дюйм². Напомним, что в главных плоскостях касательные напряжения всегда равны нулю. Поэтому все точки, где действуют главные напряжения, лежат на оси σ. Максимальное касательное напряжение численно равно радиусу круга и действует в плоскости, расположенной под углом 45° относительно главной плоскости. В данном случае максимальное касательное напряжение равно 2,5 тыс. фунт/дюйм².

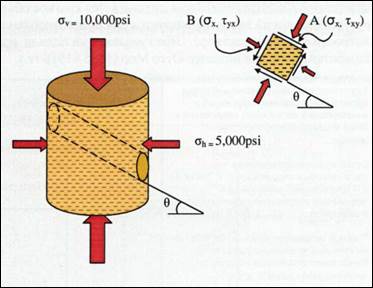
Рис.47 Напряженное состояние в плоскости

Главные плоскости в этом образце ортогональны σv и σh. Справа показано напряженное состояние выделенного элемента, ориентированного под углом θ к главной плоскости. Максимальные и минимальные напряжения при таком расположении образца можно найти в круге напряжений по тригонометрическим формулам.

По кругу напряжений видно, что при увеличении разности между наибольшим и наименьшим главными напряжениями возрастает максимальное касательное напряжение. Максимальное касательное напряжение всегда равно половине разности между максимальным и минимальным напряжениями (радиус круга напряжений). Это важно отметить, потому что обрушение породы со стенок скважины обычно происходит из-за чрезмерных касательных напряжений!

Касательное напряжение всегда равно нулю на поверхности, где действуют главные напряжения.

Касательные напряжения не могут существовать на открытых поверхностях, находящихся в контакте с жидкостью, таких как стенки скважины. Поэтому после проводки скважины одна главная плоскость будет ориентирована параллельно траектории скважины, а другая будет ей ортогональна. Можно начертить новый круг напряжений для прогнозирования максимального касательного напряжения в таких условиях.