ПРОБЛЕМЫ НАДЕЖНОСТИ И ЕЕ ЗНАЧЕНИЕ ДЛЯ СОВРЕМЕННОЙ ТЕХНИКИ

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

ПРОБЛЕМЫ НАДЕЖНОСТИ И ЕЕ ЗНАЧЕНИЕ ДЛЯ СОВРЕМЕННОЙ ТЕХНИКИ

Надежность является важнейшим технико-экономическим показателем качества любого технического устройства, в частности электрической машины, определяет ее способность безотказно работать с неизменными техническими характеристиками в течение заданного промежутка времени при определенных условиях эксплуатации.

С древнейших времен при изготовлении изделий для обеспечения надежности закладывался определенный запас прочности, чем и гарантировалась долговечность работы. Однако это приводило к излишним затратам материалов, увеличению габаритов, массы и стоимости изделий. С развитием электрификации задачи обеспечения надежного снабжения объектов электроэнергией решались, в основном, путем резервирования (параллельная работа трансформаторов и электрических генераторов, объединение разрозненных энергетических объектов в единую энергетическую систему и т.д.). Новые проблемы надежности возникли с развитием авиации, дальнего плавания, ракетной и космической техники. Первоначально задачи надежности и здесь решались традиционными методами. Однако этот путь скоро стал малоэффективным, т.к. приводил к резкому увеличению габаритов и массы, что для авиационной и космической техники является неприемлемым. Поэтому для повышения надежности стали использоваться новые методы, основанные на теории вероятностей и математической статистики.

Теория надежности ЭМ в ее современном виде стала разрабатываться сравнительно недавно – около 30 лет назад. На протяжении нескольких предшествующих десятилетий электромашиностроение развивалось в направлении повышения использования машин, увеличения нагрузок активных материалов и снижения массы машины на единицу мощности. Параллельно с этим разрабатывались и внедрялись новые типы активных, конструкционных и изоляционных материалов, улучшались вентиляция, появились более интенсивные методы охлаждения машин. Однако запас прочности, а вместе с тем и устойчивость к перегрузкам постепенно снижались. В результате наметилась тенденция общего снижения надежности ЭM. Первые работы, в которых было указано на недостаточный уровень надежности ЭМ, были опубликованы в 1961 г. В них на примере работы ряда металлургических предприятий давался экономический анализ материально-технического ущерба в промышленности из-за отказов или недостаточной надежности электрических двигателей. Потребовалось определенное время, прежде чем стало общепризнанным, что повышение использования активных и конструктивных материалов целесообразно лишь до тех пор, пока эта тенденция не приводит к снижению надежности ЭМ.

Проблема надежности технических систем за последние два-три десятилетия резко обострилась, что объясняется следующими объективными причинами:

1. Резким увеличением сложности технических систем, включающих сотни тысяч и даже миллионы отдельных узлов и элементов

2. Экстремальность условий, в которых эксплуатируются изделия (высокие скорости, значительные ускорения, высокие температуры и давления, вибрация, повышенная радиация и т.д.)

3. Интенсивностью режимов работы системы или отдельных узлов (при высоких температуре, частотах вращения, давлениях, плотности тока и т.д.)

4. Повышением требований к качеству работ (высокая точность, эффективность и т.д.)

5. Увеличением ответственности функций, выполняемых системой, высокой экономической и технической ценой отказа

6. Полной или частичной автоматизацией и, как следствие, исключением непосредственного контроля человеком функционирования системы и ее элементов

ПОКАЗАТЕЛИ НАДЕЖНОСТИ

Показатели надежности можно разбить на две группы, характеризующие невосстанавливаемые (обмотки ротора и статора ЭМ, щетки, подшипники) и восстанавливаемые (подшипниковый и коллекторно–щеточные узлы, пускорегулирующая аппаратура) объекты.

К числу широко применяемых количественных характеристик надежности невосстанавливаемых объектов относятся: вероятности безотказной работы Р(t) и отказа Q(t), частота отказов а(t), интенсивность отказов l(t), средняя наработка до первого отказа Т_ср.

P,Q

Вероятность безотказной работы (ВБР) – вероятность того, что при определенных условиях эксплуатации в заданном интервале времени не произойдет ни одного отказа. Вероятность Р(t) функция убывающая (рис. 6.1), причем 0 £ Р(t) £ 1; P(0) = 1; P(¥) = 0.

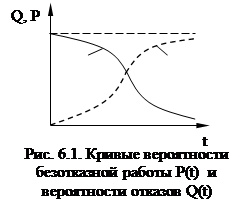ВБР по статическим данным об отказах оценивается выражением

(6.1)

где Р^*(t) – статическая оценка ВБР, N₀ – число изделий в начале испытаний, n(t) – число отказавших изделий за время t.

При большом числе изделий N₀ статическая оценка P^*(t) практически совпадает с вероятностью P(t).

Вероятность отказа Q(t) – вероятность того, что при определенных условиях эксплуатации в заданном интервале времени произойдет хотя бы один отказ. Отказ и безотказная работа – события противоположные и не совместимые:

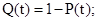
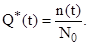(6.2)

Частота отказов а(t) – есть отношение числа отказавших изделий в единицу времени к первоначальному числу испытываемых изделий:

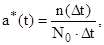(6.3)

где n(Dt) – число отказавших изделий в интервале времени Dt.

Частота отказов или плотность вероятности отказов f(t) может быть определена как производная по времени вероятности отказов

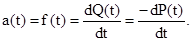(6.4)

Интенсивность отказов l(t) – условная плотность вероятности возникновения отказа, которая определяется как отношение числа отказавших изделий n(Dt) в единицу времени к среднему числу изделий исправно работающих в данный отрезок времени

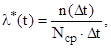(6.5)

где 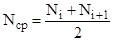– среднее число изделий, исправно работающих в интервале Dt; N_i, N_i₊₁ – соответственно числа изделий, исправно работающих в начале и конце интервала Dt, N_i³N_i₊₁.

Интенсивность отказов l(t) – является также отношение частоты отказов к ВБР

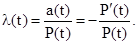(6.6)

Вероятность безотказной работы и интенсивность отказов связаны выражением

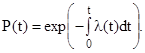(6.7)

Обычно интенсивность отказов меняется во времени. Лишь в случае экспоненциального закона распределения отказов интенсивность отказов .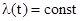

Средней наработкой до отказа Т_ср – математическое ожидание наработки объекта до первого отказа. Математическое ожидание Р_ср вычисляется следующим образом

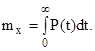(6.8)

По статическим данным об отказах средняя наработка до первого отказа вычисляется по формуле

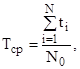(6.9)

где t_i – время безотказной работы i–го образца; N₀ – число испытуемых изделий.

Для определения Т_ср необходимо знать время безотказной работы всех испытуемых изделий. Иногда это не представляется возможным и поэтому пользоваться формулой 6.9 неудобно. Имея данные о количестве вышедших из строя элементов n_i в каждом i–ом интервале времени, среднюю наработку до первого отказа можно определить из уравнения

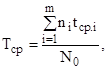(6.10)

где m – количество интервалов длительностью Dt. Значение t_cp_._i и m находятся по следующим зависимостям

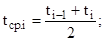
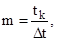(6.11)

где t_i_-1, t_i – время начала и окончания i–го интервала; t_k – время в течение которого вышли из строя все изделия.

Пример: Проводятся ресурсные испытания.

Установлено 400 машин. Через 3000 ч работы отказало 200 машин. Испытания продолжались и через 100 ч отказало еще 100 машин. Определить Р^*(3000), Q^*(3000), P^*(3100), Q^*(3100), P^*(3050), l^*(3050), a^*(3050).

В соответствии с формулами 17.1, 17.2 определим вероятность безотказной работы и вероятность отказа за 3000 и 3100 ч.

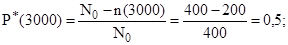
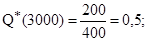
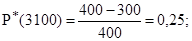
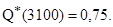
Среднее число исправно работающих машин в интервале от 3000 до 3100 ч

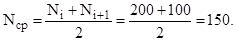
Число отказавших машин за 3050 ч и Р^*(3050) равны

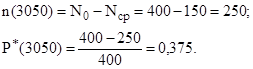
Частота и интенсивность отказов определяются по формулам 6.3 и 6.5

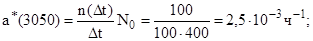
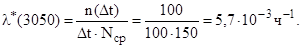
Таблица 6.1

А/C₀	0,014	0,028	0,056	0,084	0,11	0,17	0,28	0,42	0,56
e	0,19	0,22	0,26	0,28	0,30	0,34	0,38	0,42	0,44
Y	2,30	1,99	1,71	1,55	1,45	1,31	1,15	1,04	1,00

Для промежуточных значений A/C₀ применяют линейную интерполяцию. При A/C₀< 0,19 приведенная нагрузка Q = R. При отсутствии аксиальной нагрузки и горизонтальном расположении вала осевое магнитное притяжение в расчете не учитывается, а при вертикальном расположении вала А = 1,15G + F_c + 0,1R, где F_c = 9,81m/2 – сила тяжести соединительного устройства (упругой муфты или шкива), кг.

Необходимая динамическая грузоподъемность:

шарикоподшипника 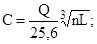(6.13)

роликоподшипника 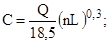(6.14)

где L – расчетный срок службы подшипника, ч (обычно принимается 12 000 ч); n – наибольшая рабочая частота вращения машины, об/мин.

Из справочников или ГОСТов, указанных выше, выбирают подшипник, соответствующей серии, у которого внутренний диаметр равен диаметру шейки вала, а динамическая грузоподъемность не менее значений, вычисленных по формулам 6.13 и 6.14.

В большинстве своем расчет подшипников используется функция Вейбулла, которая с наибольшим приближением аппроксимирует закон распределения долговечности подшипников

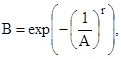
где В – доля из общего числа подшипников, для которых обеспечивается заданная долговечность; А, r – параметры закона, зависящие от отношения средней долговечности h_cp к гарантированной h_г.

Установлено, что для большинства типов подшипников отклонение h_cp/h_г= 4,08, исходя из чего А_4,08= 5,38d/h; r_4,08= 1,34, где h – необходимый ресурс в течение которого гарантируется безаварийная работа; d – условная расчетная долговечность.

Уравнение Вейбулла в этом случае принимает вид

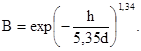
Рассмотрим ещё один метод определения надежности подшипниковых узлов ЭМ. Здесь с учетом различных причин отказов надежность оценивается вероятностью безотказной работы также с помощью распределения Вейбулла

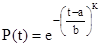при t>a;

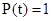при t£a,

где параметр сдвига а характеризует зону, в которой вероятность отказа практически равна нулю. Параметры а, b, к находятся экспериментально по формулам

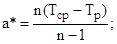
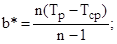
где а^*, b^* - оценки параметров а и b; n – объем выборки; Т_ср– наработки до первого отказа; Т_р – средний ресурс.

ПРОБЛЕМЫ НАДЕЖНОСТИ И ЕЕ ЗНАЧЕНИЕ ДЛЯ СОВРЕМЕННОЙ ТЕХНИКИ

4. Повышением требований к качеству работ (высокая точность, эффективность и т.д.)

Дата: 2018-12-28, просмотров: 294.

12 3 4 5 Следующая ⇒