Перечень рекомендуемых нормативных правовых актов, учебных изданий (основных и дополнительных источников), периодических изданий, Интернет-ресурсов и др.
3.2.1. Основные источники:
1. Баврин, И. И. Математический анализ : учебник и практикум для СПО / И. И. Баврин. - 2-е изд., испр. и доп. - М. : Издательство Юрайт, 2016. - 327 с. - (Серия : Профессиональное образование). - ISBN 978-5-9916-6247-5. http://www.biblio-online.ru/book/A82F8297-618B-4E9D-BEFB-D36445F4CB46
2. Богомолов, Н. В. Практические занятия по математике : учебное пособие для СПО / Н. В. Богомолов. - 11-е изд., перераб. и доп. - М. : Издательство Юрайт, 2016. - 495 с. - (Серия : Профессиональное образование). - ISBN 978-5-9916-6107-2. http://www.biblio-online.ru/book/C712F93E-9719-49A8-8D82-624B5EBBFBEE
3. Высшая математика : учебник и практикум для СПО / М. Б. Хрипунова [и др.] ; под общ. ред. М. Б. Хрипуновой, И. И. Цыганок. - М. : Издательство Юрайт, 2017. - 472 с. - (Серия : Профессиональное образование). - ISBN 978-5-534-01497-6. http://www.biblio-online.ru/book/79006A6A-C94E-438B-AADE-B32FC5E081D5
3.2.2. Дополнительные источники:
1. Дорофеева, А. В. Математика. Сборник задач : учеб.-практ. пособие для СПО / А. В. Дорофеева. - 2-е изд. - М. : Издательство Юрайт, 2017. - 176 с. - (Серия : Профессиональное образование). - ISBN 978-5-534-03712-8. http://www.biblio-online.ru/book/F0561609-26AD-401A-A2FA-7222FCECB71C
2. Красс, М. С. Математика в экономике. Базовый курс : учебник для СПО / М. С. Красс. - 2-е изд., испр. и доп. - М. : Издательство Юрайт, 2016. - 471 с. - (Серия : Профессиональное образование). - ISBN 978-5-9916-9134-5. http://www.biblio-online.ru/book/6EDAFAE8-1931-466B-B9D3-926EB7B15094
3. Павлюченко, Ю. В. Математика : учебник и практикум для СПО / Ю. В. Павлюченко, Н. Ш. Хассан ; под общ. ред. Ю. В. Павлюченко. - 4-е изд., перераб. и доп. - М. : Издательство Юрайт, 2017. - 238 с. - (Серия : Профессиональное образование). - ISBN 978-5-534-01261-3. http://www.biblio-online.ru/book/773FAB0F-0EF8-4626-945D-6A8208474676
4. Шевалдина, О. Я. Математика в экономике : учебное пособие для СПО / О. Я. Шевалдина. - М. : Издательство Юрайт, 2017. - 194 с. - (Серия : Профессиональное образование). - ISBN 978-5-534-04877-3. http://www.biblio-online.ru/book/940F47B0-6072-42D3-A5A3-380444AB40B3
3.2.3. Интернет-ресурсы:
1. Единое окно доступа к образовательным ресурсам. - URL: http://
window.edu.ru
2. Единая коллекция цифровых образовательных ресурсов. - URL: http://
school-collection.edu.ru/
3. Прикладная математика. Справочник математических формул. Примеры и задачи с решениями. http://pm298.eto.tom.ru/
4. Архив учебных материалов по математике. URL:http://www.rusedu.ru/
3.3. Организация образовательного процесса
Изучение дисциплины «Математика» включает теоретические, практические, комбинированные занятия, занятия применения знаний и умений, а также внеаудиторную самостоятельную работу.
В процессе проведения аудиторных занятий применяются следующие формы организации учебной деятельности:
- фронтальная (предполагает работу всех студентов над одним и тем же содержанием, работу преподавателя со всей группой в едином темпе, с общими заданиями);
- групповая (при решении задач повышенного уровня сложности в малых группах);
- парная (предполагает либо взаимодействие двух студентов в процессе анализа и обсуждения задачи, осуществления взаимообучения и взаимоконтроля; либо взаимодействие педагога и студента);
- индивидуальная (предполагает самостоятельный выбор студентом индивидуального маршрута изучения учебного материала в рамках заданной темы, каждый студент работает в своем темпе над посильными ему заданиями).
При проведении занятий используются
активные методы обучения:
- фронтальная работа (Исследование функции на монотонность, экстремумы, выпуклость, Полное исследование функции и построение графика, Вычисление табличных интегралов, Решение прикладных задач в области профессиональной деятельности, Решение систем линейных уравнений)
и интерактивные методы:
- работа в малых группах (Вычисление производных высших порядков. Вычисление пределов с помощью производных, Вычисление определенных интегралов, Действия над событиями. Теоремы сложения и умножения вероятностей).
Аудиторная самостоятельная работа выполняется на занятиях.
В рамках внеаудиторной самостоятельной работы обучающимся предлагается:
- решение задач по темам – предполагает самостоятельное выполнение типовых задач разных уровней сложности с целью отработки умений применения изученных правил и алгоритмов, при этом все студенты работают над одним и тем же набором задач.
4. Контроль и оценка результатов Освоения дисциплины
Контроль и оценка результатов освоения дисциплины осуществляется преподавателем в процессе проведения практических занятий, устных и письменных опросов, тестирования, выполнения обучающимися индивидуальных заданий, самостоятельной работы, а также при защите домашней контрольной работы (для обучающихся по заочной форме).
| Результаты обучения (освоенные умения, усвоенные знания) | Основные показатели оценки результатов | Формы и методы контроля и оценки результатов обучения |
| уметь решать прикладные задачи в области профессиональной деятельности | - использование математических методов при решении задач с практическим содержанием | Оценка по результатам наблюдения за деятельностью обучающихся при выполнении работ на практических занятиях. Оценка выполнения задания самостоятельной работы |
| значение математики в профессиональной деятельности и при освоении профессиональной образовательной программы | - использование математических методов при решении задач с практическим содержанием | Оценка по результатам наблюдения за деятельностью обучающихся при выполнении работ на практических занятиях. Оценка выполнения задания самостоятельной работы |
| знать основные математические методы решения прикладных задач в области профессиональной деятельности | - использование подходящих математических методов для решения задачи профессиональной направленности | Оценка по результатам наблюдения за деятельностью обучающихся при выполнении работ на практических занятиях. Оценка выполнения задания самостоятельной работы |
| знать основные понятия и методы математического анализа, дискретной математики, линейной алгебры, теории комплексных чисел, теории вероятностей и математической статистики | - формулирование определения матрицы и действий над ними,
- указание способов решения СЛАУ и формулирование их алгоритмов,
- формулирование способов вычисления предела функции, требующей раскрытия неопределенностей типа 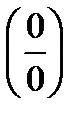 и и 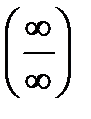 -формулировка понятия множества;
-указание основных операций над множествами,
- формулировка понятия графа и его видов,
- указание способов задания графа,
- формулирование основных комбинаторных объектов и воспроизведение их формул,
- формулирование классической формулы вероятности,
- указание числовых характеристик выборки и воспроизведение их формул
- формулировка определения комплексного числа,
- указание формулы записи комплексного числа в тригонометрической форме
-формулировка понятия множества;
-указание основных операций над множествами,
- формулировка понятия графа и его видов,
- указание способов задания графа,
- формулирование основных комбинаторных объектов и воспроизведение их формул,
- формулирование классической формулы вероятности,
- указание числовых характеристик выборки и воспроизведение их формул
- формулировка определения комплексного числа,
- указание формулы записи комплексного числа в тригонометрической форме
| Оценка по результатам устного, письменного опроса. Оценка в ходе выполнения самостоятельной работы по теме |
| знать основы интегрального и дифференциального исчисления | - формулирование определения производной и воспроизведение формул производных элементарных, сложных функций - формулирование определения неопределенного интеграла и воспроизведение формул, вычисляющих неопределенный интеграл - формулирование формулы Ньютона-Лейбница | Оценка по результатам устного, письменного опроса. Оценка в ходе выполнения самостоятельной работы по теме |
Приложение 1
Примерный перечень вопросов к дифференцированному зачету
1) Определение матрицы. Действия над матрицами.
2) Определитель матрицы 2 и 3 порядка. Свойства определителей.
3) Определение СЛАУ. Формулы Крамера, метод Гаусса и матричный способ решения СЛАУ.
4) Предел функции. Свойства пределов.
5) Методы раскрытия неопределенностей типа 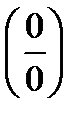 и
и 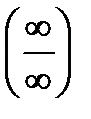 .
.
6) Первый и второй замечательные пределы.
7) Производная функции. Правила дифференцирования. Производные основных элементарных функций.
8) Сложная функция. Правило дифференцирования сложной функции.
9) Производные высших порядков.
10) Определение точки максимума и минимума, экстремумов функции. Необходимое и достаточное условие точки экстремума.
11) Определение возрастания и убывания функции. Достаточное условие возрастания и убывания функции.
12) Определение выпуклости, вогнутости функции, точки перегиба. Условие выпуклости, вогнутости функции. Достаточное условие точки перегиба.
13) Определение асимптоты графика функции. Виды асимптот и их условия.
14) План полного исследования функции.
15) Определение дифференциала функции. Свойства дифференциала.
16) Первообразная функции. Неопределенный интеграл. Свойства неопределенного интеграла.
17) Таблица неопределенных интегралов. Методы вычисления интегралов.
18) Определенный интеграл. Формула Ньютона-Лейбница.
19) Виды событий. Вероятность события. Классическая формула вероятности.
20) Выборочный метод. Числовые характеристики выборки.
Приложение 2
Лист изменений, вносимых в рабочую программу дисциплины
на 20__/ 20__ учебный год
Все изменения рабочей программы рассмотрены и одобрены на заседании ПЦК информационных и естественнонаучных дисциплин
Протокол от «___»________20__г. № _____
Председатель ПЦК М.Е. Куликова
Дата: 2018-12-28, просмотров: 347.