РАБОЧАЯ ПРОГРАММА
Наименование дисциплины Математика
Специальность 38.02.06 Финансы
По программе базовой подготовки
Уровень образования основное общее образование
Квалификация выпускника финансист
Форма обучения очная, заочная курс 2
2018
Рабочая программа дисциплины разработана на основе Федерального государственного образовательного стандарта (далее ФГОС) по специальности среднего профессионального образования (далее СПО) 38.02.06 Финансы.
Разработчик:
Алешкова Т.Н., преподаватель
Рабочая программа рассмотрена и одобрена на заседании предметно-цикловой комиссии (далее ПЦК) информационных и естественнонаучных дисциплин
Протокол от «______» ___________ 201___ г. № _____
Председатель ПЦК ________________ М.Е. Куликова
подпись
СОДЕРЖАНИЕ
| стр. | |
| 1. ПАСПОРТ рабочей ПРОГРАММЫ ДИСЦИПЛИНЫ | 4 |
| 2. СТРУКТУРА и содержание ДИСЦИПЛИНЫ | 6 |
| 3. условия реализации рабочей программы дисциплины | 15 |
| 4. Контроль и оценка результатов Освоения дисциплины | 18 |
| ПРИЛОЖЕНИя | 20 |
ПАСПОРТ рабочей ПРОГРАММЫ ДИСЦИПЛИНЫ
Математика
Область применения программы
Рабочая программа дисциплины является частью программы подготовки специалистов среднего звена в соответствии с ФГОС по специальности СПО 38.02.06 Финансы базового уровня.
СТРУКТУРА И СОДЕРЖАНИЕ ДИСЦИПЛИНЫ
2.1. Объем дисциплины и виды учебной работы по очной форме обучения
| Вид учебной работы | Объем часов |
| Максимальная учебная нагрузка (всего) | 76 |
| Обязательная аудиторная учебная нагрузка (всего) | 70 |
| в том числе: | |
| теоретическое обучение | 32 |
| практические занятия | 38 |
| Внеаудиторная самостоятельная работа обучающихся (всего) | 6 |
| в том числе: | |
| решение задач | 6 |
| Промежуточная аттестация в форме | |
Дифференцированного зачета
2.2. Объем дисциплины и виды учебной работы по заочной форме обучения
| Вид учебной работы | Объем часов |
| Максимальная учебная нагрузка (всего) | 76 |
| Обязательная аудиторная учебная нагрузка (всего) | 16 |
| в том числе: | |
| теоретическое обучение | 6 |
| практические занятия | 10 |
| Внеаудиторная самостоятельная работа обучающихся (всего) (в т.ч. домашняя контрольная работа) | 60 |
| Промежуточная аттестация в форме дифференцированного зачета | |
.
2.3. Тематический план и содержание дисциплины по очной форме обучения
Математика
| Наименование разделов и тем |
Содержание учебного материала и формы организации деятельности обучающихся | Объем часов | |
| 1 | 2 | 3 | |
|
Раздел 1. Основные понятия и методы математического анализа | 37 | ||
| Тема 1.1. Изучение элементов теории пределов | Содержание учебного материала | Уровень освоения | 9 |
| Предел функции. Теоремы о пределах функций. Два замечательных предела. Бесконечно малые и бесконечно большие функции. Сравнение бесконечно малых и бесконечно больших функций. Понятие непрерывности функции. Непрерывность элементарных функций. Основные свойства непрерывных функций. | 1 | ||
|
Тематика учебных занятий | 8 | ||
|
Теоретическое обучение | 4 | ||
| Предел функции. Методы раскрытия основных неопределенностей. | 2 | ||
| Непрерывность функции. | 2 | ||
|
Практические занятия | 4 | ||
|
Раскрытие основных неопределенностей | 2 | ||
| 2. Применение первого и второго замечательных пределов и бесконечно малых к раскрытию неопределенностей (практическая работа) | 2 | ||
| Внеаудиторная самостоятельная работа обучающихся | 1 | ||
| 1. Решение задач | 1 | ||
| Тема 1.2.Изучение элементов дифференциального исчисления. | Содержание учебного материала | Уровень освоения | 17 |
| Понятие производной. Понятие дифференцируемости функции. Понятие дифференциала функции. Правила дифференцирования суммы, произведения и частного. Производные элементарных функций. Дифференцирование сложной функции. Производные и дифференциалы высших порядков. Исследование функций и построение графиков. | 1 | ||
|
Тематика учебных занятий | 16 | ||
|
Теоретическое обучение | 8 | ||
| 1. Понятие производной функции. Экономический смысл производной. Правила и формулы дифференцирования. | 2 | ||
| 2. Производные высших порядков. Дифференциал функции. Применение производной к вычислению пределов. | 2 | ||
| 3.Монотонность, экстремумы, выпуклость, вогнутость функции. | 2 | ||
| 4. Полное исследование функции и построение графика | 2 | ||
|
Практические занятия | 8 | ||
| 1.Вычисление производных элементарных и сложных функций (практическая работа) | 2 | ||
| 2.Вычисление производных высших порядков. Вычисление пределов с помощью производных (в форме групповой работы) | 2 | ||
| 3. Исследование функции на монотонность, экстремумы, выпуклость (в форме фронтальной работы). | 2 | ||
| 4.Построение графиков функций (в форме фронтальной работы, практическая работа) | 2 | ||
| Внеаудиторная самостоятельная работа обучающихся | 1 | ||
| 1. Решение задач | 1 | ||
|
Тема 1.3 Изучение элементов интегрального исчисления | Содержание учебного материала | Уровень освоения | 11 |
| Первообразная и неопределенный интеграл. Основные свойства неопределенного интеграла. Таблица неопределенных интегралов. Основные методы интегрирования. Определенный интеграл. Свойства определенного интеграла. | 1 | ||
|
Тематика учебных занятий | 10 | ||
|
Теоретическое обучение | 4 | ||
| 1. Неопределенный интеграл и его свойства. | 2 | ||
| 2. Методы интегрирования. | 2 | ||
|
Практические занятия | 6 | ||
| 1.Вычисление табличных интегралов (в форме фронтальной работы) | 2 | ||
| 2.Методы интегрирования (практическая работа) | 2 | ||
| 3.Вычисление определенных интегралов (комбинированное занятие, в форме групповой работы) | 2 | ||
| Внеаудиторная самостоятельная работа обучающихся | 1 | ||
| 1. Решение задач | 1 | ||
|
Тематика учебных занятий | 4 | ||
|
Теоретическое обучение | 2 | ||
| 1.Множество. Операции над множествами. Графы, способы задания графов. | 2 | ||
|
Практические занятия | 2 | ||
| 1.Выполнение операций над множествами (практическая работа) | 2 | ||
|
Тематика учебных занятий | 10 | ||
|
Теоретическое обучение | 4 | ||
| 1.Понятие матрицы. Действия над матрицами. Определители. Вычисление определителей. | 2 | ||
| 2. Обратная матрица. Решение матричных уравнений. | 2 | ||
|
Практические занятия | 6 | ||
| 1.Выполнение действий над матрицами, вычисление определителей. | 2 | ||
| 2. Вычисление определителей и обратной матрицы в программе Excel. | 2 | ||
| 3. Решение прикладных задач в области профессиональной деятельности (в форме фронтальной работы) | 2 | ||
| Внеаудиторная самостоятельная работа обучающихся | 1 | ||
| 1. Решение задач | 1 | ||
| Тема 3.2 Решение систем линейных уравнений | Содержание учебного материала | Уровень освоения | 7 |
| Системы линейных алгебраических уравнений. Методы решения систем линейных уравнений. Однородные системы линейных уравнений. | 1 | ||
|
Тематика учебных занятий | 6 | ||
|
Теоретическое обучение | 2 | ||
| 1.Способы решения системы m линейных уравнений с n неизвестными. | 2 | ||
|
Практические занятия | 4 | ||
| 1.Решение систем линейных уравнений (в форме фронтальной работы, практическая работа) | 2 | ||
| 2.Решение прикладных задач в области профессиональной деятельности (в форме групповой работы) | 2 | ||
| Внеаудиторная самостоятельная работа обучающихся | 1 | ||
| 1. Решение задач | 1 | ||
|
Тематика учебных занятий | 4 | ||
|
Теоретическое обучение | 2 | ||
| 1.Понятие комплексного числа. Формы записи комплексных чисел. Действия с комплексными числами. | 2 | ||
|
Практические занятия | 2 | ||
| 1.Выполнение действий с комплексными числами (практическая работа) | 2 | ||
|
6,5 | |||
| Вероятность события. Классическая формула вероятности. | 1 | ||
|
Тематика учебных занятий | 6 | ||
|
Теоретическое обучение | 2 | ||
| 1.Формулы комбинаторики. Случайное событие, вероятность случайного события. | 2 | ||
|
Практические занятия | 4 | ||
| 1.Решение задач на вычисление вероятностей событий по классической формуле | 2 | ||
| 2. Действия над событиями. Теоремы сложения и умножения вероятностей (в форме групповой работы) | 2 | ||
| Внеаудиторная самостоятельная работа обучающихся | 0,5 | ||
| 1. Решение задач | 0,5 | ||
| Тема 5.2 Изучение элементов математической статистики. | Содержание учебного материала | Уровень освоения |
4,5 |
| Генеральная совокупность и выборка. Числовые характеристики выборки | 1 | ||
|
Тематика учебных занятий | 4 | ||
|
Теоретическое обучение | 2 | ||
| 1. Понятие о выборочном методе, выборочное среднее и выборочная дисперсия. | 2 | ||
|
Практические занятия | 2 | ||
| 1. Вычисление числовых характеристик выборки (практическая работа) | 2 | ||
| Внеаудиторная самостоятельная работа обучающихся | 0,5 | ||
| 1. Решение задач | 0,5 | ||
| Итоговое занятие | Дифференцированный зачет | 2 | |
| Всего: | 76 | ||
Для характеристики уровня освоения учебного материала используются следующие обозначения:
1 – ознакомительный (узнавание ранее изученных объектов, свойств);
2 – репродуктивный (выполнение деятельности по образцу, инструкции или под руководством);
3 – продуктивный (планирование и самостоятельное выполнение деятельности, решение проблемных задач).
2.4. Тематический план и содержание дисциплины по заочной форме обучения
Математика
|
Наименование разделов И тем |
Содержание учебного материала и формы организации деятельности обучающихся |
Объем часов | ||||||||||||||
| 1 | 2 | 3 | ||||||||||||||
|
Раздел 1. Основные понятия и методы математического анализа | 42 | |||||||||||||||
| Тема 1.1. Изучение элементов теории пределов | Содержание учебного материала | Уровень освоения | 14 | |||||||||||||
| Предел функции. Теоремы о пределах функций. Два замечательных предела. Бесконечно малые и бесконечно большие функции. Сравнение бесконечно малых и бесконечно больших функций. Понятие непрерывности функции. Непрерывность элементарных функций. Основные свойства непрерывных функций. | 1 | |||||||||||||||
|
Тематика учебных занятий | 2 | |||||||||||||||
|
Практические занятия | 2 | |||||||||||||||
| Вычисление пределов функций | 2 | |||||||||||||||
| Внеаудиторная самостоятельная работа обучающихся | 12 | |||||||||||||||
| Бесконечно малые и бесконечно большие функции. Сравнение бесконечно малых и бесконечно больших функций. Понятие непрерывности функции. Непрерывность элементарных функций. Основные свойства непрерывных функций. | 12 | |||||||||||||||
| Тема 1.2. Изучение элементов дифференциального исчисления. | Содержание учебного материала | Уровень освоения | 14 | |||||||||||||
| Понятие производной. Понятие дифференцируемости функции. Понятие дифференциала функции. Правила дифференцирования суммы, произведения и частного. Производные элементарных функций. Дифференцирование сложной функции. Производные и дифференциалы высших порядков. Исследование функций и построение графиков. | 1 | |||||||||||||||
|
Тематика учебных занятий | 3 | |||||||||||||||
|
Теоретическое обучение | 1 | |||||||||||||||
| 1. Понятие производной функции. Экономический смысл производной. Правила и формулы дифференцирования. | 1 | |||||||||||||||
|
Практические занятия | 2 | |||||||||||||||
| 1.Вычисление производных элементарных и сложных функций. | 2 | |||||||||||||||
| Внеаудиторная самостоятельная работа обучающихся | 11 | |||||||||||||||
| Производные и дифференциалы высших порядков. Исследование функций и построение графиков. | 11 | |||||||||||||||
|
Тема 1.3 Изучение элементов интегрального исчисления | Содержание учебного материала | Уровень освоения | 14 | |||||||||||||
| Первообразная и неопределенный интеграл. Основные свойства неопределенного интеграла. Таблица неопределенных интегралов. Основные методы интегрирования. Определенный интеграл. Свойства определенного интеграла. | 1 | |||||||||||||||
|
Тематика учебных занятий | 3 | |||||||||||||||
|
Теоретическое обучение | 1 | |||||||||||||||
| 1. Первообразная и неопределенный интеграл. Основные свойства неопределенного интеграла. Таблица неопределенных интегралов | 1 | |||||||||||||||
|
Практические занятия | 2 | |||||||||||||||
| 1.Методы интегрирования | 2 | |||||||||||||||
| Внеаудиторная самостоятельная работа обучающихся: | 11 | |||||||||||||||
| Основные методы интегрирования. Определенный интеграл. Свойства определенного интеграла. | 11 | |||||||||||||||
|
Тематика учебных занятий | 3 | |||||||||||||||
|
Теоретическое обучение | 1 | |||||||||||||||
| Определители. Вычисление определителей. | 1 | |||||||||||||||
|
Практические занятия | 2 | |||||||||||||||
| 1.Выполнение действий над матрицами, вычисление определителей. | 2 | |||||||||||||||
| Внеаудиторная самостоятельная работа обучающихся | 8 | |||||||||||||||
| Обратная матрица. Матричные уравнения. | 8 | |||||||||||||||
| Тема 3.2 Решение систем линейных уравнений | Содержание учебного материала | Уровень освоения | 3 | |||||||||||||
| Системы линейных алгебраических уравнений. Методы решения систем линейных уравнений. Однородные системы линейных уравнений. | 1 | |||||||||||||||
|
Тематика учебных занятий | 3 | |||||||||||||||
|
Теоретическое обучение | 1 | |||||||||||||||
| Способы решения системы m линейных уравнений с n неизвестными. | 1 | |||||||||||||||
|
Практические занятия | 2 | |||||||||||||||
| Решение систем линейных алгебраических уравнений | 2 | |||||||||||||||
|
Требования к материально-техническому обеспечению Реализация программы дисциплины осуществляется при наличии учебного кабинета математики. Оборудование учебного кабинета: - посадочные места по количеству обучающихся; - рабочее место преподавателя; - стенды. Наглядные пособия: - таблицы производных, - таблицы интегралов, - опорный материал «Кривые второго порядка». Технические средства обучения: - переносное мультимедийное оборудование (ноутбук с лицензионным программным обеспечением, мультимедиапроектор, экран). Примерный перечень вопросов к дифференцированному зачету
1) Определение матрицы. Действия над матрицами. 2) Определитель матрицы 2 и 3 порядка. Свойства определителей. 3) Определение СЛАУ. Формулы Крамера, метод Гаусса и матричный способ решения СЛАУ. 4) Предел функции. Свойства пределов. 5) Методы раскрытия неопределенностей типа 6) Первый и второй замечательные пределы. 7) Производная функции. Правила дифференцирования. Производные основных элементарных функций. 8) Сложная функция. Правило дифференцирования сложной функции. 9) Производные высших порядков. 10) Определение точки максимума и минимума, экстремумов функции. Необходимое и достаточное условие точки экстремума. 11) Определение возрастания и убывания функции. Достаточное условие возрастания и убывания функции. 12) Определение выпуклости, вогнутости функции, точки перегиба. Условие выпуклости, вогнутости функции. Достаточное условие точки перегиба. 13) Определение асимптоты графика функции. Виды асимптот и их условия. 14) План полного исследования функции. 15) Определение дифференциала функции. Свойства дифференциала. 16) Первообразная функции. Неопределенный интеграл. Свойства неопределенного интеграла. 17) Таблица неопределенных интегралов. Методы вычисления интегралов. 18) Определенный интеграл. Формула Ньютона-Лейбница. 19) Виды событий. Вероятность события. Классическая формула вероятности. 20) Выборочный метод. Числовые характеристики выборки.
Приложение 2
Лист изменений, вносимых в рабочую программу дисциплины на 20__/ 20__ учебный год
Все изменения рабочей программы рассмотрены и одобрены на заседании ПЦК информационных и естественнонаучных дисциплин
Протокол от «___»________20__г. № _____
Председатель ПЦК М.Е. Куликова
РАБОЧАЯ ПРОГРАММА Наименование дисциплины Математика
Специальность 38.02.06 Финансы По программе базовой подготовки
Уровень образования основное общее образование Квалификация выпускника финансист
Форма обучения очная, заочная курс 2
2018 Рабочая программа дисциплины разработана на основе Федерального государственного образовательного стандарта (далее ФГОС) по специальности среднего профессионального образования (далее СПО) 38.02.06 Финансы.
Разработчик: Алешкова Т.Н., преподаватель Рабочая программа рассмотрена и одобрена на заседании предметно-цикловой комиссии (далее ПЦК) информационных и естественнонаучных дисциплин Протокол от «______» ___________ 201___ г. № _____ Председатель ПЦК ________________ М.Е. Куликова подпись
СОДЕРЖАНИЕ
ПАСПОРТ рабочей ПРОГРАММЫ ДИСЦИПЛИНЫ Математика Область применения программы Рабочая программа дисциплины является частью программы подготовки специалистов среднего звена в соответствии с ФГОС по специальности СПО 38.02.06 Финансы базового уровня. Дата: 2018-12-28, просмотров: 355. | ||||||||||||||||
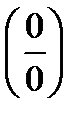 и
и 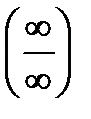 .
.