Прямая в пространстве может быть задана как линия пересечения двух плоскостей; либо точкой и направляющим вектором прямой.
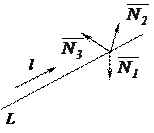 |
Прямая в пространстве не определяется через нормальный вектор, т.к. любая прямая имеет в каждой своей точке бесконечное множество нормальных векторов.
Виды уравнений прямой в пространстве
1) Каноническое уравнение прямой:
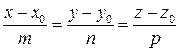 ,
,
где 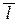 (m ; n ; p) – направляющий вектор прямой;
(m ; n ; p) – направляющий вектор прямой; 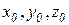 - координаты заданной точки прямой.
- координаты заданной точки прямой.
2) Уравнение прямой, проходящей через две точки М1(х1;у1; z 1) и М2(х2;у2; z 2):
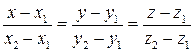 .
.
3) Общее уравнение прямой в пространстве:
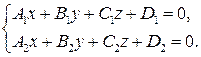
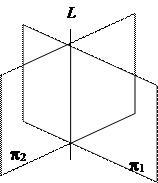
Каждое из уравнений системы является уравнением плоскости, прямая – линия пересечения двух плоскостей.
 |
4) Параметрическое уравнение прямой:
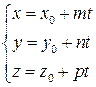 ,
,
где m , n , p – координаты направляющего вектора 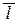 прямой;
прямой; 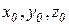 - координаты заданной точки прямой, t – параметр, -¥<t<+¥.
- координаты заданной точки прямой, t – параметр, -¥<t<+¥.
Угол между прямыми в пространстве. Условия параллельности и перпендикулярности прямых
Пусть две прямые в пространстве заданы своими каноническими уравнениями:
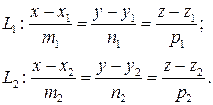
Задача определения угла между этими прямыми сводится к определению угла j между их направляющими векторами 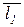 (m 1 ; n 1 ; p 1) и
(m 1 ; n 1 ; p 1) и  (m 2 ; n 2 ; p 2). По определению скалярного произведения:
(m 2 ; n 2 ; p 2). По определению скалярного произведения:
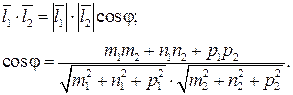
Условие параллельности прямых L 1 и L 2, эквивалентное условию коллинарности векторов 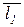 (m 1 ; n 1 ; p 1) и
(m 1 ; n 1 ; p 1) и  (m 2 ; n 2 ; p 2), заключается в пропорциональности координат их направляющих векторов:
(m 2 ; n 2 ; p 2), заключается в пропорциональности координат их направляющих векторов:
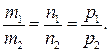
Условие перпендикулярности прямых L 1 и L 2 выражается равенством нулю скалярного произведения векторов 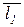 и
и 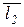 :
:
m 1 m 2 + n 1 n 2 + p 1 p 2 =0.
Условие принадлежности прямых одной плоскости
Две прямые L 1 и L 2 в пространстве могут: пересекаться, быть параллельными, скрещиваться. В первых двух случаях прямые лежат в одной плоскости.
Для принадлежности одной плоскости прямых L 1 и L 2, заданных каноническими уравнениями:
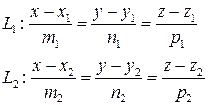 ,
,
необходимо и достаточно, чтобы три вектора 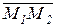 (x 2 - x 1 , y 2 - y 1 , z 2 - z 1),
(x 2 - x 1 , y 2 - y 1 , z 2 - z 1), 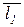 (m 1 ; n 1 ; p 1) и
(m 1 ; n 1 ; p 1) и 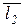 (m 2 ; n 2 ; p 2) были компланарны. Тогда необходимым и достаточным условием принадлежности двух прямых L 1 и L 2 одной плоскости является равенство нулю их смешанного произведения:
(m 2 ; n 2 ; p 2) были компланарны. Тогда необходимым и достаточным условием принадлежности двух прямых L 1 и L 2 одной плоскости является равенство нулю их смешанного произведения:
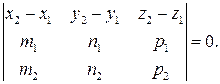
Если прямые удовлетворяют этому условию, то они либо пересекаются, либо параллельны. Определить, как эти прямые располагаются в плоскости, позволяет условие параллельности прямых.
Прямая 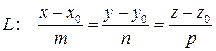 принадлежит плоскости p: Ах+ By + Cz + D =0, если выполнены два условия:
принадлежит плоскости p: Ах+ By + Cz + D =0, если выполнены два условия:
Ax0+By0+Cz0+D=0;
Am+Bn+Cp=0.
Первое из них означает, что точка М0(x 0 , y 0 , z 0), через которую проходит прямая, принадлежит плоскости, а второе есть условие параллельности прямой и плоскости.
Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости
Дата: 2018-12-28, просмотров: 317.