Линейная алгебра.
Аналитическая геометрия
Учебное пособие
Северодвинск
2005
УДК 512
Лобанова И.С., Савченко Е.В., Шерягин И.В. Линейная алгебра. Аналитическая геометрия. Учебное пособие. – Северодвинск: РИО Севмашвтуза, 2005. – 88 с.
Ответственный редактор к.т.н., доцент И.С. Лобанова.
Рецензенты: зав. кафедрой алгебры и геометрии ПГУ им. М.В.Ломоносова
к.ф.-м. н., доцент П.Д. Андреев;
к.т. н., доцент Севмашвтуза Л.В.Кремлева.
Учебное пособие предназначено для студентов, обучающихся по заочной форме обучения, которые изучают курс высшей математики. Пособие рассчитано на первый семестр обучения, включает в себя теоретический и практический материал по двум разделам: линейная алгебра и аналитическая геометрия. В учебное пособие входит расчетно-графическая работа за I семестр обучения, задачи с решениями, необходимыми для выполнения работы. Учебное пособие ставит своей целью обеспечение усвоения студентами данного курса.
| ISBN 5-7723-0578-6 | © Севмашвтуз, 2005 г. |
| Оглавление | |
| Введение | 4 |
| 1. Матрицы и определители | 5 |
| 1.1. Понятие матрицы | 5 |
| 1.2. Алгебраические операции над матрицами | 6 |
| 1.3. Определители и их свойства | 8 |
| 1.4. Обратная матрица | 11 |
| 1.5. Ранг матрицы | 12 |
| 1.6.Системы линейных уравнений | 14 |
| 2. Векторная алгебра | 21 |
| 2.1. Понятие вектора | 21 |
| 2.2. Линейные операции над векторами | 22 |
| 2. 3. Проекция вектора на ось | 23 |
| 2.4. Линейная зависимость векторов | 24 |
| 2.5. Базис. Координаты вектора | 24 |
| 2.6. Прямоугольная (декартова) система координат | 25 |
| 2.7. Скалярное произведение векторов | 26 |
| 2.8. Векторное произведение векторов | 27 |
| 2.9. Смешанное произведение векторов | 28 |
| 3. Прямые и плоскости | 30 |
| 3.1. Определение прямой на плоскости | 30 |
| 3.2. Виды уравнений прямой на плоскости | 30 |
| 3.3. Угол между двумя прямыми. Условие параллельности и перпендикулярности двух прямых | 31 |
| 3.4. Определение плоскости в пространстве | 31 |
| 3.5. Виды уравнений плоскости | 32 |
| 3.6. Угол между двумя плоскостями. Условия параллельности и перпендикулярности плоскостей | 33 |
| 3.7. Определение прямой в пространстве | 33 |
| 3.8. Виды уравнений прямой в пространстве | 34 |
| 3.9. Угол между прямыми в пространстве. Условия параллельности и перпендикулярности прямых | 34 |
| 3.10. Условие принадлежности прямых одной плоскости | 35 |
| 3.11. Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости | 37 |
| 4. Кривые второго порядка | 37 |
| 4.1. Эллипс | 37 |
| 4.2. Гипербола | 38 |
| 4.3. Парабола | 39 |
| Пример расчетно-графической работы и образец ее решения | 40 |
| Варианты заданий | 58 |
| Рекомендуемая литература | 88 |
ВВЕДЕНИЕ
Учебное пособие курса «Линейная алгебра. Аналитическая геометрия» предназначено для студентов, обучающихся по заочной форме обучения по специальности 06.08.00 «Экономика», изучающих курс высшей математики.
Настоящее пособие разработано в соответствии с требованиями Государственного стандарта Министерства образования РФ 2000 года по подготовке специалистов по специальности экономист-менеджер.
Особенность учебного пособия состоит в том, что в нем в аккумулятивной форме отражены все основные положения курса. Каждый раздел пособия содержит все наиболее существенные определения и теоремы и снабжен большим количеством примеров.
Необходимость в таком пособии обусловлена тем, что в настоящее время имеющиеся учебники, во-первых, объемны, во вторых, большинство из них содержат либо только теоретические положения, либо задания и не содержат примеров решения. Кроме того, студентам, особенно заочного отделения, бывает крайне затруднительно извлекать из множества источников необходимую информацию для усвоения вопросов курса высшей математики.
Матрицы и определители
Понятие матрицы
Матрицей называется всякая таблица элементов, состоящая из m строк и n столбцов.
Говорят, что число m ´ n называется размерностью матрицы.
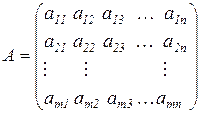 |
Обозначение:
Размерность: dimA=m ´ n. 
аij-элемент матрицы, стоящий в i-той строке и j-том столбце.
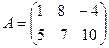 |
Пример.
размерность матрицы: dimA=2 ´ 3, элементы матрицы: a23=10, a12=8.
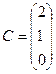 |
В =(1 4 5 -6)
- матрица-строка , dimB=1´4.
- матрица-столбец, dimC=3´1
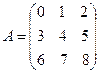
При m=n матрица называется квадратной, число n называется порядком матрицы.
Пример.
- квадратная матрица третьего порядка, n=3
Элементы квадратной матрицы аij при i=j образуют главную диагональ матрицы.
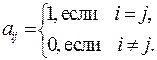 |
Квадратная матрица, образованная элементами
называется единичной матрицей.
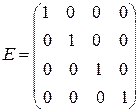 |
Пример. Единичная матрица 4-го порядка.
Нулевая матрица - матрица, у которой все элементы равны нулю.
Нулевая матрица может быть любой размерности.
Матрица, все элементы которой выше либо ниже главной диагонали равны нулю, называется треугольной матрицей.
Пример. А- треугольная матрица.
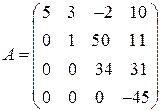 |
Дата: 2018-12-28, просмотров: 370.