Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

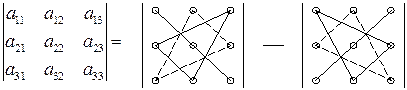
Правило треугольников:

=а₁₁а₂₂а₃₃ +а₁₂а₂₃а₃₁+ а₁₃а₂₁а₃₂-(а₁₂а₂₁а₃₃+а₁₁а₂₃а₃₂+а₁₃а₂₂а₃₁).

Пример.

 

 

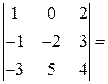
=1×(-2)×4+2×(-1)×5+0×3×(-3)-[2×(-2)×(-3)+1×3×5+0×(-1)×4] = -27-18= -45

 

1.3.3. Вычисление определителей разложением по строке (столбцу) 

Пусть А- квадратная матрица порядка n.

Алгебраическим дополнением A_ij элемента матрицы a_ij называется определитель (n-1)-го порядка, полученный из исходного вычеркиванием i-той строки и j-того столбца, взятый со знаком «+», если сумма i + j четная, и со знаком «-», если нечетная.

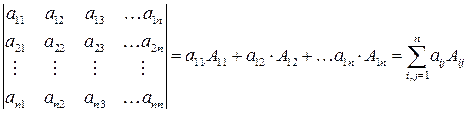Определитель порядка n>1 равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения.

 

Пример. Вычислить определитель разложением по строке либо столбцу.

  

 

 

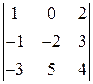
Разложим определитель по первой строке.

 

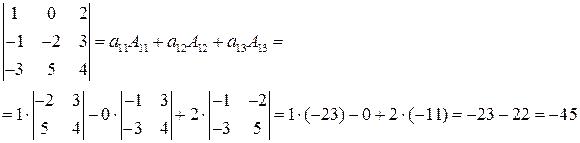 Ответ: -45.

 

1.3.4. Вычисление определителей путем приведения матрицы к треугольному виду.

Этот метод называют также методом элементарных преобразований.

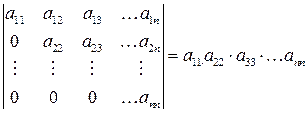Определитель треугольной матрицы равен произведению элементов главной диагонали.

 

Произвольная матрица приводится к треугольному виду методом элементарных преобразований.

Под элементарными преобразованиями понимают умножение какой-либо строки (столбца) на число l¹0 и добавление к другой строке (столбцу).

Замечание. Элементарные преобразования обратимы, т.е. если матрица А может быть получена из матрицы В элементарными преобразованиями, то матрица В также может быть получена из А обратными им элементарными преобразованиями.

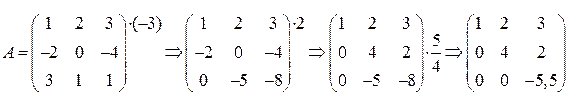Пример.

 

1. Умножим первую строку матрицы на (-3) и прибавим ее ко второй строке. Результат запишем во второй строке новой матрицы.

2. Умножим первую строку матрицы на 2 и прибавим ее к третьей строке. Результат запишем в третьей строке новой матрицы.

3. Умножим вторую строку матрицы на 5/4 и прибавим ее к третьей строке. Результат запишем в третьей строке новой матрицы.

Получим треугольную матрицу, определитель которой равен произведению элементов главной диагонали.

 detA=1×4×(-5,5)= -22

Ответ:  -22.

 

Свойства определителей

1) При транспонировании матрицы определитель не изменяется, т.е. detA=det(A^T)

2) При перестановке двух строк (столбцов) определитель меняет знак на обратный.

3) При круговой перестановке строк (столбцов) определитель не изменяется.

4) Если в определителе есть две одинаковые строки (столбца), то определитель равен 0; если одна из строк (столбцов) матрицы получается из другой строки (столбца) умножением на некоторый множитель, то определитель равен 0.

5) При умножении матрицы порядка n на число l определитель умножается на lⁿ.

6) При умножении одной строки (столбца) на число l определитель умножается на это число.

 

Обратная матрица