Цель: формирование навыков решения тригонометрических неравенств.

Вид работы: индивидуальный.

Время выполнения: 2 часа.

Теоретические сведения

Пример 1. Решить неравенство: .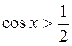

Решение. По определению 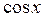– это абсцисса точки единичной ок-

ружности. Чтобы решить неравенство 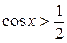, нужно выяснить, какие

точки единичной окружности имеют абсциссу, большую .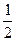

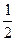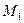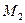Абсциссу, равную , имеют  две точки единичной окружности  и   (рис. 35.1) . Точка  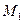получается поворотом точки 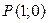на угол 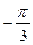, а также на углы 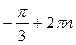, где 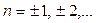. Точка  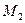получается поворотом точки 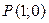на угол 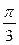, а также на углы 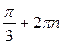, где .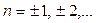

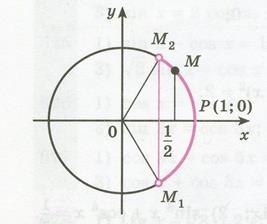
Рисунок 35.1 - Решение неравенства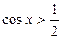

Абсциссу, большую 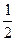, имеют  все точки 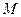дуги единичной окружности, лежащие правее прямой 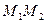. Таким образом, решениями неравенства  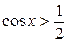являются все числа  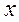из промежутка 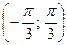. Все решения данного неравенства – множество интервалов: , .

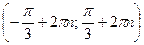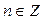Пример 2. Решить неравенство: .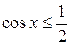

Решение. Абсциссу, не большую 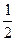, имеют  все точки дуги  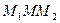единичной окружности (рис. 35.2). Поэтому решениями неравенства  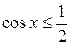являются числа 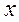, которые принадлежат отрезку 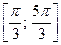. Все решения данного неравенства – множество отрезков: , .

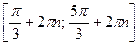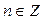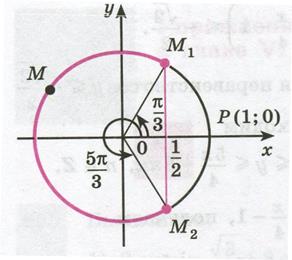
Рисунок 35.2 - Решение неравенства

Пример 3. Решить неравенство: .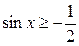

Решение. Ординату, не меньшую 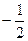, имеют все точки дуги  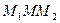единичной окружности (рис. 35.3).

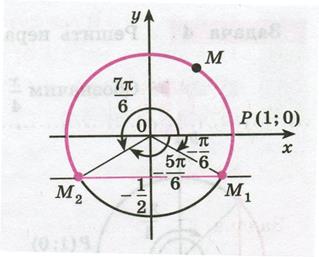
Рисунок 35.3 - Решение неравенства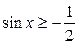

Поэтому решениями неравенства 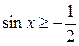 являются числа 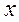, которые принадлежат отрезку 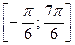. Все решения данного неравенства – множество отрезков: , .

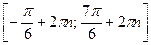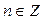Отметим, что все точки окружности, лежащие ниже прямой 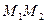, имеют ординату, меньшую 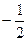(рис. 35.3). Поэтому все числа  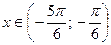являются решениями неравенства .

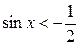Все решения этого неравенства – интервалы: , .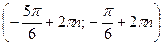

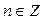Задания к практической работе

Задание 1. Решить неравенство:

1. 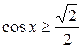;	2. 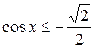;	3. ;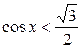
4. 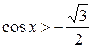;	5. 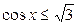;	6. ;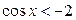
7. 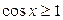;	8. 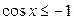;	9. ;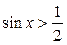
10. 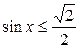;	11.	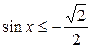12.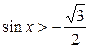
13. 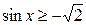;	14. 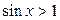;	15. ;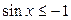
16. 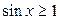;	17. 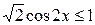;	18. ;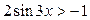
19. 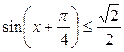;	20. 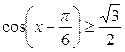;	21. .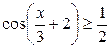

Контрольные вопросы

1. Какие неравенства называются тригонометрическими?

2. Какими способами можно решить простейшее тригонометрическое неравенство?

Рекомендуемая литература: 1.1, 1.3, 1.4.

Практическая работа № 36

Тема: Использование свойств и графиков функций

Для решения уравнений и неравенств

Цель: формирование навыков решения уравнений и неравенств с

помощью графиков функций.

Вид работы: индивидуальный.

Время выполнения: 2 часа.

Теоретические сведения

Пример 1. Выяснить с помощью графиков, сколько корней имеет уравнение 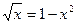. Найти приближенные значения этих корней.

Решение: Построим на одном рисунке графики функци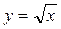й  и 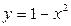 (рис. 36.1). Графики пересекаются в одной точке при .

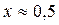Ответ: .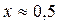

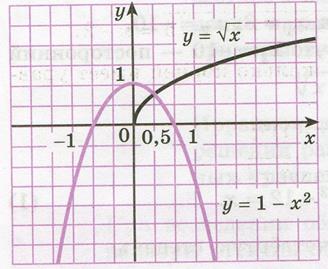
Рисунок 36.1 - графики функци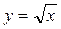й  и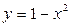

Пример 2. С помощью графиков решить неравенство: .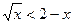

Решение: Построим на одном рисунке графики функци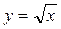й  и  (рис. 36.2) и выясним, при каких значениях 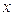 точки графика функции 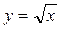лежат ниже точек графика функции .

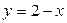Из рисунка видно, что эти графики пересекаются в одной точке, абсцисса которой является корнем уравнения 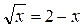. Этот корень 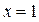. График функции 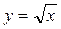лежит ниже графика функци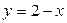и  при .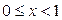

Ответ: .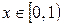

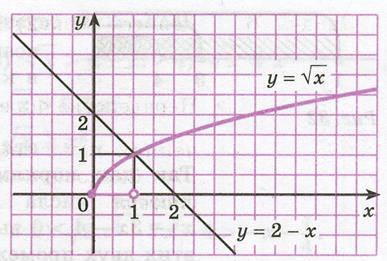
Рисунок 36.2 - Графики функци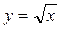й  и

Задания к практической работе

Задание 1. Выяснить с помощью графиков, сколько корней имеет уравнение:

1. 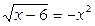;	2. ;
3. 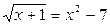;	4. .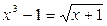

Задание 2. Решить графически неравенство:

1. 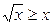;	2. ;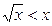
3. ;	4. ;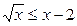
5. 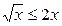;	6. ;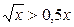
7. 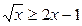;	8. .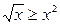

Контрольные вопросы

1. Как с помощью графиков решить уравнение?

2. Как с помощью графиков решить неравенство?

Рекомендуемая литература: 1.1, 1.3, 1.4.

Практическая работа № 37