Многие тригонометрические уравнения, правая часть которых равна нулю, решаются разложением их левой части на множители.
Пример 8. Решить уравнение 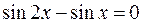 .
.
Решение: для решения данного уравнения используем формулу:
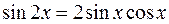 ; получаем:
; получаем:
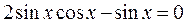 , выносим
, выносим 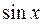 за скобки
за скобки
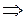
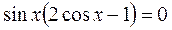
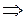
1) 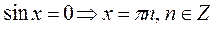 ;
;
2)  .
.
Ответ: 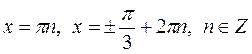 .
.
Пример 9. Решить уравнение 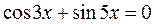 .
.
Решение: используем формулу приведения 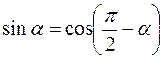 и запишем исходное уравнение в виде:
и запишем исходное уравнение в виде:
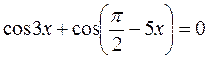 .
.
Используем формулу суммы косинусов 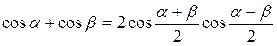 , получаем:
, получаем: 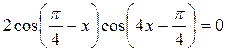 или
или 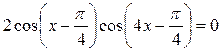 .
.
1) 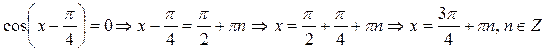
2) 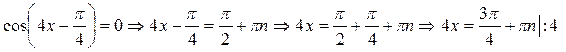
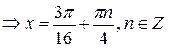
Ответ: 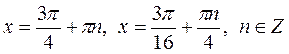 .
.
Пример 10. Решить уравнение 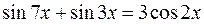 .
.
Решение: применим формулу для суммы синусов: 
Получаем:
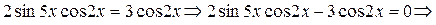
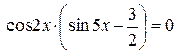
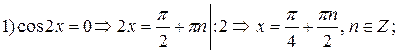
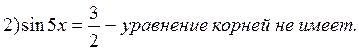
Ответ: 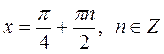 .
.
Пример 11. Решить уравнение 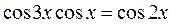 .
.
Решение: 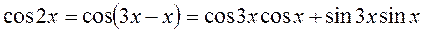
Поэтому, исходное уравнение примет вид:
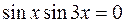
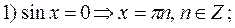
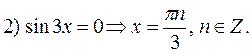
Заметим, что числа 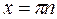 содержатся среди чисел вида
содержатся среди чисел вида 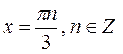 , так как если
, так как если 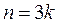 , то
, то 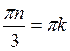 . Следовательно, первая серия корней содержится во второй.
. Следовательно, первая серия корней содержится во второй.
Ответ: 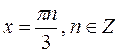
Задания к практической работе
Задание 1. Решить уравнение:
1. 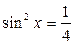 ; ;
| 2. 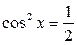 ; ;
|
3. 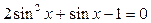 ; ;
| 4. 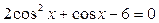 ; ;
|
5. 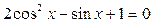 ; ;
| 6. 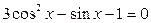 ; ;
|
7. 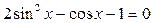 ; ;
| 8. 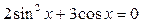 ; ;
|
9. 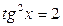 ; ;
| 10. 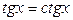 ; ;
|
11. 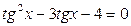 ; ;
| 12. 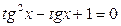 ; ;
|
13. 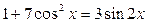 ; ;
| 14. 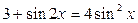 ; ;
|
15. 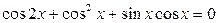 ; ;
| 16. 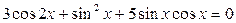 ; ;
|
17. 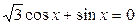 ; ;
| 18. 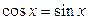 ; ;
|
19. 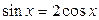 ; ;
| 20. 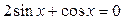 ; ;
|
21. 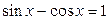 ; ;
| 22. 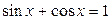 ; ;
|
23. 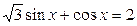 ; ;
| 24. 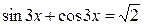 ; ;
|
25. 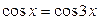 ; ;
| 26. 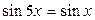 ; ;
|
27. 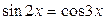 ; ;
| 28. 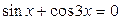 ; ;
|
29. 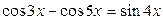 ; ;
| 30. 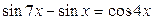 ; ;
|
31. 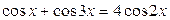 ; ;
| 32. 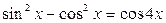 ; ;
|
33. 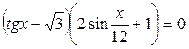 ; ;
| 34. 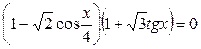 ; ;
|
35. 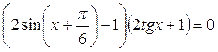 ; ;
| 36. 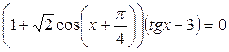 ; ;
|
Задание 2. Найти все значения a, при которых уравнение
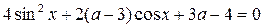 имеет корни, и решить это уравнение.
имеет корни, и решить это уравнение.
Контрольные вопросы
1. Какие уравнения называются тригонометрическими?
2. Что называется корнем тригонометрического уравнения?
3. По каким формулам находят решения простейших тригонометрических уравнений?
Рекомендуемая литература: 1.1, 1.3, 1.4.
Практическая работа № 34
Тема: Показательные, логарифмические неравенства
Цель: формирование навыков решения показательных и логарифмических неравенств.
Вид работы: индивидуальный.
Время выполнения: 2 часа.
Теоретические сведения
Решение показательных неравенств часто сводится к решению нера- венств 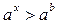 или
или 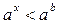 .
.
Эти неравенства решаются с помощью свойства возрастания или убывания показательной функции: для возрастающей функции большему значению функции соответствует большее значение аргумента, а для убывающей функции большему значению функции соответствует меньшее значение аргумента.
Пример 1. Решить неравенство: 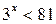 .
.
Решение. Запишем неравенство в виде 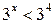 . Так как
. Так как 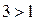 , то функция
, то функция 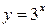 является возрастающей. Поэтому решениями неравенства
является возрастающей. Поэтому решениями неравенства 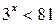 являются числа
являются числа 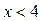 .
.
Ответ: 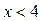
Пример 2. Решить неравенство: 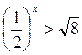 .
.
Решение. Запишем неравенство в виде 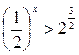 , или
, или 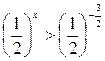 .
.
Так как функция 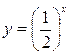 - убывающая функция, то
- убывающая функция, то 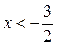 .
.
Ответ: 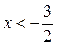 .
.
Пример 3. Решить неравенство: 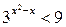 .
.
Решение. Запишем неравенство в виде 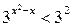 . Так как
. Так как 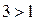 , то
, то 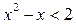 , откуда
, откуда 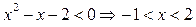 .
.
Ответ: 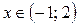 .
.
Пример 4. Решить неравенство: 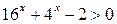 .
.
Решение. Пусть 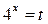 , тогда получим квадратное неравенство
, тогда получим квадратное неравенство 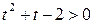 . Решаем его и получаем:
. Решаем его и получаем:  и
и 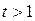 . Вернемся к замене:
. Вернемся к замене:
1) 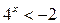 - не имеет решений, так как
- не имеет решений, так как 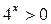 при всех
при всех 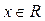 .
.
2) 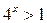
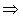
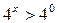
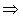
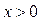 .
.
Ответ: 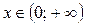 .
.
Пример 5. Решить графически уравнение: 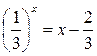 .
.
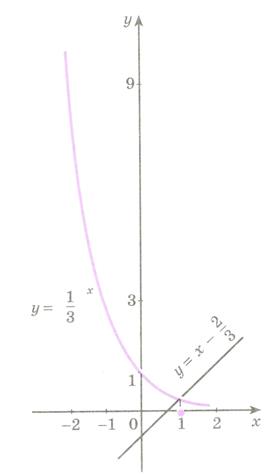
Рисунок 34.1 – графики функций 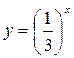 и
и 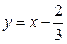
Решение. В одной системе координат построим графики функций
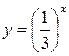 и
и 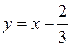 (рис. 34.1). Из рисунка видно, что графики этих функций пересекаются в точке с абсциссой
(рис. 34.1). Из рисунка видно, что графики этих функций пересекаются в точке с абсциссой 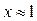 .
.
Проверка показывает, что 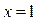 - корень данного уравнения:
- корень данного уравнения:
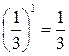 и
и 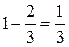 .
.
Ответ: 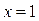 .
.
При изучении логарифмической функции рассматривались неравенства вида: 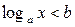 и
и 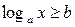 . Приведем примеры решения более сложных логарифмических неравенств. Обычный способ решения таких неравенств заключается в переходе от них к более простому неравенству или системе неравенств, имеющей то же самое множество решений, т.е. к равносильному неравенству или к равносильной системе неравенств.
. Приведем примеры решения более сложных логарифмических неравенств. Обычный способ решения таких неравенств заключается в переходе от них к более простому неравенству или системе неравенств, имеющей то же самое множество решений, т.е. к равносильному неравенству или к равносильной системе неравенств.
Пример 6. Решить неравенство: 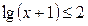 .
.
Решение. ОДЗ: 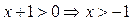 .
.
Исходное неравенство запишем так: 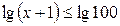 . Так как
. Так как 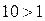 , то
, то 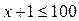 , откуда
, откуда 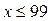 . Учитывая ОДЗ, получаем
. Учитывая ОДЗ, получаем 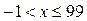 .
.
Ответ: 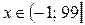
Пример 7. Решить неравенство: 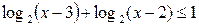 .
.
Решение. ОДЗ: 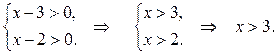 .
.
По свойствам логарифма исходное неравенство при 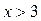 равносильно неравенству:
равносильно неравенству: 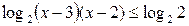 . Так как
. Так как 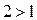 , то
, то 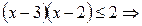
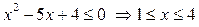 . Учитывая ОДЗ, получаем
. Учитывая ОДЗ, получаем 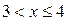 .
.
Ответ: 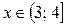
Задания к практической работе
Задание 1. Решить неравенство:
1. 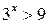 ; ;
| 2. 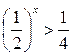 ; ;
| 3. 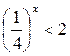 ; ;
|
4. 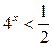 ; ;
| 5. 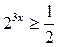 ; ;
| 6. 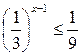 ; ;
|
7. 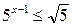 ; ;
| 8.  ; ;
| 9. 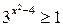 ; ;
|
10. 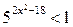 ; ;
| 11. 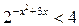 ; ;
| 12. 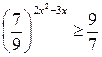 ; ;
|
13. 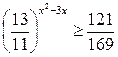 ; ;
| 14. 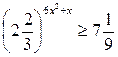 ; ;
| 15. 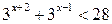 ; ;
|
16. 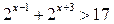 ; ;
| 17. 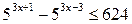 ; ;
| 18. 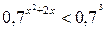 . .
|
Задание 2. Решить графически уравнение:
1. 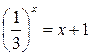 ; ;
| 2. 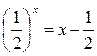 ; ;
|
3. 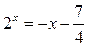 ; ;
| 4. 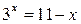 . .
|
Задание 3. Найти целые решения неравенства на отрезке 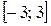 :
:
1. 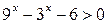 ; ;
| 2. 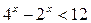 ; ;
|
3. 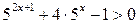 ; ;
| 4. 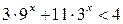 . .
|
Задание 4. Найти область определения функции:
1. 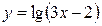 ; ;
| 2. 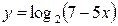 ; ;
|
3. 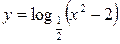 ; ;
| 4. 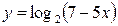 . .
|
Задание 5. Решить неравенство:
1. 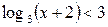 ; ;
| 2. 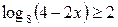 ; ;
|
3. 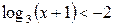 ; ;
| 4. 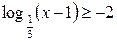 ; ;
|
5. 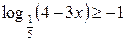
| 6. 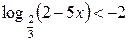 ; ;
|
7. 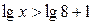 ; ;
| 8. 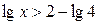 ; ;
|
9. 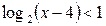 ; ;
| 10. 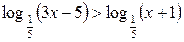 ; ;
|
11. 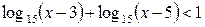 ; ;
| 12. 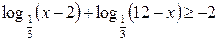 ; ;
|
13. 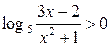 ; ;
| 14. 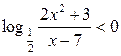 ; ;
|
15. 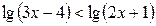 ; ;
| 16. 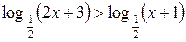 ; ;
|
17. 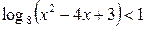 ; ;
| 18. 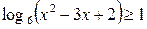 ; ;
|
19. 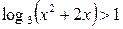 ; ;
| 20. 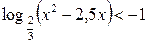 . .
|
Контрольные вопросы
1. Какие неравенства называются показательными?
2. Какие неравенства называются логарифмическими?
Рекомендуемая литература: 1.1, 1.3, 1.4.
Практическая работа № 35
Дата: 2018-12-28, просмотров: 453.