ОУДп.01 МАТЕМАТИКА: АЛГЕБРА, НАЧАЛА

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

ОУДп.01 МАТЕМАТИКА: АЛГЕБРА, НАЧАЛА

МАТЕМАТИЧЕСКОГО АНАЛИЗА, ГЕОМЕТРИЯ

Методические указания по выполнению практических работ

по дисциплине ОУДп.01 Математика: алгебра и начала

математического анализа, геометрия

для обучающихся по всем специальностям

очной формы обучения

(часть 5)

Составитель С.И. Москалевская,

Преподаватель высшей квалификационной категории

Тюмень

ТИУ

2018

ОУДп.01 Математика: алгебра, начала математического анализа, геометрия методические указания по выполнению практических работ по дисциплине ОУДп.01 Математика: алгебра, начала математического анализа, геометрия для обучающихся по всем специальностям очной формы обучения (часть 5) / сост. Москалевская С. И.; Тюменский индустриальный университет. – Тюмень: Издательский центр БИК, ТИУ, 2018. –28 с.

Ответственный редактор: Т.М. Белкина, председатель цикловой комиссии общеобразовательных дисциплин.

Методические указания рассмотрены и рекомендованы к изданию на заседании цикловой комиссии общеобразовательных дисциплин

«18» января 2018 года, протокол №1

Аннотация

Методические указания по дисциплине ОУДп.01 Математика: алгебра, начала математического анализа, геометрия предназначены для обучающихся по всем специальностям очной формы обучения.

Методические указания по дисциплине ОУДп.01 Математика: алгебра, начала математического анализа, геометрия составлены в соответствии с рабочей программой и состоят из содержания практических работ, пояснительной записки, общих требований по выполнению практических работ, критериев оценки выполнения и контрольных вопросов.

Методические указания могут оказать помощь преподавателям в организации самостоятельных работ, а также могут использоваться обучающимися при подготовке к занятиям и экзамену.

Содержание

Пояснительная записка	4
Общие требования к выполнению и оформлению практических работ	4
Критерии оценки практических работ	5
Практическая работа № 33 Тригонометрические уравнения	5
Практическая работа № 34 Показательные и логарифмические неравенства	11
Практическая работа № 35 Тригонометрические неравенства	15
Практическая работа № 36 Использование свойств и графиков функций для решения уравнений и неравенств	18
Практическая работа № 37 История развития комбинаторики, её роль в различных сферах человеческой деятельности. Правила комбинаторики. Решение комбинаторных задач. Размещения, сочетания и перестановки	20
Список литературы	26

Пояснительная записка

Методические указания по выполнению практических работ составлены в соответствии с рабочей программой по дисциплине ОУДп.01 Математика: алгебра, начала математического анализа, геометрия на базе основного общего образования.

Практические работы занимают важное место при изучении дисциплины ОУДп.01 Математика: алгебра и начала математического анализа, геометрия. Цель изучения дисциплины состоит в формировании знаний, практических умений и навыков решения элементарных математических задач.

В результате выполнения практических работ обучающийся должен:

иметь представление:

- о месте и роли математики в современном мире, общности ее понятий и представлений;

- о логическом строении дисциплины;

- о междисциплинарной связи математики со специальными дисциплинами;

знать и уметь:

- теоретические разделы каждой темы;

уметь:

- решать примеры и задачи по каждой теме.

Методические указания по выполнению практических работ состоят из пояснительной записки, критериев оценки работы, общих требований к выполнению и оформлению практических занятий, содержания практических занятий, которые снабжены основными теоретическими положениями, заданиями, контрольными вопросами и списком литературы.

На выполнение каждой работы отводится определенное количество часов в соответствии с тематическим планом.

Форма отчетности указана для каждого практического занятия.

Методические указания по выполнению практических работ окажут помощь преподавателям в организации и управлении работой обучающихся в процессе занятий, а обучающиеся могут использовать их как пособие для повторения изученного материала, подготовке к экзамену.

ОБЩИЕ ТРЕБОВАНИЯ К ВЫПОЛНЕНИЮ

ПРАКТИЧЕСКИХ РАБОТ

Практические задания должны оформляться в отдельной тетради и содержать:

- тему, цель, вид работы, время выполнения практического задания;

- условия заданий;

- необходимые расчетные формулы, понятия;

- подробные решения заданий;

- для успешной защиты отчета по практическим заданиям обучающийся должен правильно ответить на рекомендуемые контрольные вопросы, проявить навыки решения задач и умение иллюстрировать теоретический материал расчетами для выполненных заданий.

- отчет должен заключаться выводом о практической работе.

Практическая работа № 33

Теоретические сведения

В практической работе № 20 были показаны формулы корней простейших тригонометрических уравнений 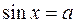, , 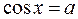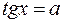. К этим уравнениям сводятся другие тригонометрические уравнения. Для решения большинства таких уравнений требуется применение различных формул и преобразований тригонометрических выражений. Рассмотрим

некоторые примеры решения тригонометрических уравнений.

Практическая работа № 34

Теоретические сведения

Решение показательных неравенств часто сводится к решению нера- венств 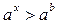или .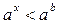

Эти неравенства решаются с помощью свойства возрастания или убывания показательной функции: для возрастающей функции большему значению функции соответствует большее значение аргумента, а для убывающей функции большему значению функции соответствует меньшее значение аргумента.

Пример 1. Решить неравенство: .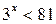

Решение. Запишем неравенство в виде 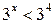. Так как 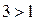, то функция 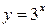является возрастающей. Поэтому решениями неравенства 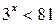являются числа .

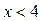Ответ: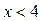

Пример 2. Решить неравенство: .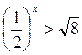

Решение. Запишем неравенство в виде 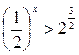, или .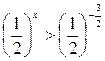

Так как функция 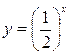- убывающая функция, то .

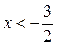Ответ: .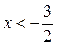

Пример 3. Решить неравенство: .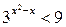

Решение. Запишем неравенство в виде 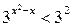. Так как 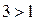, то 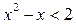, откуда .

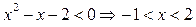Ответ: .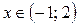

Пример 4. Решить неравенство: .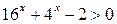

Решение. Пусть 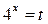, тогда получим квадратное неравенство 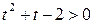. Решаем его и получаем: и 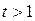. Вернемся к замене:

1) 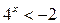- не имеет решений, так как 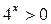при всех .

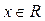2) .

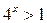
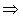
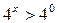
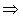
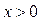Ответ: .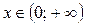

Пример 5. Решить графически уравнение: .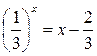

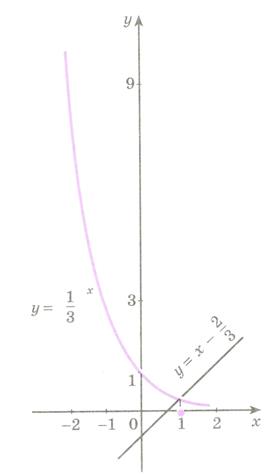
Рисунок 34.1 – графики функци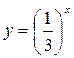й и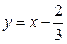

Решение. В одной системе координат построим графики функци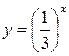й

и 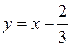(рис. 34.1). Из рисунка видно, что графики этих функций пересекаются в точке с абсциссой .

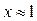Проверка показывает, что 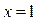- корень данного уравнения:

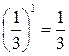и .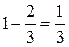

Ответ: .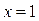

При изучении логарифмической функции рассматривались неравенства вида: 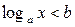и 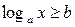. Приведем примеры решения более сложных логарифмических неравенств. Обычный способ решения таких неравенств заключается в переходе от них к более простому неравенству или системе неравенств, имеющей то же самое множество решений, т.е. к равносильному неравенству или к равносильной системе неравенств.

Пример 6. Решить неравенство: .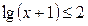

Решение. ОДЗ: .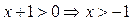

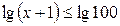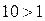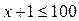Исходное неравенство запишем так: . Так как , то , откуда 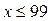. Учитывая ОДЗ, получаем .

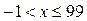Ответ: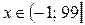

Пример 7. Решить неравенство: .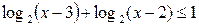

Решение. ОДЗ: .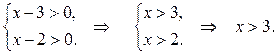

По свойствам логарифма исходное неравенство при 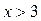равносильно неравенству: 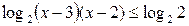. Так как 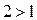, то 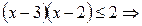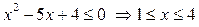. Учитывая ОДЗ, получаем .

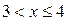Ответ: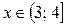

Задания к практической работе

Задание 1. Решить неравенство:

1. 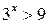;	2. 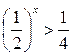;	3. ;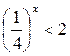
4. 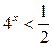;	5. 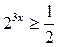;	6. ;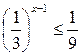
7. 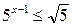;	8. ;	9. ;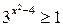
10. 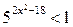;	11. 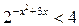;	12. ;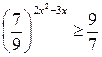
13. 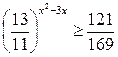;	14. 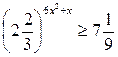;	15. ;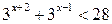
16. 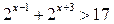;	17. 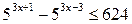;	18. .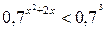

Задание 2. Решить графически уравнение:

1. 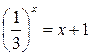;	2. ;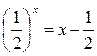
3. 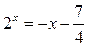;	4. .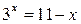

Задание 3. Найти целые решения неравенства на отрезке :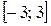

1. 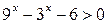;	2. ;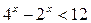
3. 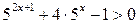;	4. .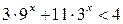

Задание 4. Найти область определения функции:

1. 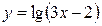;	2. ;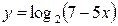
3. 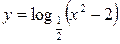;	4. .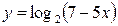

Задание 5. Решить неравенство:

1. 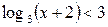;	2. ;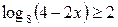
3. 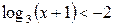;	4. ;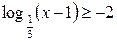
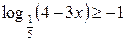
5.	6. ;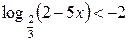
7. 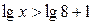;	8. ;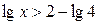
9. 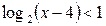;	10. ;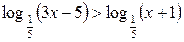
11. 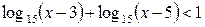;	12. ;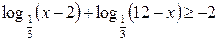
13. 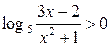;	14. ;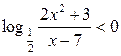
15. 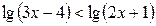;	16. ;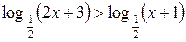
17. 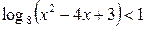;	18. ;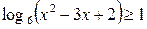
19. 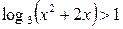;	20. .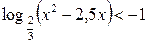

Контрольные вопросы

1. Какие неравенства называются показательными?

2. Какие неравенства называются логарифмическими?

Рекомендуемая литература: 1.1, 1.3, 1.4.

Практическая работа № 35

Теоретические сведения

Пример 1. Решить неравенство: .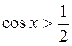

Решение. По определению 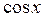– это абсцисса точки единичной ок-

ружности. Чтобы решить неравенство 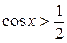, нужно выяснить, какие

точки единичной окружности имеют абсциссу, большую .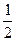

Абсциссу, равную 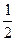, имеют две точки единичной окружност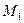и и 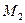(рис. 35.1) . Точка 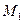получается поворотом точки 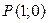на угол 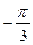, а также на углы 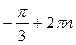, где 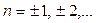. Точка 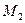получается поворотом точки 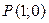на угол 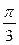, а также на углы 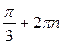, где .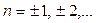

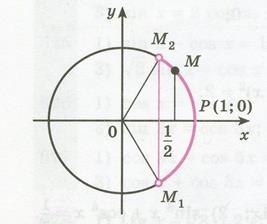
Рисунок 35.1 - Решение неравенства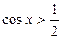

Абсциссу, большую 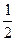, имеют все точки 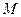дуги единичной окружности, лежащие правее прямой 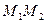. Таким образом, решениями неравенства 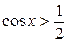являются все числа 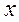из промежутка 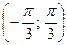. Все решения данного неравенства – множество интервалов: , .

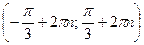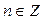Пример 2. Решить неравенство: .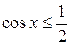

Решение. Абсциссу, не большую 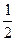, имеют все точки дуги 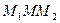единичной окружности (рис. 35.2). Поэтому решениями неравенства 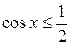являются числа 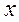, которые принадлежат отрезку 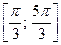. Все решения данного неравенства – множество отрезков: , .

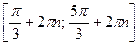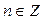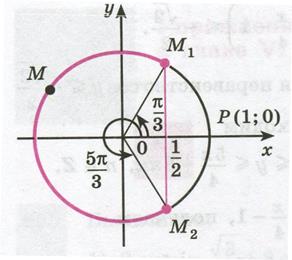
Рисунок 35.2 - Решение неравенства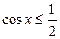

Пример 3. Решить неравенство: .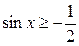

Решение. Ординату, не меньшую 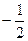, имеют все точки дуги 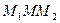единичной окружности (рис. 35.3).

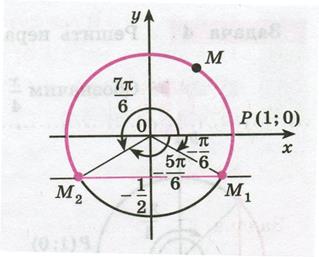
Рисунок 35.3 - Решение неравенства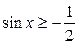

Поэтому решениями неравенства 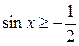являются числа 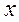, которые принадлежат отрезку 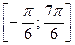. Все решения данного неравенства – множество отрезков: , .

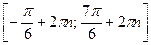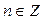Отметим, что все точки окружности, лежащие ниже прямой 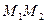, имеют ординату, меньшую 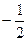(рис. 35.3). Поэтому все числа 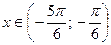являются решениями неравенства .

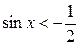Все решения этого неравенства – интервалы: , .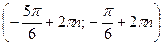

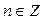Задания к практической работе

Задание 1. Решить неравенство:

1. 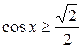;	2. 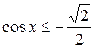;	3. ;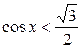
4. 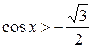;	5. 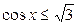;	6. ;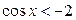
7. 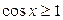;	8. 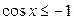;	9. ;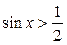
10. 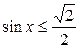;	11.	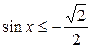12.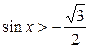
13. 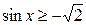;	14. 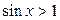;	15. ;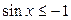
16. 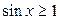;	17. 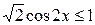;	18. ;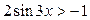
19. 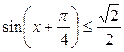;	20. 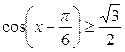;	21. .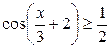

Контрольные вопросы

1. Какие неравенства называются тригонометрическими?

2. Какими способами можно решить простейшее тригонометрическое неравенство?

Рекомендуемая литература: 1.1, 1.3, 1.4.

Практическая работа № 36

Теоретические сведения

Пример 1. Выяснить с помощью графиков, сколько корней имеет уравнение 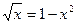. Найти приближенные значения этих корней.

Решение: Построим на одном рисунке графики функци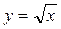й и 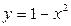(рис. 36.1). Графики пересекаются в одной точке при .

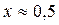Ответ: .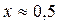

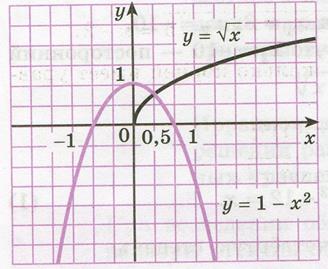
Рисунок 36.1 - графики функци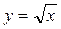й и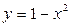

Пример 2. С помощью графиков решить неравенство: .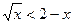

Решение: Построим на одном рисунке графики функци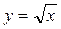й и (рис. 36.2) и выясним, при каких значениях 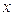точки графика функции 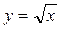лежат ниже точек графика функции .

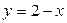Из рисунка видно, что эти графики пересекаются в одной точке, абсцисса которой является корнем уравнения 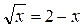. Этот корень 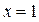. График функции 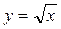лежит ниже графика функци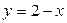и при .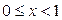

Ответ: .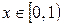

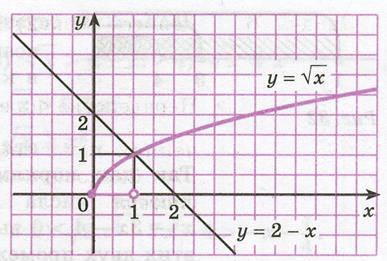
Рисунок 36.2 - Графики функци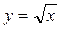й и

Задания к практической работе

Задание 1. Выяснить с помощью графиков, сколько корней имеет уравнение:

1. 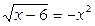;	2. ;
3. 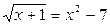;	4. .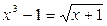

Задание 2. Решить графически неравенство:

1. 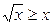;	2. ;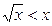
3. ;	4. ;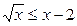
5. 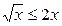;	6. ;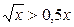
7. 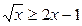;	8. .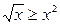

Контрольные вопросы

1. Как с помощью графиков решить уравнение?

2. Как с помощью графиков решить неравенство?

Рекомендуемая литература: 1.1, 1.3, 1.4.

Практическая работа № 37

Теоретический материал

Комбинаторика – раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. Комбинаторика связана со многими другими областями математики — алгеброй, геометрией, теорией вероятностей и имеет широкий спектр применения в различных областях знаний (например, в генетике, информатике, статистической физике).

До того, как та или иная область знания формируется в особую науку, она сначала проходит длительный период накопления эмпирического материала, потом развивается в недрах другой, более общей науки и лишь затем выделяется в самостоятельную ветвь. С задачами, в которых приходится выбирать те или иные предметы, располагать их в определенном порядке и отыскивать среди разных расположений наилучшие, люди столкнулись еще в доисторическую эпоху, выбирая наилучшие расположения охотников во время охоты, воинов во время битвы, инструментов во время работы. Определенным образом располагались украшения на одежде, узоры на керамике, перья в оперении стрелы. Ещё в древности было замечено, что имеются явления, обладающие следующей особенностью: при малом числе наблюдений над ними не замечается никакой зависимости, но по мере увеличения числа наблюдений всё яснее проявляется определенная закономерность. В рукописи ''Же Ким'' (''Книга перестановок'') показаны различные соединения этих знаков по два и по три. Восемь рисунков из трех рядов символов изображали землю, горы, воду, ветер, грозу, огонь, облака и небо (некоторые рисунки имели и иные значения). Неудивительно поэтому, что сумма первых 8 натуральных чисел (т. е. число 36) воплощала в представлениях древних китайцев весь мир. Понадобилось выразить по мере углубления знаний и другие элементы мироздания с помощью тех же знаков -- и -- --. Были составлены 64 фигуры, содержавшие уже пять рядов черточек. Надо полагать, что автор рукописи ''Же Ким'' заметил удвоенные числа рисунков при добавлении одного ряда символов. Это можно рассматривать как первый общий результат комбинаторики.

Конкретные комбинаторные задачи, касавшиеся перечисления небольших групп предметов, греки решали без ошибок. Аристотель описал без пропусков все виды правильных трехчленных силлогизмов, а его ученик Арисксен из Тарента перечислил различные комбинации длинных и коротких слогов в стихотворных размерах. Живший в IV в. н.э. математик Папп рассматривал число пар и троек, которые можно получить из трех элементов, допуская их повторения.

Области применения комбинаторики:

1. Производство (распределение нескольких видов работ между рабочими).

2. Агротехника (размещение посевов на нескольких полях).

3. Учебные заведения (составление расписаний).

4. Химия (анализ возможных связей между химическими элементами).

5. Лингвистика (рассмотрение вариантов комбинаций букв).

6. Азартные игры (подсчёт частоты выигрышей).

7. Экономика (анализ вариантов купли-продажи акций).

8. Спортивные соревнования (расчёт количества игр между участниками).

9. Военное дело (расположение подразделений).

Перестановками из 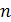элементов называются соединения, которые состоят из одних и тех же 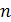элементов и отличаются одно от другого только порядком их расположения.

Число перестановок из 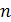элементов обозначают 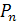и читают «пэ энное». Формула числа перестановок 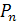из 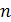различных элементов:

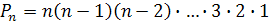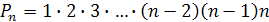Произведение первых 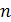натуральных чисел обозначают 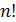(читается «эн факториал»), т. е. 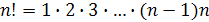, причём по определению 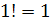. Таким образом,

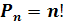(37.1)

Размещениями из 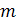элементов по 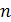элементов ( 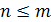) называются такие соединения, каждое из которых содержит 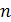элементов, взятых из данных 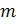разных элементов, и которые отличаются одно от другого либо самими элементами, либо порядком их расположения.

Число всевозможных размещений из 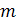элементов по 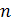элементов обозначают 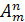и читают «А из эм по эн».

Формула для вычисления 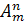- числа размещений из 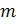элементов по 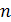элементов имеет следующий вид:

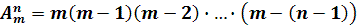(37.2)

Например, .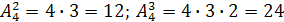

Отметим, что правая часть формулы (2) содержит произведение 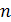последовательных натуральных чисел, наибольшее из которых равно 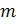. Пусть в формуле (2) 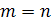. Тогда

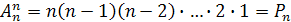
т. е. число размещений из 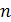элементов по 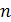равно числу перестановок из этих элементов:

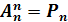(37.3)

Сочетаниями из 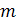элементов по 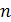в каждом ( 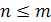) называются соединения, каждое из которых содержит 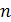элементов, взятых из данных 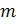разных элементов, и которые отличаются одно от другого по крайней мере одним элементом.

Число всевозможных сочетаний из 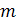различных элементов по 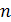элементов обозначают 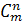и читают «це из эм по эн».

Формула для подсчёта числа сочетаний из 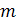различных элементов по 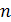элементов в каждом имеет следующий вид:

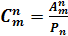(37.4)

Рассмотрим свойства сочетаний, которые в ряде случаев упрощают вычисления при решении задач.

1. .

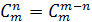2. Рекуррентное свойство

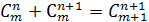
Пример 1. Сколько различных двузначных чисел можно записать с помощью цифр 0, 1, 2, 3?

Решение. В качестве первой цифры может быть выбрана любая из цифр 1, 2, 3 (т. е. 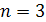). Второй цифрой может быть выбрана любая из четырёх данных цифр 0, 1, 2, 3 (т. е. 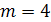). Согласно правилу произведения число всевозможных двузначных чисел, составленных с помощью предложенных цифр, равно .

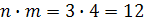Ответ: 12 чисел.

Пример 2. Сколькими способами можно положить 6 различных открыток в 6 имеющихся конвертов (по одной открытке в конверт)?

Решение. Задача сводится к нахождению числа перестановок из 6 элементов. По формуле (1) находим: .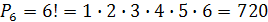

Ответ: 720 способами.

Пример 3. Сколько существует способов выбора двух карт из колоды в 36 карт?

Решение. Изымаемые из колоды всевозможные пары карт без учёта порядка их расположения в наборе образуют сочетания из 36 по 2. По формуле (4) находим

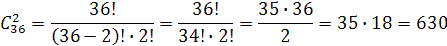
Ответ: 630 способов.

Задания к практической работе

Задание 1. Сколько различных двузначных чисел с разными цифрами можно записать, используя цифры:

1) 1, 2 и 3;

2) 4, 5 и 6;

4) 6, 7, 8 и 9;

6) 0, 3, 5 и 7?

Задание 2. Сколько различных трёхзначных чисел, не имеющих одинаковых цифр, можно записать с помощью цифр:

1) 3, 4 и 5;

2) 7, 8 и 9;

3) 5, б, 7 и 8;

4) 1, 2, 3 и 4?

Задание 3. Сколько различных четырёхбуквенных слов можно записать с помощью букв:

1) «м» и «а»;

2) «п» и «а»;

3) «к», «а» и «о»;

4) «ш», «а» и «л»?

Задание 4. Путешественник может попасть из пункта А в пункт С, проехав через пункт В. Между пунктами А и В имеются три различные дороги, а между пунктами В и С - четыре различные дороги. Сколько существует различных маршрутов между пунктами А и С?

Задание 5. Сколькими способами могут распределиться золотая и серебряная медали на чемпионате по футболу, если в нём принимают участие 32 команды?

Задание 6. Сколькими способами можно составить расписание 5 уроков на один день из 5 различных учебных предметов?

Задание 7. Сколькими способами могут занять очередь в школьный буфет:

1) 6 учащихся;

2) 5 учащихся?

Задание 8. Сколько различных шифров можно набрать в автоматической камере хранения, если шифр составляется с помощью любой из 10 гласных букв с последующим трёхзначным числовым кодом?

Задание 9. Найти значение:

1) ;

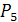2) ;

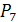3) ;

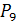4) .

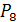Задание 10. Сколько различных пятизначных чисел, не содержащих одинаковых цифр, можно записать с помощью цифр 1, 2, 3, 4, 5 так, чтобы:

1) первой была цифра 5, а второй - цифра 1;

2) последними были цифры 1 и 2, расположенные в любом порядке?

Задание 11. Упростить форму записи выражений (полагая, что 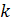- натуральное число, ):

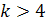1) ;

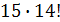2) ;

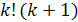3) ;

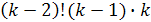4) ;

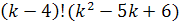Задание 12. Найти значения выражения:

1) ;

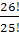2) ;

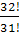3) ;

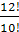4) ;

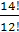5) ;

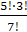6) ;

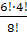7) ;

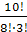8) .

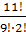Задание 13. Упростить выражение (буквам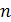и и 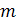обозначены натуральные числа)

1) ;

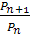2) ;

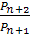3) ;

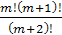4) .

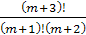Задание 14. Решить уравнение относительно :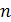

1) ;

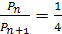2) .

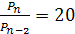Задание 15. Сколько различных слов можно составить, переставляя местами буквы в слове:

1) гипотенуза;

2) треугольник?

Задание 16. Сколько различных шестизначных чисел, не содержащих одинаковых цифр и кратных 4, можно записать с помощью цифр 1, 3, 5, 6, 7 и 9?

Задание 17. В классе изучают 8 предметов естественно-математического цикла. Сколькими способами можно составить расписание на пятницу, если в этот день должны быть:

1) 5 уроков из пяти разных предметов этого цикла;

2) 6 уроков из шести разных предметов этого цикла.

Задание 18. Сколько существует способов для обозначения с помощью букв А, В, С, D, Е, F вершин данного:

1) четырёхугольника;

2) треугольника?

Задание 19. В классе 20 человек. Сколькими способами из их числа можно сделать назначение: 1) физорга и культорга; 2) физорга, культорга и казначея?

Задание 20. Найти значение выражения:

1) ;

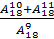2) ;

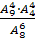Задание 21. Решить относительно 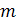уравнение:

1) ;

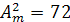2) ;

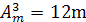3) ;

4) .

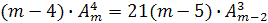Задание 22. Сколькими способами для участия в конференции из 9 членов научного общества можно выбрать:

1) троих студентов;

2) четверых студентов?

Задание 23. В помещении 16 ламп. Сколько существует вариантов его освещения, если одновременно должны светиться:

1) 15 ламп;

2) 14 ламп?

Задание 24. На плоскости отмечено: 1) 16 точек; 2) 13 точек, причём никакие 3 из них не лежат на одной прямой. Сколько различных отрезков можно построить, соединяя эти точки попарно?

Задание 25. В школьном хоре 7 девочек и 4 мальчика. Сколькими способами из состава хора можно выбрать для участия в районном смотре:

1) 5 девочек и 2 мальчиков;

2) 4 девочек и 3 мальчиков?

Задание 26. Найти значение выражения, предварительно его упростив:

1) ;

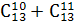2) ;

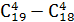3) ;

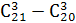4) .

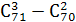Задание 27. Решить уравнение:

1) ;

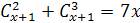2) ;

3) ;

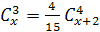4) .

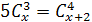Контрольные вопросы:

1. Что называют перестановками из 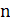элементов. Приведите примеры.

2. Что называют размещениями из 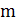элементов по 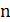элементов. Приведите примеры.

3. Что называют сочетаниями из 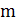элементов по 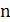элементов. Приведите примеры.

Рекомендуемая литература: 1.1.

СПИСОК ЛИТЕРАТУРЫ

1. Основная:

1.1 Кремер, Н. Ш. Математика для колледжей : учебное пособие для

СПО / Н. Ш. Кремер, О. Г. Константинова, М. Н. Фридман ; под ред. Н. Ш. Кремера. — 10-е изд., перераб. и доп. — М. : Издательство Юрайт, 2018. — 346 с.

1.2 Богомолов, Н. В. Практические занятия по математике в 2 ч. Часть 1 : учебное пособие для СПО / Н. В. Богомолов. — 11-е изд., перераб. и доп. — М. : Издательство Юрайт, 2018. — 285 с.

1.3 Богомолов, Н. В. Практические занятия по математике в 2 ч. Часть 2 : учебное пособие для СПО / Н. В. Богомолов. — 11-е изд., перераб. и доп. — М. : Издательство Юрайт, 2018. — 217 с.

1.4 Богомолов, Н. В. Алгебра и начала анализа : учебное пособие для СПО / Н. В. Богомолов. — М. : Издательство Юрайт, 2018. — 200 с.

1.5 Далингер, В. А. Методика обучения стереометрии посредством решения задач : учебное пособие для СПО / В. А. Далингер. — 2-е изд., испр. и доп. — М. : Издательство Юрайт, 2018. — 370 с.

2. Дополнительная:

2.1 Шипачев, В. С. Математика : учебник и практикум для СПО / В. С. Шипачев ; под ред. А. Н. Тихонова. — 8-е изд., перераб. и доп. — М. : Издательство Юрайт, 2017. — 447 с.

2.2 Кремер, Н. Ш. Теория вероятностей и математическая статистика : учебник и практикум для академического бакалавриата / Н. Ш. Кремер. — 4-е изд., перераб. и доп. — М. : Издательство Юрайт, 2017. — 514 с.

Учебное издание

ОУДп.01 МАТЕМАТИКА: АЛГЕБРА, НАЧАЛА

Дата: 2018-12-28, просмотров: 443.

12 3 4 5 Следующая ⇒